http://poj.org/problem?id=3285
题目大意:
给定一平面上三个圆,设平面上的一个点引到某个圆的两条外切线,两线夹角即为该点对该圆的视角。求平面内的一个点使得三个圆的视角一样大。若存在多个可行解,则取使视角最大的点。
解析:
如果存在可行解,则视角最大的那个点一定在三个圆中间的区域。(肯定存在解,因为一定存在点在无穷远的地方,该点对三个圆的视角都为0)
计算视角:
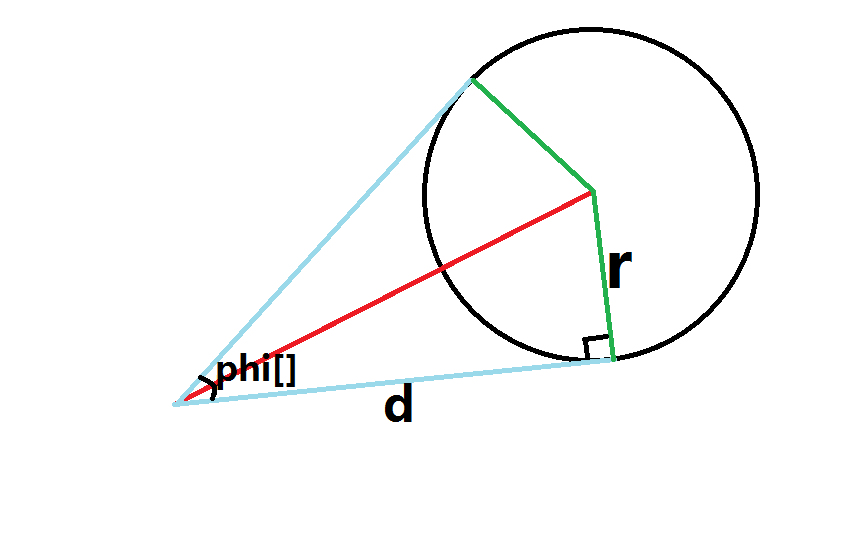
在下面代码中,计算视角是只求tan(phi[]/2)= r / d
计算方差:
在统计学中,方差是表示与均值的偏离程度,这里用方差来计算三个圆的视角的大小相差程度:
((phi[0]*avg)^2 + (phi[1]*avg)^2 + (phi[2]*avg)^2)/ 3
源代码如下:(代码来自duolon)
01 #include <cstdio>
02 #include <cmath>
03 #include <algorithm>
04 #include <ctime>
05 #include <cstdlib>
06 using namespace std;
07
08 const double eps = 1e-8;
09 double x[3], y[3], r[3];
10 double L, R, U, D;
11
12 inline double sqr(double x)
13 {
14 return x * x;
15 }
16 inline double dis(double sx, double sy, int idx)
17 {
18 return sqrt(sqr(sx-x[idx]) + sqr(sy-y[idx]));
19 }
20 inline double calcE(double sx, double sy)
21 {
22 if (sx < L || sx > R) return 1e10;
23 if (sy > U || sy < D) return 1e10;
24 double phi[3];
25 for (int i = 0; i < 3; i++)
26 phi[i] = r[i] / dis(sx,sy,i);
27 double avg = (phi[0]+phi[1]+phi[2])/3;
28 return (sqr(phi[0] - avg) + sqr(phi[1] - avg) + sqr(phi[2] - avg))/3;
29 }
30 int main()
31 {
32 while (true)
33 {
34 bool flag = true;
35 for (int i = 0; i < 3; i++)
36 {
37 scanf("%lf%lf%lf", &x[i], &y[i], &r[i]);
38 if (x[i] != 0 || y[i] != 0 || r[i] != 0) flag = false;
39 }
40 if (flag) break;
41
42 double sx = (x[0]+x[1]+x[2]) / 3;
43 double sy = (y[0]+y[1]+y[2]) / 3;
44 L = min(min(x[0], x[1]), x[2]);
45 R = max(max(x[0], x[1]), x[2]);
46 U = max(max(y[0], y[1]), y[2]);
47 D = min(min(y[0], y[1]), y[2]);
48 double t = max(R-L, U-D);
49 double e = calcE(sx, sy);
50 srand(time(NULL));
51 while (t > eps)
52 {
53 for (int i = 0; i < 20; i++)
54 {
55 double delta = rand();
56 double dx = cos(delta) * t;
57 double dy = sin(delta) * t;
58 double ne = calcE(sx+dx, sy+dy);
59 if (ne < e)
60 sx += dx, sy += dy, e = ne;
61 }
62 t *= 0.88;
63 }
64 if (e < eps)
65 printf("%.2f %.2f\n", sx, sy);
66 else
67 printf("No solution\n");
68 }
69 }
由此题可大致了解模拟退火:
1、 初始几组解:一组
double sx = (x[0]+x[1]+x[2]) / 3;
double sy = (y[0]+y[1]+y[2]) / 3;
在某些题中,可以初始好几组解,然后并行退火,最后得到的几个解中取最优的。如下面那题。
2、 同一温度下移动的步数:在步长为t的情况下,每次向周围随机试走20次
for (int i = 0; i < 20; i++) (源代码中第53行)
{ …… }
3、 退火进度:每次t缩小为88%
t *= 0.88;
PS:因为退火是通过随机来求最优解的,所以在同一温度下要移动的步数和退火的进度只能看rp了,移动步数太少或退火进度太快会使得到的解与最优解差距很大,可能会导致WA;移动步数太多或退火进度太慢又会浪费时间,可能会导致TLE~~
总而言之言而总之模拟退火就是在WA跟TLE之间测试你的rp啦~~
继续PS:据某人说,退火进度通常在0.7~0.9之间能找到~~~至于为什么用0.88,呃,意头好嘛~~