一道几何题,解决方法很容易想到,不过要细心。
随着输入的顺序,将矩形一个个放入集合,如果新的矩形与集合中的旧矩形相交,就将旧矩形分解,删除旧矩形,放入新矩形和分解的矩形。
设矩形R1、R2,宽和高分别为(W1, H1)和(W2, H2),两矩形中心坐标分别为(X1, Y1)以及(X2, Y2)。判断两矩形是否相交(也就是是否有面积相重合),就看两矩形中心坐标的竖直和水平距离是否小于两矩形高的和的一半以及两矩形宽的和的一半。即:
( |X1 - X2| < (W1 + W2) / 2 ) && ( |Y1 - Y2| < (H1 + H2) / 2 )
如果条件满足,R1和R2即相交。
那相交会有几种情况呢?我想到了16种:
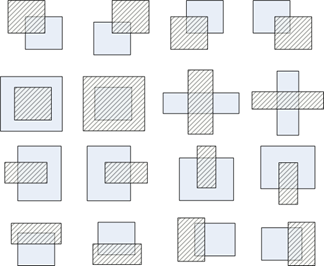
根据不同的情况,可以将原来的矩形分解为0~4个小矩形,这样就可以解出来了。
(做几何题可真费草稿纸啊,看来以后得学学matlab了,低碳、环保!)
另外,USACO还有一种解法,就是将矩形的四条边进行离散化处理,将线段排序,然后再依次扫描,大体思路是这样的,具体细节没怎么看。