http://acm.hdu.edu.cn/showproblem.php?pid=3918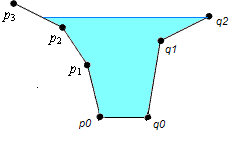



一个如上图所示的杯子，一开始为空，且杯子的重量不计，沿着杯壁往里面慢慢地倒水，直到杯子倒了为止，最高能往里面倒多少水，求最后水的高度。
做法：将杯身分割成梯形，每个梯形中，重心是在x轴的分量，是往一个方向偏移，也就是有单调性。求出从下往上枚举每个梯形，求出第一个使得杯子倒掉的梯形，然后在这个梯形内部二分，求出水的最高位置
  1/*
  2    author: AmazingCaddy
  3    time:    2011-08-04 15:25:53 
  4*/
  5#include <iostream>
  6#include <cstdio>
  7#include <cstring>
  8#include <string>
  9#include <vector>
 10#include <algorithm>
 11#include <stack>
 12#include <queue>
 13#include <complex>
 14#include <cstdlib>
 15#include <cmath>
 16#include <ctime>
 17#include <map>
 18using namespace std;
 19
 20const int maxn = 204;
 21const int inf = 0x3fffffff;
 22const double eps = 1e-8;
 23const double pi = acos( -1.0 );
 24
 25int D( double x ){ return ( x < -eps ? -1 : x > eps ); }
 26
 27struct point
 28{
 29    double x, y;
 30    point( ){ }
 31    point( double _x, double _y ) : x( _x ), y( _y ) { }
 32    void input( ) { scanf( "%lf%lf", &x, &y ); }
 33};
 34
 35point p[ maxn ], q[ maxn ];
 36double Y[ maxn << 1 ];
 37
 38double mass, ypre, ynow;
 39double x1, x2, x3, x4, Gx, LGx;
 40int pid, qid;
 41
 42int myUnique( int n )
 43{
 44    int len = 1;
 45    for( int i = 1; i < n; i++ )
 46        if( D( Y[ i ] - Y[ i - 1 ] ) != 0 )
 47            Y[ len++ ] = Y[ i ];
 48    return len;
 49}
 50
 51double insection( double y, const point &a, const point &b )
 52{
 53    return ( b.x - a.x ) * ( y - a.y ) / ( b.y - a.y ) + a.x;
 54}
 55
 56double get_Gx( double y )
 57{
 58    x3 = insection( y, p[ pid - 1 ], p[ pid ] );
 59    x4 = insection( y, q[ qid - 1 ], q[ qid ] );
 60    double tmp = ( ( x1 + x2 + x3 ) * ( x2 - x1 ) + ( x2 + x4 + x3 ) * ( x4 - x3 ) ) * ( y - ypre ) / 6;
 61    tmp = ( tmp + LGx * mass );
 62    return tmp / ( mass + ( x2 - x1 + x4 - x3 ) * ( y - ypre ) / 2 );
 63}
 64
 65
 66int main(int argc, char *argv[])
 67{
 68//    freopen( "data.in", "r", stdin );
 69//    freopen( "out", "w", stdout );
 70    int cas, n, m;
 71    scanf( "%d", &cas );
 72    while( cas-- )
 73    {
 74        scanf( "%d%d", &m, &n );
 75        for( int i = 0; i < m; i++ )
 76        {
 77            p[ i ].input( );
 78            Y[ i ] = p[ i ].y;
 79        }
 80        for( int j = 0; j < n; j++ )
 81        {
 82            q[ j ].input( );
 83            Y[ j + m ] = q[ j ].y;
 84        }
 85        double ans = min( p[ m - 1 ].y, q[ n - 1 ].y );
 86
 87        sort( Y, Y + m + n );
 88        int len = myUnique( m + n );
 89
 90        pid = 1, qid = 1;
 91
 92        x1 = p[ 0 ].x, x2 = q[ 0 ].x;
 93        mass = 0, LGx = 0, ypre = 0;
 94
 95        for( int i = 1; i < len && D( Y[ i ] - ans ) <= 0; i++ )
 96        {
 97            ynow = Y[ i ];
 98            while( D( p[ pid ].y - ynow ) < 0 ) pid++;
 99            while( D( q[ qid ].y - ynow ) < 0 ) qid++;
100
101            Gx = get_Gx( ynow );
102//            printf( "Gx = %.3lf\n" );
103            if( D( Gx - p[ 0 ].x ) < 0 || D( Gx - q[ 0 ].x ) > 0 )
104            {
105                double l = ypre, r = ynow, mid;
106                while( r - l > eps )
107                {
108                    mid = ( l + r ) * 0.5;
109                    double gx = get_Gx( mid );
110                    if( D( gx - p[ 0 ].x ) < 0 || D( gx - q[ 0 ].x ) > 0 ) r = mid;
111                    else l = mid;
112                }
113                ans = mid;
114                break;
115            }
116
117            mass = mass + ( x2 - x1 + x4 - x3 ) * ( ynow - ypre ) / 2;
118            x1 = x3;
119            x2 = x4;
120            LGx = Gx;
121            ypre = ynow;
122        }
123        printf( "%.3lf\n", ans );
124    }
125    return 0;
126}
。