1. http://acm.pku.edu.cn/JudgeOnline/problem?id=3207题意:在一个圆圈上顺时针或逆时针排好N个点(0-->N-1),现在要以给定的M组端点画M条曲线段,曲线段可在圆内或圆外,判断是否存在一种画法使得这M条曲线段不相交。 分析:每一条曲线段可置于圆内或圆外。这样可用两个顶点分别表示曲线段的摆放情况,例如(顶点2*i表示第i条曲线段置于圆内,顶点2*i+1表示第i条曲线段置于圆外)。 这样对于如下图的两条曲线段 seg[i]=[a,b],seg[j]= [c,d],seg[i]和seg[j]是不能都置于园内,或都置于圆外的。所以顶点2*i和顶点2*j+1,顶点2*j和顶点2*i+1的真值情况必然相同。 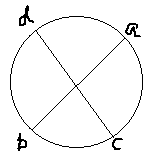 【顺时距离==>用于判断圆内曲线段是否相交】 对于圆内判断是否相交可以这样:如果在a顺时到达b的过程中经过并且只经过了c,d中的一点,那么seg[a,b]和seg[c,d]必然相交。定义顺时距dist[a,b]为a顺时到达b所经过的距离(这个距离可以有几种形式),那么如果 dist[a,c]+dist[c,b]==dist[a,b] 则 “c 在a,b内”,这样如果 c,d中有且只有一点在a,b内,那么seg[a,b]和seg[c,d]必然相交。
  POJ_3207 POJ_3207
1 #include <iostream> #include <iostream>
2 #include <cstring> #include <cstring>
3 #include <cstdio> #include <cstdio>
4 using namespace std; using namespace std;
5
6 const int max_v=1000+5; const int max_v=1000+5;
7 const int max_e=500+5; const int max_e=500+5;
8
9 bool g[max_e*2][max_e*2]; bool g[max_e*2][max_e*2];
10 int N,M; int N,M;
11 int pos[max_e][2],ord[max_e*2],num,col[max_e*2],color; int pos[max_e][2],ord[max_e*2],num,col[max_e*2],color;
12 bool used[max_e*2]; bool used[max_e*2];
13
14  int direc(int u,int p,int v) int direc(int u,int p,int v) { //u顺时针到v是否经过p,如果经过返回1否则返回-1; { //u顺时针到v是否经过p,如果经过返回1否则返回-1;
15 int dist_up=(p>=u)?(p-u):(p-u+N); int dist_pv=(v>=p)?(v-p):(v-p+N); int dist_up=(p>=u)?(p-u):(p-u+N); int dist_pv=(v>=p)?(v-p):(v-p+N);
16 int dist_sum=(v>=u)?(v-u):(v-u+N); int dist_sum=(v>=u)?(v-u):(v-u+N);
17
18 if(dist_up==0||dist_pv==0) return 0; //如果有一个共同点 if(dist_up==0||dist_pv==0) return 0; //如果有一个共同点
19 return (dist_up+dist_pv==dist_sum)?1:-1; return (dist_up+dist_pv==dist_sum)?1:-1;
20 } }
21
22  void back(int v) void back(int v) { {
23 used[v]=true; used[v]=true;
24 col[v]=color; col[v]=color;
25  for(int u=0;u<N;u++) for(int u=0;u<N;u++) { {
26  if(!used[u] && g[u][v]) if(!used[u] && g[u][v]) { {
27 back(u); back(u);
28 } }
29 } }
30 } }
31  void dfs(int u) void dfs(int u) { {
32 used[u]=true; used[u]=true;
33  for(int v=0;v<N;v++) for(int v=0;v<N;v++) { {
34  if(!used[v]&&g[u][v]) if(!used[v]&&g[u][v]) { {
35 dfs(v); dfs(v);
36 } }
37 } }
38 ord[num--]=u; ord[num--]=u;
39 } }
40  int main() int main() { {
41 scanf("%d%d",&N,&M); scanf("%d%d",&N,&M);
42  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
43 scanf("%d%d",&pos[i][0],&pos[i][1]); scanf("%d%d",&pos[i][0],&pos[i][1]);
44 } }
45 memset(g,false,sizeof(g)); memset(g,false,sizeof(g));
46
47  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
48  for(int j=0;j<M;j++) for(int j=0;j<M;j++) { {
49  if(i!=j) if(i!=j) { {
50 int direc1=direc(pos[i][0],pos[j][0],pos[i][1]); int direc1=direc(pos[i][0],pos[j][0],pos[i][1]);
51 int direc2=direc(pos[i][0],pos[j][1],pos[i][1]); int direc2=direc(pos[i][0],pos[j][1],pos[i][1]);
52  if(direc1*direc2==-1) if(direc1*direc2==-1) { {
53 g[2*i][2*j+1]=g[2*j+1][2*i]=true; g[2*i][2*j+1]=g[2*j+1][2*i]=true;
54 g[2*j][2*i+1]=g[2*i+1][2*j]=true; g[2*j][2*i+1]=g[2*i+1][2*j]=true;
55 } }
56 } }
57 } }
58 } }
59
60 N=M*2; num=M*2-1; N=M*2; num=M*2-1;
61
62 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
63 for(int i=0;i<N;i++) if(!used[i]) dfs(i); for(int i=0;i<N;i++) if(!used[i]) dfs(i);
64 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
65 color=0; color=0;
66  for(int i=0;i<N;i++) if(!used[ord[i]]) for(int i=0;i<N;i++) if(!used[ord[i]]) { {
67 back(ord[i]); ++color; back(ord[i]); ++color;
68 } }
69
70  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
71  if(col[2*i]==col[2*i+1]) if(col[2*i]==col[2*i+1]) { {
72 printf("the evil panda is lying again\n"); printf("the evil panda is lying again\n");
73 return 0; return 0;
74 } }
75 } }
76 printf("panda is telling the truth...\n"); printf("panda is telling the truth...\n");
77 return 0; return 0;
78 } }另外此题是判定能否将曲线段划分到两个集合中。可以用并查集来写
  POJ_3207 POJ_3207
1 #include <iostream> #include <iostream>
2 #include <cstring> #include <cstring>
3 #include <cstdio> #include <cstdio>
4 using namespace std; using namespace std;
5
6 const int max_v=1000+5; const int max_v=1000+5;
7 const int max_e=500+5; const int max_e=500+5;
8
9
10 int N,M; int N,M;
11 int pos[max_e][2]; int pos[max_e][2];
12 int pnt[max_e]; int pnt[max_e];
13 int ct[max_e]; int ct[max_e];
14
15  int direc(int u,int p,int v) int direc(int u,int p,int v) { //u顺时针到v是否经过p,如果经过返回1否则返回-1; { //u顺时针到v是否经过p,如果经过返回1否则返回-1;
16 int dist_up=(p>=u)?(p-u):(p-u+N); int dist_pv=(v>=p)?(v-p):(v-p+N); int dist_up=(p>=u)?(p-u):(p-u+N); int dist_pv=(v>=p)?(v-p):(v-p+N);
17 int dist_sum=(v>=u)?(v-u):(v-u+N); int dist_sum=(v>=u)?(v-u):(v-u+N);
18
19 if(dist_up==0||dist_pv==0) return 0; //如果有一个共同点 if(dist_up==0||dist_pv==0) return 0; //如果有一个共同点
20 return (dist_up+dist_pv==dist_sum)?1:-1; return (dist_up+dist_pv==dist_sum)?1:-1;
21 } }
22
23  int findSet(int u) int findSet(int u) { {
24 if(pnt[u]<0) return u; if(pnt[u]<0) return u;
25
26 int tmp=pnt[u]; int tmp=pnt[u];
27 pnt[u]=findSet(pnt[u]); pnt[u]=findSet(pnt[u]);
28 ct[u]=(ct[u]+ct[tmp])%2; ct[u]=(ct[u]+ct[tmp])%2;
29
30 return pnt[u]; //It's pnt[u],but not tmp! return pnt[u]; //It's pnt[u],but not tmp!
31 } }
32
33  void unionSet(int u,int v) void unionSet(int u,int v) { {
34 int pv=findSet(v),pu=findSet(u); int pv=findSet(v),pu=findSet(u);
35 pnt[pu]=pv; pnt[pu]=pv;
36 ct[pu]=(ct[v]-ct[u]+3)%2; ct[pu]=(ct[v]-ct[u]+3)%2;
37 } }
38  int main() int main() { {
39 scanf("%d%d",&N,&M); scanf("%d%d",&N,&M);
40  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
41 scanf("%d%d",&pos[i][0],&pos[i][1]); scanf("%d%d",&pos[i][0],&pos[i][1]);
42 } }
43
44 memset(pnt,-1,sizeof(pnt)); memset(pnt,-1,sizeof(pnt));
45 memset(ct,0,sizeof(ct)); memset(ct,0,sizeof(ct));
46
47  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
48  for(int j=i+1;j<M;j++) for(int j=i+1;j<M;j++) { {
49 int direc1=direc(pos[i][0],pos[j][0],pos[i][1]); int direc1=direc(pos[i][0],pos[j][0],pos[i][1]);
50 int direc2=direc(pos[i][0],pos[j][1],pos[i][1]); int direc2=direc(pos[i][0],pos[j][1],pos[i][1]);
51  if(direc1*direc2==-1) if(direc1*direc2==-1) { {
52 int pi=findSet(i),pj=findSet(j); int pi=findSet(i),pj=findSet(j);
53  if(pi==pj && ct[i]!=(ct[j]^1)) if(pi==pj && ct[i]!=(ct[j]^1)) { {
54 printf("the evil panda is lying again\n"); printf("the evil panda is lying again\n");
55 return 0; return 0;
56  }else if(pi!=pj) }else if(pi!=pj) { {
57 unionSet(i,j); unionSet(i,j);
58 } }
59 } }
60 } }
61 } }
62 printf("panda is telling the truth printf("panda is telling the truth \n"); \n");
63 return 0; return 0;
64 } }
65 2. http://acm.hdu.edu.cn/showproblem.php?pid=3622 (二分答案+2-sat判定)
  HDU_3622_Bomb_Game HDU_3622_Bomb_Game
1 #include <iostream> #include <iostream>
2 #include <cstring> #include <cstring>
3 #include <cstdio> #include <cstdio>
4 #include <cmath> #include <cmath>
5 using namespace std; using namespace std;
6
7 const int max_v=200+5; const int max_v=200+5;
8 bool g[max_v][max_v]; bool g[max_v][max_v];
9 bool used[max_v]; bool used[max_v];
10 int N; int N;
11 int pos[max_v][2]; int pos[max_v][2];
12 double dist[max_v][max_v]; double dist[max_v][max_v];
13 int color ,col[max_v],num,ord[max_v]; int color ,col[max_v],num,ord[max_v];
14
15  double cal(int i,int j) double cal(int i,int j) { {
16 double x1=pos[i][0]*1.0,x2=pos[j][0]*1.0,y1=pos[i][1]*1.0,y2=pos[j][1]*1.0; double x1=pos[i][0]*1.0,x2=pos[j][0]*1.0,y1=pos[i][1]*1.0,y2=pos[j][1]*1.0;
17 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
18 } }
19
20  void back(int v) void back(int v) { {
21 used[v]=true; used[v]=true;
22 col[v]=color; col[v]=color;
23  for(int u=0;u<N;u++) for(int u=0;u<N;u++) { {
24  if(!used[u] && g[u][v]) if(!used[u] && g[u][v]) { {
25 back(u); back(u);
26 } }
27 } }
28 } }
29  void dfs(int u) void dfs(int u) { {
30 used[u]=true; used[u]=true;
31  for(int v=0;v<N;v++) for(int v=0;v<N;v++) { {
32  if(!used[v] && g[u][v]) if(!used[v] && g[u][v]) { {
33 dfs(v); dfs(v);
34 } }
35 } }
36 ord[num--]=u; ord[num--]=u;
37 } }
38
39  bool isok(double mid_dist) bool isok(double mid_dist) { {
40
41 memset(g,0,sizeof(g)); memset(g,0,sizeof(g));
42
43  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
44  for(int j=0;j<N;j++) for(int j=0;j<N;j++) { {
45  if((i/2)!=(j/2)) if((i/2)!=(j/2)) { {
46 int ai=((i/2)*4+1)-i, bj=((j/2)*4+1)-j; int ai=((i/2)*4+1)-i, bj=((j/2)*4+1)-j;
47  if(dist[i][j]<mid_dist*2.0) if(dist[i][j]<mid_dist*2.0) { {
48 g[i][bj]=true; g[i][bj]=true;
49 g[j][ai]=true; g[j][ai]=true;
50 } }
51 } }
52 } }
53 } }
54 memset(used,false,sizeof(used)); memset(used,false,sizeof(used));
55 num=N-1; num=N-1;
56 for(int i=0;i<N;i++) if(!used[i]) dfs(i); for(int i=0;i<N;i++) if(!used[i]) dfs(i);
57
58 memset(used,false,sizeof(used)); memset(used,false,sizeof(used));
59 color=0; color=0;
60  for(int j=0;j<N;j++) if(!used[ord[j]]) for(int j=0;j<N;j++) if(!used[ord[j]]) { {
61 ++color; back(ord[j]); ++color; back(ord[j]);
62 } }
63  for(int i=0;i+1<N;i+=2) for(int i=0;i+1<N;i+=2) { {
64  if(col[i]==col[i+1]) if(col[i]==col[i+1]) { {
65 return false; return false;
66 } }
67 } }
68 return true; return true;
69 } }
70
71 int main() int main()
72   { {
73  while(scanf("%d",&N)!=EOF) while(scanf("%d",&N)!=EOF) { {
74 N*=2; N*=2;
75  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
76 scanf("%d%d",&pos[i][0],&pos[i][1]); scanf("%d%d",&pos[i][0],&pos[i][1]);
77 } }
78  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
79  for(int j=i+1;j<N;j++) for(int j=i+1;j<N;j++) { {
80 dist[i][j]=dist[j][i]=cal(i,j); dist[i][j]=dist[j][i]=cal(i,j);
81 } }
82 } }
83
84
85 double lt=0,rt=15000.0; double lt=0,rt=15000.0;
86
87  while(fabs(lt-rt)>(1e-4)) while(fabs(lt-rt)>(1e-4)) { {
88 double mid=(lt+rt)/2.0; double mid=(lt+rt)/2.0;
89  if(isok(mid)) if(isok(mid)) { {
90 lt=mid; lt=mid;
91  }else }else { {
92 rt=mid; rt=mid;
93 } }
94 } }
95 printf("%.2f\n",lt); printf("%.2f\n",lt);
96 } }
97 return 0; return 0;
98 } }
99 3. http://acm.pku.edu.cn/JudgeOnline/problem?id=2723 二分答案 + 2-sat判定。 最开始我构图不够严谨,只是以用了某个钥匙为顶点。然后判断是不是用了某两个属于同一组的钥匙从而判断是否有解。 其实这样是不够的,因为有解的话并不一定要从同一组钥匙中选一个。所以这样转化成2-sat是不行的,应该将用第i类钥匙和不用第i类钥匙作为图的 p 和 ¬p顶点,这样p和¬p必选其一。
  POJ_2723_Get_Luffy_Out POJ_2723_Get_Luffy_Out
1 #include <iostream> #include <iostream>
2 #include <cstdio> #include <cstdio>
3 #include <cstring> #include <cstring>
4
5 using namespace std; using namespace std;
6
7 const int max_v=5000; const int max_v=5000;
8 const int max_e=max_v*max_v*4; const int max_e=max_v*max_v*4;
9
10 int beg[2][max_v],match[max_v],next[2][max_e],v[2][max_e],nedge[2]; int beg[2][max_v],match[max_v],next[2][max_e],v[2][max_e],nedge[2];
11 int ord[max_v],col[max_v],color,num; bool used[max_v]; int ord[max_v],col[max_v],color,num; bool used[max_v];
12 int N,M; int N,M;
13 int pos[max_v*2]; int pos[max_v*2];
14
15  void add_edge(int ut,int vt) void add_edge(int ut,int vt) { {
16 v[0][nedge[0]]=vt; next[0][nedge[0]]=beg[0][ut]; beg[0][ut]=nedge[0]++; v[0][nedge[0]]=vt; next[0][nedge[0]]=beg[0][ut]; beg[0][ut]=nedge[0]++;
17 v[1][nedge[1]]=ut; next[1][nedge[1]]=beg[1][vt]; beg[1][vt]=nedge[1]++; v[1][nedge[1]]=ut; next[1][nedge[1]]=beg[1][vt]; beg[1][vt]=nedge[1]++;
18 } }
19
20  void back(int ep) void back(int ep) { {
21 used[ep]=true; col[ep]=color; used[ep]=true; col[ep]=color;
22  for(int bp=beg[1][ep];bp!=-1;bp=next[1][bp]) for(int bp=beg[1][ep];bp!=-1;bp=next[1][bp]) { {
23 int vt=v[1][bp]; int vt=v[1][bp];
24  if(!used[vt]) if(!used[vt]) { {
25 back(vt); back(vt);
26 } }
27 } }
28 } }
29  void dfs(int bp) void dfs(int bp) { {
30 used[bp]=true; used[bp]=true;
31  for(int ep=beg[0][bp];ep!=-1;ep=next[0][ep]) for(int ep=beg[0][bp];ep!=-1;ep=next[0][ep]) { int vt=v[0][ep]; { int vt=v[0][ep];
32  if(!used[vt]) if(!used[vt]) { {
33 dfs(vt); dfs(vt);
34 } }
35 } }
36 ord[num--]=bp; ord[num--]=bp;
37 } }
38  bool isok(int T) bool isok(int T) { {
39 memset(beg,-1,sizeof(beg)); nedge[0]=nedge[1]=0; memset(beg,-1,sizeof(beg)); nedge[0]=nedge[1]=0;
40
41  for(int i=0;i<2*N;i++) for(int i=0;i<2*N;i++) { {
42  if(i<match[i]) if(i<match[i]) { {
43 add_edge(2*i,2*match[i]+1); //用i就不用match[i]; add_edge(2*i,2*match[i]+1); //用i就不用match[i];
44 add_edge(2*match[i],2*i+1); //用match[i]就不用i; add_edge(2*match[i],2*i+1); //用match[i]就不用i;
45 } }
46 } }
47  for(int i=0;i+1<2*T;i+=2) for(int i=0;i+1<2*T;i+=2) { //要打开第i扇门,至少用这一组钥匙中的一个。 { //要打开第i扇门,至少用这一组钥匙中的一个。
48 add_edge(2*pos[i]+1,2*pos[i+1]); add_edge(2*pos[i]+1,2*pos[i+1]);
49 add_edge(2*pos[i+1]+1,2*pos[i]); add_edge(2*pos[i+1]+1,2*pos[i]);
50 } }
51  for(int i=0;i<2*T;i++) for(int i=0;i<2*T;i++) { {
52  for(int j=i+1;j<2*T;j++) for(int j=i+1;j<2*T;j++) { {
53  if((i/2)!=(j/2) && match[pos[i]]==pos[j]) if((i/2)!=(j/2) && match[pos[i]]==pos[j]) {//不同的两条门中有两个钥匙属于同一组 {//不同的两条门中有两个钥匙属于同一组
54 int partner_i=((i/2)*4+1)-i,partner_j=((j/2)*4+1)-j; int partner_i=((i/2)*4+1)-i,partner_j=((j/2)*4+1)-j;
55 add_edge(2*pos[i],2*pos[partner_j]); //用pos[i]就必须用pos[partner_j]; add_edge(2*pos[i],2*pos[partner_j]); //用pos[i]就必须用pos[partner_j];
56 add_edge(2*pos[j],2*pos[partner_i]); //用pos[j]就必须用pos[partner_i]; add_edge(2*pos[j],2*pos[partner_i]); //用pos[j]就必须用pos[partner_i];
57 } }
58 } }
59 } }
60 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
61 num=4*N-1; num=4*N-1;
62  for(int i=0;i<4*N;i++) for(int i=0;i<4*N;i++) { {
63 if(!used[i]) dfs(i); if(!used[i]) dfs(i);
64 } }
65 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
66 color=0; color=0;
67  for(int i=0;i<4*N;i++) for(int i=0;i<4*N;i++) { {
68  if(!used[ord[i]]) if(!used[ord[i]]) { {
69 color++; back(ord[i]); color++; back(ord[i]);
70 } }
71 } }
72  for(int i=0;2*i+1<4*N;i+=2) for(int i=0;2*i+1<4*N;i+=2) { //不能既用i又不用i { //不能既用i又不用i
73  if(col[2*i]==col[2*i+1]) if(col[2*i]==col[2*i+1]) { {
74 return false; return false;
75 } }
76 } }
77 return true; return true;
78 } }
79
80 int main() int main()
81   { {
82  while(scanf("%d%d",&N,&M),(N+M)) while(scanf("%d%d",&N,&M),(N+M)) { {
83 int ut,vt; int ut,vt;
84  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
85 scanf("%d%d",&ut,&vt); scanf("%d%d",&ut,&vt);
86 match[ut]=vt; match[vt]=ut; match[ut]=vt; match[vt]=ut;
87 } }
88  for(int i=0;i<M;i++) for(int i=0;i<M;i++) { {
89 scanf("%d%d",&pos[2*i],&pos[2*i+1]); scanf("%d%d",&pos[2*i],&pos[2*i+1]);
90 } }
91 int lt=1,rt=M; int lt=1,rt=M;
92  while(lt<=rt) while(lt<=rt) { {
93 int mid=(lt+rt)/2; int mid=(lt+rt)/2;
94  if(isok(mid)) if(isok(mid)) { {
95 lt=mid+1; lt=mid+1;
96  }else }else { {
97 rt=mid-1; rt=mid-1;
98 } }
99 } }
100 printf("%d\n",rt); printf("%d\n",rt);
101 } }
102
103 return 0; return 0;
104 } }
105
4. http://acm.pku.edu.cn/JudgeOnline/problem?id=2749 (二分+ 2SAT) 牛i 连S1和S2分别为顶点Pi 和¬Pi之后二分就行 (第一次WA后发现没用memcpy将信息备份那个nedge一直在增加,第二次WA后发现竟然将enemy和friend的输入顺序搞反了,太没素质了。悲剧)。
  POJ_2749_Building roads POJ_2749_Building roads
1 #include <iostream> #include <iostream>
2 #include <cstdio> #include <cstdio>
3 #include <cstring> #include <cstring>
4 using namespace std; using namespace std;
5
6 const int max_v=2000+5; const int max_v=2000+5;
7 const int max_e=max_v*max_v*4; const int max_e=max_v*max_v*4;
8 int coord[max_v][2]; int coord[max_v][2];
9 int s[2][2]; int s[2][2];
10 int beg[2][max_v],next[2][max_e],v[2][max_e],nedge[2]; int beg[2][max_v],next[2][max_e],v[2][max_e],nedge[2];
11 int beg_backup[2][max_v],nedge_backup[2]; int beg_backup[2][max_v],nedge_backup[2];
12 bool used[max_v]; int ord[max_v],num,col[max_v],color; bool used[max_v]; int ord[max_v],num,col[max_v],color;
13 int dist[max_v],dist_s1_s2; int dist[max_v],dist_s1_s2;
14 int N,M,K; int N,M,K;
15
16  int cal(int a[],int b[]) int cal(int a[],int b[]) { {
17 return abs(a[0]-b[0])+abs(a[1]-b[1]); return abs(a[0]-b[0])+abs(a[1]-b[1]);
18 } }
19
20  void back(int ep) void back(int ep) { {
21 used[ep]=true; col[ep]=color; used[ep]=true; col[ep]=color;
22  for(int i=beg[1][ep];i!=-1;i=next[1][i]) for(int i=beg[1][ep];i!=-1;i=next[1][i]) { int vt=v[1][i]; { int vt=v[1][i];
23  if(!used[vt]) if(!used[vt]) { {
24 back(vt); back(vt);
25 } }
26 } }
27 } }
28  void dfs(int bp) void dfs(int bp) { {
29 used[bp]=true; used[bp]=true;
30  for(int i=beg[0][bp];i!=-1;i=next[0][i]) for(int i=beg[0][bp];i!=-1;i=next[0][i]) { int vt=v[0][i]; { int vt=v[0][i];
31  if(!used[vt]) if(!used[vt]) { {
32 dfs(vt); dfs(vt);
33 } }
34 } }
35 ord[num--]=bp; ord[num--]=bp;
36 } }
37
38
39  void add_edge(int ut,int vt) void add_edge(int ut,int vt) { {
40 v[0][nedge[0]]=vt; next[0][nedge[0]]=beg[0][ut]; beg[0][ut]=nedge[0]++; v[0][nedge[0]]=vt; next[0][nedge[0]]=beg[0][ut]; beg[0][ut]=nedge[0]++;
41 v[1][nedge[1]]=ut; next[1][nedge[1]]=beg[1][vt]; beg[1][vt]=nedge[1]++; v[1][nedge[1]]=ut; next[1][nedge[1]]=beg[1][vt]; beg[1][vt]=nedge[1]++;
42 } }
43
44  bool isok(int mid_dist) bool isok(int mid_dist) { {
45
46 memcpy(beg,beg_backup,sizeof(beg)); memcpy(nedge,nedge_backup,sizeof(nedge)); memcpy(beg,beg_backup,sizeof(beg)); memcpy(nedge,nedge_backup,sizeof(nedge));
47  for(int i=0;i<2*N;i++) for(int i=0;i<2*N;i++) { {
48  for(int j=i+1;j<2*N;j++) for(int j=i+1;j<2*N;j++) { {
49  if((i/2)!=(j/2)) if((i/2)!=(j/2)) { {
50 int part_i=((i/2)*4)+1-i,part_j=((j/2)*4)+1-j; int part_i=((i/2)*4)+1-i,part_j=((j/2)*4)+1-j;
51
52  if( (i+j)%2==0 && dist[i]+dist[j]>mid_dist) if( (i+j)%2==0 && dist[i]+dist[j]>mid_dist) {//同一个节点 {//同一个节点
53 add_edge(i,part_j); add_edge(j,part_i); add_edge(i,part_j); add_edge(j,part_i);
54  }else if( (i+j)%2 && dist[i]+dist[j]+dist_s1_s2>mid_dist) }else if( (i+j)%2 && dist[i]+dist[j]+dist_s1_s2>mid_dist) { {
55 add_edge(i,part_j); add_edge(j,part_i); add_edge(i,part_j); add_edge(j,part_i);
56 } }
57 } }
58 } }
59 } }
60
61 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
62 num=2*N-1; num=2*N-1;
63  for(int i=0;i<2*N;i++) for(int i=0;i<2*N;i++) { {
64 if(!used[i]) dfs(i); if(!used[i]) dfs(i);
65 } }
66
67 memset(used,0,sizeof(used)); memset(used,0,sizeof(used));
68 color=0; color=0;
69
70  for(int i=0;i<2*N;i++) for(int i=0;i<2*N;i++) { {
71  if(!used[ord[i]]) if(!used[ord[i]]) { {
72 color++; back(ord[i]); color++; back(ord[i]);
73 } }
74 } }
75
76  for(int i=0;i+1<2*N;i+=2) for(int i=0;i+1<2*N;i+=2) { {
77 if(col[i]==col[i+1]) return false; if(col[i]==col[i+1]) return false;
78 } }
79
80 return true; return true;
81 } }
82 int main() int main()
83   { {
84 // freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); // freopen("in.txt","r",stdin); freopen("out.txt","w",stdout);
85  while(scanf("%d%d%d",&N,&M,&K)!=EOF) while(scanf("%d%d%d",&N,&M,&K)!=EOF) { {
86
87 scanf("%d%d%d%d",&s[0][0],&s[0][1],&s[1][0],&s[1][1]); scanf("%d%d%d%d",&s[0][0],&s[0][1],&s[1][0],&s[1][1]);
88 dist_s1_s2=cal(s[0],s[1]); dist_s1_s2=cal(s[0],s[1]);
89
90  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
91 scanf("%d%d",&coord[i][0],&coord[i][1]); scanf("%d%d",&coord[i][0],&coord[i][1]);
92 } }
93 int ut,vt; int ut,vt;
94 memset(beg,-1,sizeof(beg)); memset(beg,-1,sizeof(beg));
95 nedge[0]=nedge[1]=0; nedge[0]=nedge[1]=0;
96  for(int i=0;i<M;i++) for(int i=0;i<M;i++) {//连接不同节点 {//连接不同节点
97 scanf("%d%d",&ut,&vt); scanf("%d%d",&ut,&vt);
98 ut--; vt--; ut--; vt--;
99 add_edge(ut*2,vt*2+1); add_edge(ut*2+1,vt*2); add_edge(ut*2,vt*2+1); add_edge(ut*2+1,vt*2);
100 add_edge(vt*2,ut*2+1); add_edge(vt*2+1,ut*2); add_edge(vt*2,ut*2+1); add_edge(vt*2+1,ut*2);
101 } }
102
103  for(int i=0;i<K;i++) for(int i=0;i<K;i++) {//ut,vt连通一个节点 {//ut,vt连通一个节点
104 scanf("%d%d",&ut,&vt); scanf("%d%d",&ut,&vt);
105 ut--; vt--; ut--; vt--;
106 add_edge(ut*2,vt*2); add_edge(vt*2,ut*2); //同为S1 add_edge(ut*2,vt*2); add_edge(vt*2,ut*2); //同为S1
107 add_edge(ut*2+1,vt*2+1); add_edge(vt*2+1,ut*2+1); //同为S2 add_edge(ut*2+1,vt*2+1); add_edge(vt*2+1,ut*2+1); //同为S2
108 } }
109
110 memcpy(beg_backup,beg,sizeof(beg)); memcpy(nedge_backup,nedge,sizeof(nedge)); memcpy(beg_backup,beg,sizeof(beg)); memcpy(nedge_backup,nedge,sizeof(nedge));
111
112 int max_dist=dist_s1_s2,min_dist=(1<<30); int max_dist=dist_s1_s2,min_dist=(1<<30);
113
114  for(int i=0;i<N;i++) for(int i=0;i<N;i++) { {
115 dist[2*i]=cal(coord[i],s[0]); dist[2*i]=cal(coord[i],s[0]);
116 dist[2*i+1]=cal(coord[i],s[1]); dist[2*i+1]=cal(coord[i],s[1]);
117 max_dist=max(max_dist,dist[2*i]); max_dist=max(max_dist,dist[2*i+1]); max_dist=max(max_dist,dist[2*i]); max_dist=max(max_dist,dist[2*i+1]);
118 min_dist=min(min_dist,dist[2*i]); min_dist=min(min_dist,dist[2*i+1]); min_dist=min(min_dist,dist[2*i]); min_dist=min(min_dist,dist[2*i+1]);
119 } }
120
121  if(!isok(1<<30)) if(!isok(1<<30)) { {
122 printf("-1\n"); printf("-1\n");
123 continue; continue;
124 } }
125
126 int lt=min_dist*2,rt=max_dist*3; int lt=min_dist*2,rt=max_dist*3;
127
128  while(lt<=rt) while(lt<=rt) { {
129 int mid=(lt+rt)/2; int mid=(lt+rt)/2;
130  if(isok(mid)) if(isok(mid)) { {
131 rt=mid-1; rt=mid-1;
132  }else }else { {
133 lt=mid+1; lt=mid+1;
134 } }
135 } }
136 printf("%d\n",lt); printf("%d\n",lt);
137 } }
138 return 0; return 0;
139 } }
140

|
|
|
CALENDER
| | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
|---|
| 25 | 26 | 27 | 28 | 29 | 30 | 31 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | | 8 | 9 | 10 | 11 | 12 | 13 | 14 | | 15 | 16 | 17 | 18 | 19 | 20 | 21 | | 22 | 23 | 24 | 25 | 26 | 27 | 28 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
常用链接
留言簿
随笔分类
随笔档案
搜索
最新评论

阅读排行榜
评论排行榜
Powered By: 博客园
模板提供:沪江博客
|