题目链接:
pku_1850_Code_ http://162.105.81.212/JudgeOnline/problem?id=1850
pku_1496_Word Index http://162.105.81.212/JudgeOnline/problem?id=1496
【问题概述】:给定一个长度为N(n<=10)的由小写字母组成的字符串,
如果该字符串左边的字符都比右边的字符的字典序大,则我们称这个字符串是合法的,
否则不合法:
e.g: 字符串:abc ade 是合法的,而字符串:bac bca dae 则是不合法的。
现在对合法的字符串进行如下的编码(编号):
a - 1
b - 2
...
z - 26
ab - 27
...
az - 51
bc - 52
...
vwxyz - 83681
...
我们的任务就是对于给定的字符串,如果她是合法的,则找到她的编号,否则不合法,输出0:
【问题分析】:首先想到的应该是暴力,但是暴力的复杂度会达到O(10^26),可能会超时,当然有人爆过了。
这里将一个更为高效的算法。先看一下这个图: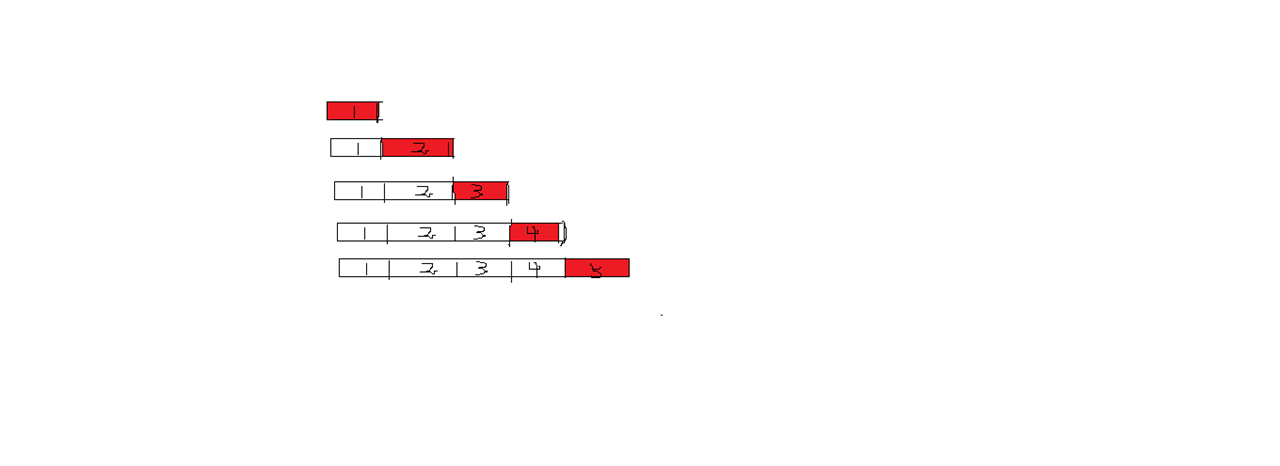
我们可以知道,长度为k(k>=1)的字符串的编号是在长度为k-1的基础上增加而来的,为了计算的方便,我们可以先计算出长度为k-1的字符串可以编号为多少,也就知道了长度为k的第一个字符串的编号(加一就可以)。但是问题还没得到解决,下面是重点:该如何统计当前输入的长度为k的字符串的编号:她等于长度为k-1的最大编号加上当前字符串在当前长度的编号。由此如何快速统计当前字符串在当前长度的集合(把不同的长度的字符串划分为不同的集合)里编号是解决这个题目的第二个要点。
设s[k][i](0< i<= 26)表示长度等于k的合法串以字母(i+'a'-1)开头的串的数目,则规定s[k][26]表示长度为k的集合的合法串的总的个数。对于给定的长度为n的字符串,我们由右向左考虑,找第i个字符和第i-1个字符的关系:令tmp = s[ k ][ str[i] - 1] - s[k][ str[i-1] ],表示在前i-1个字符不变时,可得到的不同的新合法字符串的个数。对于第一个字符,我们要判断她是不是第一个字母‘a',不是的话,她可以得到的心合法字符串的个数为s[k][str[0]-1]. 最后的话,我们再把所有长度小于n的字符长的个数加起来就是我们要求的:下面是简单的代码,供大家讨论交流:
#include <iostream>
#include <string.h>
using namespace std;
const int maxn = 28;
int s[11][maxn], n;
bool isValid(char *s, int &n) {
int i = n = 0;
for(i = 1; s[i]; i++)
if(s[i] <= s[i-1]) return 0;
n = i;
return 1;
}
void init() {
s[0][27] = 1;
for (int k = 1; k < 11; k++) {
int m = 26-k+1;
for (int i = 1; i <= m; i++) {
s[k][i] += s[k][i-1] + s[k-1][m+1]-s[k-1][i];
}
}
s[0][27] = 0;
}
void pt() {
int sum = 0;
for (int k = 1; k < 11; k++) {
int m = 26-k+1;
for (int i = 1; i <= m; i++) {
printf("s[%d][%d] = %d\n", k, i, s[k][i]);
}
sum += s[k][m];
}
printf("%d\n", sum);
}
inline int d(char c) { return c-'a'+1;}
int main() {//freopen("in.in", "r", stdin);
init(); //pt();
char str[11];
int m, i, k;
while(scanf("%s", str) != EOF) {
if (!isValid(str, n)) { puts("0"); continue;}
for (i = n-1, k = 1, m = 1; i >= 1; i--, k++)
m += s[k][d(str[i]-1)] - s[k][d(str[i-1])];
if (str[0] != 'a') m += s[k][d(str[0]-1)];
for (i = 1; i < k; i++) m += s[i][26-i+1];
printf("%d\n", m);
}
return 0;
}