平面点的曼哈顿最小生成树

引言

作者阅读并研究了由Hai Zhou (Electrical and Computer Engineering, Northwestern University, Evanston, IL 60208, USA)，Narendra Shenoy和William Nicholls (Advanced Technology Group, Synopsys, Inc., Mountain View, CA 94043, USA)撰写的论文《Efficient minimum spanning tree construction without Delaunay triangulation》，现将一些收获体会总结如下。

问题描述

平面上有n个不重合的点，你的任务是求这些点的最小生成树。两个点(x₀,y₀)和(x₁,y₁)之间的距离定义为|x₀-x₁|+|y₀-y₁|。（即曼哈顿距离）

如果在任意两个点之间都连一条边，边的权值等于两点的曼哈顿距离，那么这个题目就是标准的最小生成树问题。一个包含n个点n²条边的图，求最小生成树的代价是O(n²)。但是这种一般性的做法没有考虑到“平面”的性质。下面将通过分析最小生成树的性质和平面性质的结合，得到一个O(nlogn)的算法。

最小生成树的“环切”性质

先抛开“平面”，我们考虑一般的离散图的最小生成树有什么性质。

环切性质 在图G=(V,E)中，如果存在一个环，把环中权最大的边e删除得到图G’=(V,E\{e})（如果有多条最大边，则删除任意一条），则G和G’的最小生成树权和相同。

证明：

假设e(e∈E)在G的一个环C上，并且是环上的权最大边。

假设G的某棵最小生成树T包含了e，考虑e连接的两个点u和v。把e从T中删除，就把T分成两个连通分量，u,v分处不同的连通分量。在环C上对应的把e删除，从u到v还是有一条通路，并且通路上的所有边权值都不大于e的权值；假设这条通路是(u, x₁, x₂, …, x_L, v)。

在点集S={u, x₁, x₂, …, x_L, v}中，和u属于同一个集合的点称之为红点，和v属于同一个集合的称之为蓝点。显然S中至少有一个红点(u)、至少有一个蓝点(v)。所以在序列(u, x₁, x₂, …, x_L, v)中必然存在相邻的两个点颜色不同，不妨设为a和b。将<a,b>加入到被删除了e的T中，就得到了一棵新的生成树T’：即T’=(T\{e})∪{<a,b>}。前面提到了通路(u, x₁, x₂, …, x_L, v)中任意一条边都不大于e，所以<a,b>的权不大于e的权。即T’也是G的一棵最小生成树。

因为G’是G的子图，所以T’也是G’的最小生成树。而T和T’的权和相等（都是G的最小生成树）。

证毕。

区域分类法

通过最小生成树的“环切”性质，我们可以发现有很多边是没有用的。如果图中存在一个环，那么就至少能删掉一条边而保持最小生成树不变。

我们回到“平面”问题。基本思路还是构建一个离散图——但是这个图的边数必须远远小于n²。换句话说我们要想办法利用“环切”性质，只保留一些有用的边。

考察某个点s。我们从s发出8条射线将平面均分成八个部分：

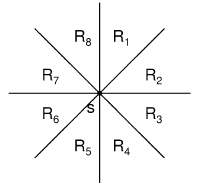
如果点落在射线上，按如下方法划分：

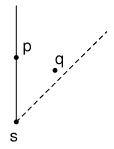
实线上的点属于这个区域、虚线上的点不属于。上图中p, q都属于该区域。

下面我们证明：在每个区域里面，s只要和至多一个点连边即可。

八个扇形区域是对称的，我们只考虑R₁。

把s看作原点，R₁里面的点(x,y)都满足：

x≥0,

y>x.

考察R₁里面两个点p和q，不失一般性设x_p≤x_q。

1.       y_p≤y_q

|PQ|=x_q+y_q-(x_p+x_q)

|SP|=x_p+y_p

|SQ|=x_q+y_q

所以|PQ|=|SQ|-|SP|≤|SQ|

可见当y_p≤y_q时，|PQ|不是三角形SPQ的最长边。（在曼哈顿距离下的“最长”）

2.       y_p>y_q­

0≤x_p≤x_q≤y_q<y_p

|PQ|=x_q-x_p+y_p-y_q

|SP|=x_p+y_p

|SQ|=x_q+y_q

即|PQ|= (y_p-x_p)+(x_q-y_q)

因为x_q≤y_q，所以|PQ|≤yp-xp≤yp≤xp+yp=|SP|

也就是说，当y_p>y_q时，|PQ|仍然不是三角形SPQ的最长边。（曼哈顿距离意义下的“最长”）

综上，|PQ|无论如何也不可能是三角形SPQ的最长边。即：在环<s, p, q>中，最大边只可能是|SP|和|SQ|。根据“环切”性质，我们把|SP|和|SQ|中的较长边删除即可。

假设R₁里面有m个顶点：P₁, P₂, …, P_m，假设距离s最近的点是P_k，那么只要在S和P_k之间连边即可。

所谓距离s最近的点，实际上就是x_k+y_k最小的点。

图的构建方法

按照上一节介绍的方法，我们可以构建出一个至多含有8n条边的图。可是如何构造呢？如果对于每个点s，把所有的点都判断一次取最小值，那么复杂度是O(n²)，没有任何意义。下面我们考虑设计一个高效的算法，实现“找到每个点的R₁区域内，离其最近的点”的操作。

找s的R₁区域内离s最近的点，实际上就是找s的R₁区域内x+y最小的点。

我们把所有的点按照x从小到大排序：x₁≤x₂≤…≤x_n。

建立一个抽象数据结构T。T中的每个元素对应平面上的一个点(x,y)，该元素的第一关键字等于y-x，第二关键字等于y+x。

从P_n到P₁逐个处理每个点。处理Pk的时候，令P_k+1, P_k+2, …, P_n都已经存入到T中。某个点Q(x,y)如果落在P_k的R₁区间内，必须满足：

1.       x≥x_k

2.       y-x>y_k-x_k

要满足第一个条件，Q必须属于集合{P_k+1, P_k+2, …, P_n}，即Q必然在T中。

要满足第二个条件，Q在T中的第一关键字必须大于y_k-x_k(定值)。

因为我们要使得|P_kQ|最小，所以我们实际上就是：从T的第一关键字大于某常数的所有元素中，寻找第二关键字最小的元素。

很明显，T可以用平衡二叉树来实现。按照第一关键字有序来建立平衡树，对于平衡树每个节点都记录以其为根的子树中第二关键字最小的是哪个元素。查询、插入的时间复杂度都是O(logn)。

平衡二叉树也可以用线段树代替。

对于P_k，找到符合上述条件并使|P_kQ|最小的Q之后，在P_k和Q之间连一条边，并将P_k插入T；继续处理P_k-1(除非k=1)。

经过上面的处理，我们就把每个点在R₁区域内的最近点求出来了。同样的处理R₂, R₃, …, R₈即可把整个离散图构建出来。

一点优化

如果把R₁, R₂, …, R₈分别处理，则整个算法的复杂度系数过大。

我们很容易注意到，R₁和R₅是对称的，只要处理其中一个区域即可。根据对称性，我们只要处理R₁, R₂, R₃, R₄这四个区域。

如果点(x,y)在P_s的R₁区域内，则：

1.       x≥x_k

2.       y-x>y_k-x_k

如果点(x,y)在P_s的R₂区域内，则：

1.       x≥x_k

2.       y-x<y_k-x_k

以上两组条件仅是一个”>”和”<”的区别。

处理R₁的时候，任意时刻处理P_k，我们希望找T中第一关键字大于某常数的第二关键字最小元素；处理R₂的时候，任意时刻处理P_k，我们要找的就是T中第一关键字小于某常数的第二关键字最小元素。

因而很容易发现，R₁和R₂可以和在一起处理。

这样我们只要处理R₁+R₂、R₃+R₄这两种情况即可。时间复杂度的常系数从8降低到了2。

我们按照这样的方法建立的离散图至多含有8n条边。对该图求最小生成树的时间复杂度为O(nlogn)；之前建图的复杂度也是O(nlogn)，所以总时间复杂度O(nlogn)。空间复杂度O(n)。

总结

这个题目最值得称道的地方就是“分区域”。“分区域”充分利用了平面性质，结合一般情况下最小生成树都具有的环切性质，该方法取得了奇效。

我们研究问题的时候也应该注意充分利用已有信息。