题目描述：
一个规模为 W*H 的长方形 ， 其中 W*H＝40；
然后游戏依次随机生成10个块，这10个块为以下之一：
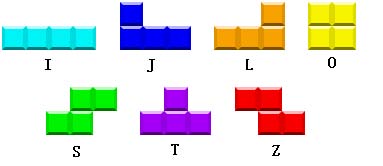
题目特别限制：不能使后面方块的某个格子在前面方块的下面。
求给定的这十个块能否拼成一个W*H的长方形。
题目分析：
首先规模不大，方块有10个，长方形面积为40，所以考虑深度优先搜索！
考虑到方块的旋转，比如 I 可以旋转变成 ---- ， 上述7种方块一共可以形成19种放置方式。
我们可以将这19种放置方式的位移向量用静态数组表示出来。
搜索顺序为依次从每一列选取未方格位置的最低点，在该位置放入给定方块，通过约束条件
进行剪枝，进入下一层深度搜索。
有一个比较简单的剪枝：若在放置方块P后，若在长方形中造成了空洞，则应该剪去。这很容
易判断，放置后，下方为空，则剪枝。
参考程序：
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<queue>
#define maxn 45
using namespace std ;
// state[i] 表示放置状态 I 的各种相对位移向量
// 里面的4组数据表示4个小块的位移
const int state[19][4][2] =
{
{{0,0},{0,1},{0,2},{0,3}}, //0
{{0,0},{1,0},{2,0},{3,0}}, //1
{{0,0},{0,1},{0,2},{1,0}}, //2
{{0,0},{1,0},{2,0},{2,1}}, //3
{{0,0},{0,1},{0,2},{-1,2}}, //4
{{0,0},{0,1},{1,1},{2,1}}, //5
{{0,0},{0,1},{0,2},{1,2}}, //6
{{0,0},{0,1},{1,0},{2,0}}, //7
{{0,0},{1,0},{1,1},{1,2}}, //8
{{0,0},{1,0},{2,0},{2,-1}}, //9
{{0,0},{0,1},{1,0},{1,1}}, //10
{{0,0},{0,1},{1,1},{1,2}}, //11
{{0,0},{0,1},{-1,1},{1,0}}, //12
{{0,0},{0,1},{0,2},{1,1}}, //13
{{0,0},{1,0},{2,0},{1,1}}, //14
{{0,0},{0,1},{0,2},{-1,1}}, //15
{{0,0},{0,1},{1,1},{-1,1}}, //16
{{0,0},{0,1},{-1,1},{-1,2}}, //17
{{0,0},{1,0},{1,1},{2,1}}, //18
} ;
const int idx[8] = {0,2,6,10,11,13,17,19}; // 索引数组
const char ch[] = "IJLOSTZ" ; // 字母映射成数字
int N , M , bd[maxn][maxn] , w[maxn];
inline bool IsOut(int x ,int y){ // 判断是否出界
return x<0||y<0||x>=M||y>=N ;
}
void put(int x,int y ,int u , int sig){ // 在(x,y)处放置方块u,标号sig
int i ,cx ,cy;
for(i = 0 ; i < 4 ; ++i ){
cx = x + state[u][i][0] ;
cy = y + state[u][i][1] ;
bd[cx][cy] = sig ;
}
}
bool check(int x,int y ,int u){ // 检查是否有空洞
int i , cx ,cy ;
for(i = 0 ; i<4 ; ++i){
cx = x + state[u][i][0] ;
cy = y + state[u][i][1] ;
if(!IsOut(cx-1,cy) && !bd[cx-1][cy]) return 0 ;
}
return 1 ;
}
bool DFS(int dep){
if(dep > 9) return 1 ;
int i , j , k , u ,t , cx , cy , chk;
for(j = 0 ; j < N ; ++j){
for(i = 0 ; i < M && bd[i][j] ; ++i) ; // 寻找j列中尚未放置的第一个格子
if(i == M) continue ;
for(k = idx[u=w[dep]] ; k < idx[u+1] ; ++k ){ // 对方块的各种旋转状态进行试探
chk = 0 ;
for(t=0 ; t<4 &&!chk; ++t ){
cx = i + state[k][t][0] ;
cy = j + state[k][t][1] ;
if((IsOut(cx,cy)||bd[cx][cy]) ) // 不满足约束
chk = 1 ;
}
if(chk == 1) continue ;
put(i,j,k,dep+1); // 放置
if(check(i,j,k) && DFS(dep+1)) return 1 ;
put(i,j,k,0); // 清理
}
}
return 0;
}
inline int findp(char chr){
int i ;
for(i = 0 ; i < 7 ; ++ i)
if(chr == ch[i]) return i ;
}
int main(){
int i , j;
char str[2] ;
while(scanf("%d%d",&N,&M)!=EOF && (N+M)){
for(i=0 ; i<10 ; ++i){
scanf("%s",str);
w[i] = findp(str[0]) ;
}
memset(bd , 0 ,sizeof(bd));
if( DFS(0) )
printf("Yes\n");
else
printf("No\n");
}
return 0 ;
}