
转自:
http://blog.chinaunix.net/u3/98913/showart_2004280.html我们通常把一些公用函数制作成函数库,供其它程序使用。函数库分为静态库和动态库两
种。静态库在程序编译时会被连接到目标代码中,程序运行时将不再需要该静态库。动态
库在程序编译时并不会被连接到目标代码中,而是在程序运行是才被载入,因此在程序运
行时还需要动态库存在。本文主要通过举例来说明在Linux中如何创建静态库和动态库,以
及使用它们。
在创建函数库前,我们先来准备举例用的源程序,并将函数库的源程序编译成.o文件。
第1步:编辑得到举例的程序--hello.h、hello.c和main.c;
hello.c(见程序2)是函数库的源程序,其中包含公用函数hello,该函数将在屏幕上输出"
Hello XXX!"。hello.h(见程序1)为该函数库的头文件。main.c(见程序3)为测试库文件的
主程序,在主程序中调用了公用函数hello。
#ifndef HELLO_H
#define HELLO_H
void hello(const char *name);
#endif //HELLO_H
程序1: hello.h
#include <stdio.h>
void hello(const char *name)
{
printf("Hello %s!\n", name);
}
程序2: hello.c
#include "hello.h"
int main()
{
hello("everyone");
return 0;
}
程序3: main.c
第2步:将hello.c编译成.o文件;
无论静态库,还是动态库,都是由.o文件创建的。因此,我们必须将源程序hello.c通过g
cc先编译成.o文件。
在系统提示符下键入以下命令得到hello.o文件。
# gcc -c hello.c
#
我们运行ls命令看看是否生存了hello.o文件。
# ls
hello.c hello.h hello.o main.c
#
在ls命令结果中,我们看到了hello.o文件,本步操作完成。
下面我们先来看看如何创建静态库,以及使用它。
第3步:由.o文件创建静态库;
静态库文件名的命名规范是以lib为前缀,紧接着跟静态库名,扩展名为.a。例如:我们将
创建的静态库名为myhello,则静态库文件名就是libmyhello.a。在创建和使用静态库时,
需要注意这点。创建静态库用ar命令。
在系统提示符下键入以下命令将创建静态库文件libmyhello.a。
# ar crv libmyhello.a hello.o
#
我们同样运行ls命令查看结果:
# ls
hello.c hello.h hello.o libmyhello.a main.c
#
ls命令结果中有libmyhello.a。
第4步:在程序中使用静态库;
静态库制作完了,如何使用它内部的函数呢?只需要在使用到这些公用函数的源程序中包
含这些公用函数的原型声明,然后在用gcc命令生成目标文件时指明静态库名,gcc将会从
静态库中将公用函数连接到目标文件中。注意,gcc会在静态库名前加上前缀lib,然后追
加扩展名.a得到的静态库文件名来查找静态库文件。
在程序3:main.c中,我们包含了静态库的头文件hello.h,然后在主程序main中直接调用公
用函数hello。下面先生成目标程序hello,然后运行hello程序看看结果如何。
(# gcc -o hello main.c -L. -lmyhello??)
#gcc main.c libmyhello.a -o main
# ./hello
Hello everyone!
#
我们删除静态库文件试试公用函数hello是否真的连接到目标文件 hello中了。
# rm libmyhello.a
rm: remove regular file `libmyhello.a'? y
# ./hello
Hello everyone!
#
程序照常运行,静态库中的公用函数已经连接到目标文件中了。
我们继续看看如何在Linux中创建动态库。我们还是从.o文件开始。
第5步:由.o文件创建动态库文件;
动态库文件名命名规范和静态库文件名命名规范类似,也是在动态库名增加前缀lib,但其
文件扩展名为.so。例如:我们将创建的动态库名为myhello,则动态库文件名就是libmyh
ello.so。用gcc来创建动态库。
在系统提示符下键入以下命令得到动态库文件libmyhello.so。
# gcc -shared -fPCI -o libmyhello.so hello.o
#
我们照样使用ls命令看看动态库文件是否生成。
# ls
hello.c hello.h hello.o libmyhello.so main.c
#
第6步:在程序中使用动态库;
在程序中使用动态库和使用静态库完全一样,也是在使用到这些公用函数的源程序中包含
这些公用函数的原型声明,然后在用gcc命令生成目标文件时指明动态库名进行编译。我们
先运行gcc命令生成目标文件,再运行它看看结果。
# gcc -o hello main.c -L. -lmyhello
# ./hello
./hello: error while loading shared libraries: libmyhello.so: cannot open shar
ed object file: No such file or directory
#
哦!出错了。快看看错误提示,原来是找不到动态库文件libmyhello.so。程序在运行时,
会在/usr/lib和/lib等目录中查找需要的动态库文件。若找到,则载入动态库,否则将提
示类似上述错误而终止程序运行。我们将文件libmyhello.so复制到目录/usr/lib中,再试
试。
# mv libmyhello.so /usr/lib
# ./hello
Hello everyone!
#
成功了。这也进一步说明了动态库在程序运行时是需要的。
我们回过头看看,发现使用静态库和使用动态库编译成目标程序使用的gcc命令完全一样,
那当静态库和动态库同名时,gcc命令会使用哪个库文件呢?抱着对问题必究到底的心情,
来试试看。
先删除除.c和.h外的所有文件,恢复成我们刚刚编辑完举例程序状态。
# rm -f hello hello.o /usr/lib/libmyhello.so
# ls
hello.c hello.h main.c
#
在来创建静态库文件libmyhello.a和动态库文件libmyhello.so。
# gcc -c hello.c
# ar cr libmyhello.a hello.o
# gcc -shared -fPCI -o libmyhello.so hello.o
# ls
hello.c hello.h hello.o libmyhello.a libmyhello.so main.c
#
通过上述最后一条ls命令,可以发现静态库文件libmyhello.a和动态库文件libmyhello.s
o都已经生成,并都在当前目录中。然后,我们运行gcc命令来使用函数库myhello生成目标
文件hello,并运行程序 hello。
# gcc -o hello main.c -L. -lmyhello
# ./hello
./hello: error while loading shared libraries: libmyhello.so: cannot open shar
ed object file: No such file or directory
#
从程序hello运行的结果中很容易知道,当静态库和动态库同名时, gcc命令将优先使用动
态库。
Note:
编译参数解析
最主要的是GCC命令行的一个选项:
-shared 该选项指定生成动态连接库(让连接器生成T类型的导出符号表,有时候也生成弱连接W类型的导出符号),不用该标志外部程序无法连接。相当于一个可执行文件
l -fPIC:表示编译为位置独立的代码,不用此选项的话编译后的代码是位置相关的所以动态载入时是通过代码拷贝的方式来满足不同进程的需要,而不能达到真正代码段共享的目的。
l -L.:表示要连接的库在当前目录中
l -ltest:编译器查找动态连接库时有隐含的命名规则,即在给出的名字前面加上lib,后面加上.so来确定库的名称
l LD_LIBRARY_PATH:这个环境变量指示动态连接器可以装载动态库的路径。
l 当然如果有root权限的话,可以修改/etc/ld.so.conf文件,然后调用 /sbin/ldconfig来达到同样的目的,不过如果没有root权限,那么只能采用输出LD_LIBRARY_PATH的方法了。
调用动态库的时候有几个问题会经常碰到,有时,明明已经将库的头文件所在目录 通过 “-I” include进来了,库所在文件通过 “-L”参数引导,并指定了“-l”的库名,但通过ldd命令察看时,就是死活找不到你指定链接的so文件,这时你要作的就是通过修改 LD_LIBRARY_PATH或者/etc/ld.so.conf文件来指定动态库的目录。通常这样做就可以解决库无法链接的问题了。
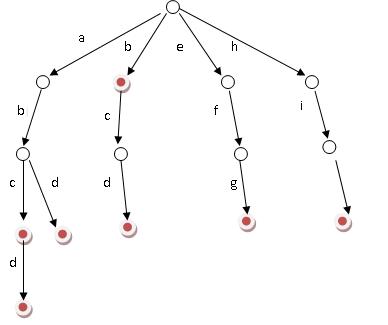
Trie,又称字典树、单词查找树,是一种树形结构,用于保存大量的字符串。它的优点是:利用字符串的公共前缀来节约存储空间。
相对来说,Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.当然,或许用左儿子右兄弟的方法建树的话,可能会好点.
其基本性质可以归纳为:
1. 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
其基本操作有:查找 插入和删除,当然删除操作比较少见.我在这里只是实现了对整个树的删除操作,至于单个word的删除操作也很简单.
搜索字典项目的方法为:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
(3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
其他操作类似处理.
1
 /**//*
/**//*
2 Name: Trie树的基本实现
Name: Trie树的基本实现
3 Author: MaiK
Author: MaiK
4 Description: Trie树的基本实现 ,包括查找 插入和删除操作*/
Description: Trie树的基本实现 ,包括查找 插入和删除操作*/
5 #include<algorithm>
#include<algorithm>
6 #include<iostream>
#include<iostream>
7 using namespace std;
using namespace std;
8
9 const int sonnum=26,base='a';
const int sonnum=26,base='a';
10 struct Trie
struct Trie
11

 {
{
12 int num;//to remember how many word can reach here,that is to say,prefix
int num;//to remember how many word can reach here,that is to say,prefix
13 bool terminal;//If terminal==true ,the current point has no following point
bool terminal;//If terminal==true ,the current point has no following point
14 struct Trie *son[sonnum];//the following point
struct Trie *son[sonnum];//the following point
15 };
};
16 Trie *NewTrie()// create a new node
Trie *NewTrie()// create a new node
17

 {
{
18 Trie *temp=new Trie;
Trie *temp=new Trie;
19 temp->num=1;temp->terminal=false;
temp->num=1;temp->terminal=false;
20 for(int i=0;i<sonnum;++i)temp->son[i]=NULL;
for(int i=0;i<sonnum;++i)temp->son[i]=NULL;
21 return temp;
return temp;
22 }
}
23 void Insert(Trie *pnt,char *s,int len)// insert a new word to Trie tree
void Insert(Trie *pnt,char *s,int len)// insert a new word to Trie tree
24

 {
{
25 Trie *temp=pnt;
Trie *temp=pnt;
26 for(int i=0;i<len;++i)
for(int i=0;i<len;++i)
27

 {
{
28 if(temp->son[s[i]-base]==NULL)temp->son[s[i]-base]=NewTrie();
if(temp->son[s[i]-base]==NULL)temp->son[s[i]-base]=NewTrie();
29 else temp->son[s[i]-base]->num++;
else temp->son[s[i]-base]->num++;
30 temp=temp->son[s[i]-base];
temp=temp->son[s[i]-base];
31 }
}
32 temp->terminal=true;
temp->terminal=true;
33 }
}
34 void Delete(Trie *pnt)// delete the whole tree
void Delete(Trie *pnt)// delete the whole tree
35

 {
{
36 if(pnt!=NULL)
if(pnt!=NULL)
37

 {
{
38 for(int i=0;i<sonnum;++i)if(pnt->son[i]!=NULL)Delete(pnt->son[i]);
for(int i=0;i<sonnum;++i)if(pnt->son[i]!=NULL)Delete(pnt->son[i]);
39 delete pnt;
delete pnt;
40 pnt=NULL;
pnt=NULL;
41 }
}
42 }
}
43 Trie* Find(Trie *pnt,char *s,int len)//trie to find the current word
Trie* Find(Trie *pnt,char *s,int len)//trie to find the current word
44

 {
{
45 Trie *temp=pnt;
Trie *temp=pnt;
46 for(int i=0;i<len;++i)
for(int i=0;i<len;++i)
47 if(temp->son[s[i]-base]!=NULL)temp=temp->son[s[i]-base];
if(temp->son[s[i]-base]!=NULL)temp=temp->son[s[i]-base];
48 else return NULL;
else return NULL;
49 return temp;
return temp;
50 }
}
今天,终于达到150题啦(*^__^*) 嘻嘻……继续加油

问题:
http://poj.org/problem?id=1016思路:
纯模拟,需要细心...
代码:
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h>
4 #define NUM 10 /* 0..9 */
5 #define UP 15
6 #define INPUT_LEN 81
7 #define MAX_LEN 31
8 char input[INPUT_LEN], inv[UP][MAX_LEN];
9 int count[NUM];
10
11 void
12 generate(char *src, char *dst)
13 {
14 int i, index, len = strlen(src);
15 memset(count, 0, sizeof(count));
16 for(i=0; i<len; i++)
17 ++count[src[i]-'0'];
18
19 index = 0;
20 for(i=0; i<NUM; i++) {
21 if(count[i] > 0) {
22 if(count[i] >= 10) {
23 dst[index++] = (count[i]/10)+'0';
24 dst[index++] = (count[i]%10)+'0';
25 } else {
26 dst[index++] = count[i]+'0';
27 }
28 dst[index++] = i+'0';
29 }
30 }
31 }
32
33 void
34 solve()
35 {
36 int i, index = 0;
37 generate(input, inv[index]);
38 if(strcmp(input, inv[index]) == 0) {
39 printf("%s is self-inventorying\n", input);
40 return;
41 }
42 ++index;
43 while(index < UP) {
44 generate(inv[index-1], inv[index]);
45 if(strcmp(inv[index], inv[index-1]) == 0) {
46 printf("%s is self-inventorying after %d steps\n", input, index);
47 return;
48 }
49 for(i=index-2; i>=0; i--)
50 if(strcmp(inv[index], inv[i]) == 0) {
51 printf("%s enters an inventory loop of length %d\n", input, index-i);
52 return;
53 }
54 if(index >= 1)
55 if(strcmp(inv[index], input) == 0) {
56 printf("%s enters an inventory loop of length %d\n", input, index+1);
57 return;
58 }
59 ++index;
60 }
61 printf("%s can not be classified after 15 iterations\n", input);
62 }
63
64 int
65 main(int argc, char **argv)
66 {
67 while(scanf("%s", input) != EOF) {
68 if(strcmp(input, "-1") == 0)
69 break;
70 memset(inv, 0, sizeof(inv));
71 solve();
72 }
73 }
问题:
http://poj.org/problem?id=2418思路:
题意清晰明了,不难,用三种方法分别实现:
快速排序
动态生成节点的二叉查找树
静态分配节点的二叉查找树
结果发现,原来对于快速排序与静态分配节点都不是很熟悉,二维数组的快速排序分析见
http://www.cppblog.com/Joe/archive/2010/10/29/131746.html,而动态生成节点则需要注意如果函数需要修改指针,那么必须传递指向指针的指针,因为C是值传递的
另外,我以为静态分配节点应该比动态分配节点节约很多时间的,结果居然差不多...而快速排序在这题明显是最耗时的
代码(快排)
1 /* 35640K 1844MS */
2 #include<stdio.h>
3 #include<stdlib.h>
4 #include<string.h>
5 #define MAX_LEN 36
6 #define MAX_NUM 1000001
7 char species[MAX_NUM][MAX_LEN];
8
9 int
10 cmp(const void *arg1, const void *arg2)
11 {
12 return strcmp((char *)arg1, (char *)arg2);
13 }
14
15 int
16 main(int argc, char **argv)
17 {
18 int i, count, total = 0;
19 while(gets(species[total]) != NULL)
20 ++total;
21 qsort(species, total, sizeof(species[0]), cmp);
22 count = 1;
23 for(i=1; i<total; i++) {
24 if(strcmp(species[i], species[i-1]) == 0)
25 ++count;
26 else {
27 printf("%s %.4f\n", species[i-1], (count*100.0)/total);
28 count = 1;
29 }
30 }
31 printf("%s %.4f\n", species[total-1], (count*100.0)/total);
32 }
代码(动态分配节点的BST,原本想实现下destroy函数的,结果怕麻烦就留给系统回收吧(*^__^*) 嘻嘻……)
1 /* binary search tree(dynamic allocation) */
2 /* 544K 1188MS */
3 #include<stdio.h>
4 #include<stdlib.h>
5 #include<string.h>
6 #include<assert.h>
7 #define MAX_LEN 36
8 struct Node {
9 char spec[MAX_LEN];
10 int count;
11 struct Node *left, *right;
12 };
13 int total;
14
15 struct Node *
16 create_node(char *str)
17 {
18 struct Node *node = (struct Node *)malloc(sizeof(struct Node));
19 assert(node != NULL);
20 strcpy(node->spec, str);
21 node->left = node->right = NULL;
22 node->count = 1;
23 return node;
24 }
25
26 void
27 insert(struct Node **root, char *str)
28 {
29 int ret;
30 struct Node *node;
31 if(*root==NULL) {
32 *root = create_node(str);
33 return;
34 }
35 ret = strcmp((*root)->spec, str);
36 if(ret == 0)
37 ++((*root)->count);
38 else if(ret < 0)
39 insert(&((*root)->right), str);
40 else
41 insert(&((*root)->left), str);
42 }
43
44 void
45 inorder(struct Node *root)
46 {
47 if(root == NULL)
48 return;
49 inorder(root->left);
50 printf("%s %.4f\n", root->spec, (root->count)*100.0/total);
51 inorder(root->right);
52 }
53
54 void
55 destroy(struct Node **root)
56 {
57 }
58
59 int
60 main(int argc, char **argv)
61 {
62 char str[MAX_LEN];
63 struct Node *bst = NULL;
64 total = 0;
65 while(gets(str) != NULL) {
66 ++total;
67 insert(&bst, str);
68 }
69 inorder(bst);
70 }
代码(静态分配节点的BST)
1 /* binary search tree(static allocation) */
2 /* 492K 1188MS */
3 #include<stdio.h>
4 #include<stdlib.h>
5 #include<string.h>
6 #include<assert.h>
7 #define MAX_LEN 36
8 #define MAX_NUM 10007
9 #define ROOT 1
10 struct Node {
11 char spec[MAX_LEN];
12 int count;
13 int left, right;
14 }bst[MAX_NUM];
15 int cur_index, total;
16
17 int
18 find(int root, char *str)
19 {
20 int ret, parent, cur = root;
21 while(cur != 0) {
22 parent = cur;
23 ret = strcmp(bst[cur].spec, str);
24 if(ret == 0) {
25 ++bst[cur].count;
26 return 0;
27 } else if(ret < 0) {
28 cur = bst[cur].right;
29 } else {
30 cur = bst[cur].left;
31 }
32 }
33 return parent;
34 }
35
36 #define ADD(index, str) { \
37 strcpy(bst[index].spec, str); \
38 bst[index].left = bst[index].right = 0; \
39 bst[index].count = 1; \
40 ++index; }
41
42 void
43 insert(int parent, char *str)
44 {
45 int ret = strcmp(bst[parent].spec, str);
46 assert(ret != 0);
47 if(ret < 0)
48 bst[parent].right = cur_index;
49 else
50 bst[parent].left = cur_index;
51 ADD(cur_index, str);
52 }
53
54 void
55 inorder(int index)
56 {
57 if(index == 0)
58 return;
59 inorder(bst[index].left);
60 printf("%s %.4f\n", bst[index].spec, (bst[index].count*100.0)/total);
61 inorder(bst[index].right);
62 }
63
64 int
65 main(int argc, char **argv)
66 {
67 int parent;
68 char str[MAX_LEN];
69 total = 1;
70 cur_index = ROOT;
71 gets(str);
72 ADD(cur_index, str); /* create the root node first */
73 while(gets(str) != NULL) {
74 ++total;
75 if((parent=find(ROOT, str)) > 0)
76 insert(parent, str);
77 }
78 inorder(ROOT);
79 }
在将qsort函数应用于对指针数组与二维数组排序时,传递给compare函数的参数类型是不同的首先,我们举个简单的例子,先将qsort对整数数组排序:
1 int
2 cmp(const void *arg1, const void *arg2)
3 {
4 return (*(int *)arg1)-(*(int *)arg2);
5 }
6
7 int
8 main(int argc, char **argv)
9 {
10 int i;
11 int arr[] = {3, 1, 5, 2, 4};
12 qsort(arr, sizeof(arr)/sizeof(arr[0]), sizeof(int), cmp);
13 }
排序针对的是数组里的元素而言的,这里整数数组的元素就是整数,因此qsort的第三个参数就是sizeof(int),而传递给比较函数cmp的参数就是相对应的指向整数的指针
接着,我们来看看指针数组的情形:
1 int
2 cmp(const void *arg1, const void *arg2)
3 {
4 return strcmp((*(char **)arg1), (*(char **)arg2));
5 }
6
7 int
8 main(int argc, char **argv)
9 {
10 int i;
11 /* pointer array */
12 char *str[] = {"java", "c", "python", "perl"};
13 qsort(str, sizeof(str)/sizeof(str[0]), sizeof(char *), cmp);
14 }
这里的理解其实跟整数数组差不多,关键是抓住数组里元素的类型,既然称之为指针数组,那数组元素的类型自然就是指针,因此qsort的第三个参数就是sizeof(char *),而传递给比较函数cmp的参数就是相对应的指向指针的指针,这里即char **类型
二维数组的理解最为复杂,代码如下:
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h>
4
5 int
6 cmp1(const void *arg1, const void *arg2)
7 {
8 return strcmp((*((char (*)[])arg1)), (*((char (*)[])arg2)));
9 }
10
11 int
12 cmp2(const void *arg1, const void *arg2)
13 {
14 return strcmp((char *)arg1, (char *)arg2);
15 }
16
17 int
18 main(int argc, char **argv)
19 {
20 int i;
21 char str1[4][8] = {"java", "c", "python", "peal"};
22 printf("COMPARE-FUNCTION-1\n");
23 qsort(str1, 4, sizeof(str1[0]), cmp1);
26
27 char str2[4][8] = {"java", "c", "python", "peal"};
28 printf("COMPARE-FUNCTION-2\n");
29 qsort(str2, 4, sizeof(str2[0]), cmp2);
34 }
这里cmp1与cmp2都能正常的工作(*^__^*) 嘻嘻……
还是按照上述方法来分析,抓住数组元素的类型来入手,二维数组实际上就是数组的数组,因此二维数组的元素类型就是一维数组,因此qsort的第三个参数就是sizeof(str1[0])或sizeof(str2[0]),那传递给比较函数的参数应该就是指向数组的指针,这点可以通过gdb设置断点来得到证实:
1 (gdb) p &str1[0]
2 $1 = (char (*)[8]) 0xbffff2cc
3 (gdb) p &str1[1]
4 $2 = (char (*)[8]) 0xbffff2d4
5
6 Breakpoint 2, cmp1 (arg1=0xbffff2cc, arg2=0xbffff2d4) at char_test2.c:8
7 8 return strcmp((*((char (*)[])arg1)), (*((char (*)[])arg2)));
8 (gdb) p arg1
9 $3 = (const void *) 0xbffff2cc
10 (gdb) p arg2
11 $4 = (const void *) 0xbffff2d4
12 (gdb) p *(char (*)[])arg1
13 $5 = "j"
14 (gdb) p *(char (*)[8])arg1
15 $6 = "java\000\000\000"
通过第2行与第9行的比较可以发现,比较函数的参数arg1其实就是&str1[0],类型为char (*)[],这也是为什么cmp1能正常工作的原因
那么cmp2呢,它为什么正确呢?
在cmp1中:
strcmp((*((char (*)[])arg1)), (*((char (*)[])arg2))); 这里传递给strcmp的参数之所以不会出错,是因为我们将arg1解地址操作获得一个数组,而数组名其实是指向数组首元素的指针,arg1既然是指向str1[0]这个一维数组的指针,而str1[0]本身其实就是指向这个一维数组的指针,也就是说arg1其实就是str1[0],因此cmp2能够正常工作
1 (gdb) p &str1[0]
2 $3 = (char (*)[8]) 0xbffff2cc
3 (gdb) p &str1[0][0]
4 $4 = 0xbffff2cc "java"
5 (gdb) p arg1
6 $5 = (const void *) 0xbffff2cc
7 (gdb) p (char *)arg1
8 $6 = 0xbffff2cc "java"
额...貌似越说越复杂的样子,不过这是我理解的过程,见谅...
问题:
http://poj.org/problem?id=1657思路:
原本以为是搜索题,结果发现居然都可以推导出来(*^__^*) 嘻嘻……0MS
睡觉前AC个题,感觉蛮好
代码(写的比较繁琐):
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h>
4 #define Diff(a, b) ((a)>(b) ? ((a)-(b)) : ((b)-(a)))
5 #define Max(a, b) ((a)>(b) ? (a) : (b))
6 #define MAX_LEN 3
7 typedef enum {
8 Black,
9 White
10 }Color;
11
12 int
13 is_linear(char *src, char *dst)
14 {
15 if(src[0]==dst[0] || src[1]==dst[1])
16 return 1;
17 return 0;
18 }
19
20 int
21 is_oblique(char *src, char *dst)
22 {
23 int x_diff = Diff(src[0], dst[0]);
24 int y_diff = Diff(src[1], dst[1]);
25 if(x_diff == y_diff)
26 return 1;
27 return 0;
28 }
29
30 Color
31 black_or_white(char *src)
32 {
33 int x = src[0] - 'a' + 1;
34 int y = src[1] - '0';
35 if(x%2 == y%2)
36 return White;
37 return Black;
38 }
39
40 void
41 solve(char *src, char *dst)
42 {
43 int a, b, c, d, x_diff, y_diff;
44 x_diff = Diff(src[0], dst[0]);
45 y_diff = Diff(src[1], dst[1]);
46 a = Max(x_diff, y_diff); /* king */
47 if(is_linear(src, dst) || is_oblique(src, dst)) /* queen */
48 b = 1;
49 else
50 b = 2;
51
52 if(is_linear(src, dst)) /* rook */
53 c = 1;
54 else
55 c = 2;
56
57 if(is_oblique(src, dst)) /* bishop */
58 d = 1;
59 else if(black_or_white(src) != black_or_white(dst))
60 d = -1;
61 else
62 d = 2;
63
64 printf("%d %d %d ", a, b, c);
65 if(d == -1)
66 printf("Inf\n");
67 else
68 printf("%d\n", d);
69 }
70
71 int
72 main(int argc, char **argv)
73 {
74 int tests;
75 char begin[MAX_LEN], end[MAX_LEN];
76 scanf("%d", &tests);
77 while(tests--) {
78 scanf("%s %s", begin, end);
79 if(begin[0]==end[0] && begin[1]==end[1])
80 printf("0 0 0 0\n");
81 else
82 solve(begin, end);
83 }
84 }
问题:
http://poj.org/problem?id=3400思路:
这题就是个悲剧...
应该算是简单的深搜题,结果花了我一个上午
画了好几颗递归调用树也不知道为什么会出错...抓狂...
最后发现,一直出错的原因是在写代码的时候将递归函数的参数直接修改,导致后续的“同一层”的回溯调用出错,啊啊啊...
代码:
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h>
4 #define MAX_LEN 11
5 struct Stone {
6 int weight;
7 int cost;
8 }stones[MAX_LEN];
9 int N, D;
10 int total_cost, max_cost, hash[MAX_LEN];
11
12 void
13 dfs(char bunker, int weight_a, int cost_a, int weight_b, int cost_b)
14 {
15 int i, w, c, mark = 0;
16 if(total_cost-cost_a<=max_cost)
17 return;
18 for(i=0; i<N; i++) {
19 if(!hash[i]) {
20 mark = 1;
21 hash[i] = 1;
22 switch(bunker) {
23 case 'A':
24 w = weight_a+stones[i].weight;
25 c = cost_a+stones[i].cost;
26 if(w-weight_b <= D)
27 dfs('A', w, c, weight_b, cost_b);
28 else
29 dfs('B', w, c, weight_b, cost_b);
30 break;
31 case 'B':
32 w = weight_b+stones[i].weight;
33 c = cost_b+stones[i].cost;
34 if(w-weight_a <= D)
35 dfs('B', weight_a, cost_a, w, c);
36 else
37 dfs('A', weight_a, cost_a, w, c);
38 break;
39 }
40 hash[i] = 0;
41 }
42 }
43 if(!mark)
44 max_cost = max_cost<cost_b ? cost_b : max_cost;
45 }
46
47 int
48 main(int argc, char **argv)
49 {
50 int i;
51 while(scanf("%d %d", &N, &D) != EOF) {
52 total_cost = 0;
53 for(i=0; i<N; i++) {
54 scanf("%d %d", &stones[i].weight, &stones[i].cost);
55 total_cost += stones[i].cost;
56 }
57 max_cost = 0;
58 memset(hash, 0, sizeof(hash));
59 dfs('A', 0, 0, 0, 0);
60 printf("%d\n", max_cost);
61 }
62 }
在图书馆偶见《系统程序员成长计划》,作者是李先静
记得之前曾经见过作者的博客,可惜没能仔细查看
如今,赶紧借了回来,刚看了前几章,觉得写的很好,也颇有收获(其实,Linux+Vim+C特别符合咱胃口(*^__^*) 嘻嘻……)
书中描述C语言的特点:简单、高效、直观,实在是言简意赅
说实话,我最喜欢的就是C语言
Keep Fighting...
问题:
http://poj.org/problem?id=2312思路:
在
http://www.cppblog.com/Joe/archive/2010/10/23/130973.html中,参考网上代码采用了一种"新"的BFS方法来解题,该方法的一个缺点在于每个点可能多次进入队列,这也直接导致了单个点的多次扩展
其实,这题可以采用原始的BFS方法来做,只是不能再用普通的队列,而需要使用优先级队列
通过这题,使我对于宽度优先搜索有了新的认识
普通的BFS之所以能够找到最小的步数,关键在于它是单步扩展的,也就是说它首先罗列出所有在一步之内可以到达的点,然后再罗列所有在两步之内可以到达的点,类似于"1-1-1...-2-2-2...-3-3-3..."的方式
这题在扩展的时候并非都是一步,所以普通的BFS并不能找出正确的解,例如:
Y B
E T
假如我们以右、下、左、上的顺序进行扩展,那么我们将得出结果是3,而事实上只需要2
优先级队列之所以能够找出正确解,是因为它保证我们始终从最小步数的点开始扩展
代码(C++)
1 /* 0MS */
2 #include<iostream>
3 #include<cstdio>
4 #include<cstring>
5 #include<queue> /* priority queue */
6 using namespace std;
7
8 #define MAX_LEN 301
9 #define is_valid(x, y) ((x)>=0 && (x)<M && (y)>=0 && (y)<N)
10 char map[MAX_LEN][MAX_LEN];
11 const int dx[] = {0, 0, -1, 1};
12 const int dy[] = {-1, 1, 0, 0};
13 int M, N;
14 int you_x, you_y, target_x, target_y;
15 int visited[MAX_LEN][MAX_LEN];
16 struct Node {
17 int x, y;
18 int steps;
19 bool operator<(const Node &item) const {
20 return steps > item.steps;
21 }
22 }cur, next;
23 priority_queue<Node> states;
24
25 int
26 bfs()
27 {
28 int i;
29 memset(visited, 0, sizeof(visited));
30 while(!states.empty()) /* empty the queue */
31 states.pop();
32 next.x = you_x;
33 next.y = you_y;
34 next.steps = 0;
35 visited[you_x][you_y] = 1;
36 states.push(next);
37 while(!states.empty()) {
38 cur = states.top();
39 states.pop();
40 if(cur.x==target_x && cur.y==target_y)
41 return cur.steps;
42 for(i=0; i<4; i++) {
43 next.x = cur.x + dx[i];
44 next.y = cur.y + dy[i];
45 if(!visited[next.x][next.y]) {
46 visited[next.x][next.y] = 1;
47 if(map[next.x][next.y]=='E' || map[next.x][next.y]=='T') {
48 next.steps = cur.steps+1;
49 states.push(next);
50 } else if(map[next.x][next.y]=='B') {
51 next.steps = cur.steps+2;
52 states.push(next);
53 }
54 }
55 }
56 }
57 return -1;
58 }
59
60 int
61 main(int argc, char **argv)
62 {
63 int i, j;
64 while(scanf("%d %d", &M, &N)!=EOF && M && N) {
65 for(i=0; i<M; i++) {
66 scanf("%s", map[i]);
67 for(j=0; j<N; j++) {
68 if(map[i][j] == 'Y') {
69 you_x = i;
70 you_y = j;
71 } else if(map[i][j] == 'T') {
72 target_x = i;
73 target_y = j;
74 }
75 }
76 }
77 printf("%d\n", bfs());
78 }
79 }