B+ tree
From Wikipedia, the free encyclopedia
A simple B+ tree example linking the keys 1–7 to data values d
1-d
7. The linked list (red) allows rapid in-order traversal.
In computer science, a B+ tree or B plus tree is a type of tree
which represents sorted data in a way that allows for efficient
insertion, retrieval and removal of records, each of which is identified
by a key. It is a dynamic, multilevel index, with maximum and
minimum bounds on the number of keys in each index segment (usually
called a "block" or "node"). In a B+ tree, in contrast to a B-tree, all records are stored at the leaf level of the tree; only keys are stored in interior nodes.
The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context—in particular, filesystems. This is primarily because unlike binary search trees,
B+ trees have very high fanout (typically on the order of 100 or more),
which reduces the number of I/O operations required to find an element
in the tree.
NTFS, ReiserFS, NSS, XFS, and JFS filesystems all use this type of tree for metadata indexing. Relational database management systems such as IBM DB2[1], Informix[1], Microsoft SQL Server[1], Oracle 8[1], Sybase ASE[1], PostgreSQL[2], Firebird, MySQL[3] and SQLite[4] support this type of tree for table indices. Key-value database management systems such as CouchDB[5], Tokyo Cabinet[6] and Tokyo Tyrant support this type of tree for data access. InfinityDB[7] is a concurrent BTree.
[edit] Details
The order, or branching factor b of a B+ tree measures the
capacity of nodes (i.e. the number of children nodes) for internal nodes
in the tree. The actual number of children for a node, referred to here
as m, is constrained for internal nodes so that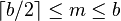 
. The root is an exception: it is allowed to have as few as two children. For example, if the order of a B+ tree is 7, each internal node
(except for the root) may have between 4 and 7 children; the root may
have between 2 and 7. Leaf nodes have no children , but are constrained
so that the number of keys must be at least 
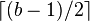and at most b − 1.
In the situation where a B+ tree is nearly empty, it only contains one
node, which is a leaf node. (The root is also the single leaf, in this
case.) This node is permitted to have as little as one key if necessary.
[edit] Search
The algorithm to perform a search for a record r follows pointers to
the correct child of each node until a leaf is reached. Then, the leaf
is scanned until the correct record is found (or until failure).
function search(record r)
u := root
while (u is not a leaf) do
choose the correct pointer in the node
move to the first node following the pointer
u := current node
scan u for r
This pseudocode assumes that no repetition is allowed.
[edit] Insertion
Perform a search to determine what bucket the new record should go in.
- if the bucket is not full, add the record.
- otherwise, split the bucket.
- allocate new leaf and move half the bucket's elements to the new bucket
- insert the new leaf's smallest key and address into the parent.
- if the parent is full, split it also
- add the middle key to the parent node
- repeat until a parent is found that need not split
- if the root splits, create a new root which has one key and two pointers.
[edit] Characteristics
For a b-order B+ tree with h levels of index:
- The maximum number of records stored is nmax = bh − bh − 1
- The minimum number of keys is
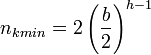
- The space required to store the tree is O(n)
- Inserting a record requires O(logbn) operations in the worst case
- Finding a record requires O(logbn) operations in the worst case
- Removing a (previously located) record requires O(logbn) operations in the worst case
- Performing a range query with k elements occurring within the range requires O(logbn + k) operations in the worst case.
[edit] Implementation
The leaves (the bottom-most index blocks) of the B+ tree are often linked to one another in a linked list; this makes range queries
or an (ordered) iteration through the blocks simpler and more efficient
(though the aforementioned upper bound can be achieved even without
this addition). This does not substantially increase space consumption
or maintenance on the tree. This illustrates one of the significant
advantages of a B+-tree over a B-tree;
in a B-tree, since not all keys are present in the leaves, such an
ordered linked list cannot be constructed. A B+-tree is thus
particularly useful as a database system index, where the data typically
resides on disk, as it allows the B+-tree to actually provide an
efficient structure for housing the data itself (this is described in [8] as index structure "Alternative 1").
If a storage system has a block size of B bytes, and the keys to be stored have a size of k, arguably the most efficient B+ tree is one where b = (B / k) − 1.
Although theoretically the one-off is unnecessary, in practice there is
often a little extra space taken up by the index blocks (for example,
the linked list references in the leaf blocks). Having an index block
which is slightly larger than the storage system's actual block
represents a significant performance decrease; therefore erring on the
side of caution is preferable.
If nodes of the B+ tree are organized as arrays of elements, then it
may take a considerable time to insert or delete an element as half of
the array will need to be shifted on average. To overcome this problem,
elements inside a node can be organized in a binary tree or a B+ tree
instead of an array.
B+ trees can also be used for data stored in RAM. In this case a
reasonable choice for block size would be the size of processor's cache line.
However, some studies have proved that a block size a few times larger
than the processor's cache line can deliver better performance if cache prefetching is used.
Space efficiency of B+ trees can be improved by using some compression techniques. One possibility is to use delta encoding
to compress keys stored into each block. For internal blocks, space
saving can be achieved by either compressing keys or pointers. For
string keys, space can be saved by using the following technique:
Normally the ith entry of an internal block contains the first
key of block i+1. Instead of storing the full key, we could store the
shortest prefix of the first key of block i+1 that is strictly greater
(in lexicographic order) than last key of block i. There is also a
simple way to compress pointers: if we suppose that some consecutive
blocks i, i+1...i+k are stored contiguously, then it will suffice to
store only a pointer to the first block and the count of consecutive
blocks.
All the above compression techniques have some drawbacks. First, a
full block must be decompressed to extract a single element. One
technique to overcome this problem is to divide each block into
sub-blocks and compress them separately. In this case searching or
inserting an element will only need to decompress or compress a
sub-block instead of a full block. Another drawback of compression
techniques is that the number of stored elements may vary considerably
from a block to another depending on how well the elements are
compressed inside each block.
[edit] History
The B tree was first described in the paper Organization and Maintenance of Large Ordered Indices. Acta Informatica 1: 173–189 (1972) by Rudolf Bayer
and Edward M. McCreight. There is no single paper introducing the B+
tree concept. Instead, the notion of maintaining all data in leaf nodes
is repeatedly brought up as an interesting variant. An early survey of B
trees also covering B+ trees is Douglas Comer: "The Ubiquitous B-Tree",
ACM Computing Surveys 11(2): 121–137 (1979). Comer notes that the B+
tree was used in IBM's VSAM data access software and he refers to an IBM
published article from 1973.
[edit] See also
[edit] References
[edit] External links