Posted on 2010-06-23 00:15
王之昊 阅读(514)
评论(0) 编辑 收藏 引用 所属分类:
初中风格的平面几何 、
二分 、
圆

题意:有四个圆大小不一,可以随意移动他们,求包围这四个圆的最小园?
首先应该是二分答案,变成一个判定性问题。
对于某个固定半径 R 的目标圆,假设它的圆心 C0 在(0,0)。其他四个圆的圆心 Pi 只要满足 | Pi - C0 | + ri <= R 即可。可以想象Pi 应当尽量的离 C0越远越好, 越远越有希望放下,当然在满足上面的条件下。
这样四个圆的圆心离原点的距离就确定了,现在可以想像成有
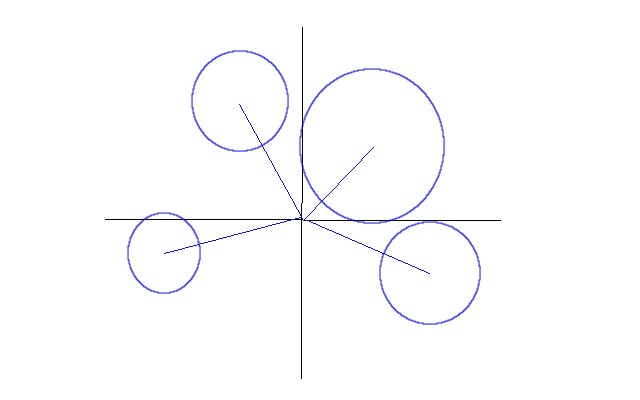
四个杠杆,每个杠杆的头上有一个圆,杠杆可以绕着原点转动,圆是刚性的,接着就判断这种情况是否可能发生.
实际上只要让他们一个挨着一个放就可以了.比如可以 放置第i个时,尽量挨着逆时针方向的前i-1个,并且判断会不会沿顺时针方向和前i-1个冲突.
这里还有些不太清楚的地方:比如顺序是否有关?