导读:http://www.cnblogs.com/zhjp11/archive/2010/02/26/1674227.html
现在要选择第k小的数字,一种比较简单的方法就是先排序,然后根据下标找出第k小的数字,这个时间复杂度为O(nlogn)
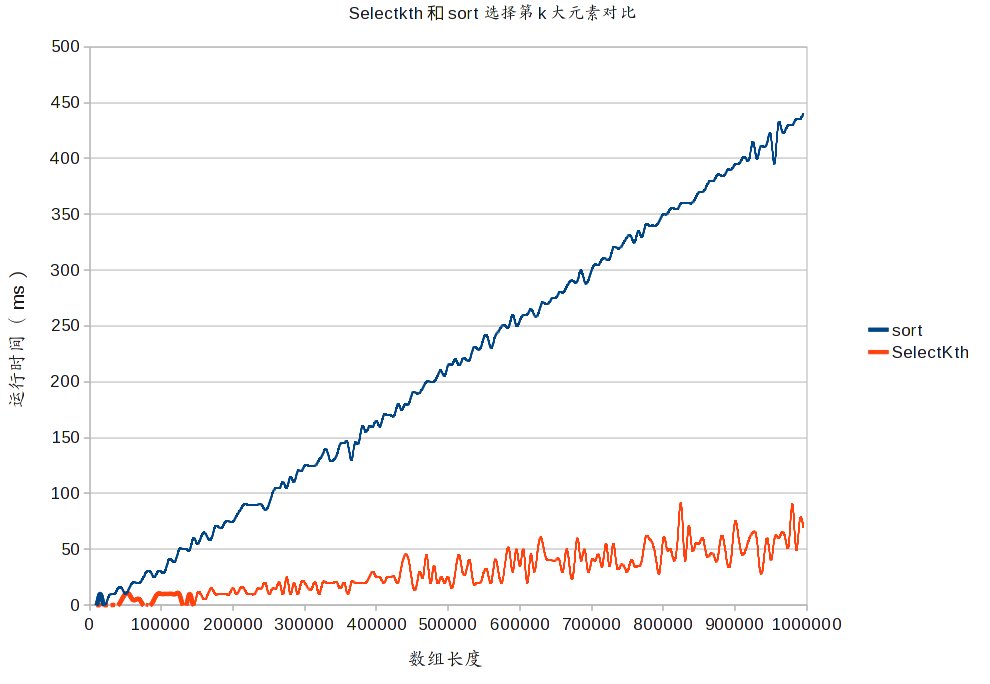
selectKth有点类似于快速排序,不过他的时间复杂度为O(n)。(就是导读中的解法3)
下面是一个运行时间的对比图,selectKth的运行时间有很明显的优势。
main.cpp
|
#include <iostream>
#include <cstdlib>
#include <algorithm>
#include "Record.h"
#include "Rand.h"
#include "SelectKth.h"
using namespace std;
const int MaxSize=1000000;
const int Step=5000;
int main()
{
Record record;
int A[MaxSize],B[MaxSize],C[MaxSize];
int curLen,i,kth;
for(curLen=Step;curLen<MaxSize;curLen+=Step)
{
for(i=0;i<curLen;i++)
{
A[i]=RandIn(0,1234567);
B[i]=A[i];
C[i]=A[i];
}
kth=RandIn(0,curLen)+1;
cout<<curLen<<"\t";
//sort
record.StartRecord();
sort(B,B+curLen);
cout<<B[kth-1]<<"\t";
record.PrintCostTime();
//select kth
record.StartRecord();
cout<<"\t"<<SelectKth(C,0,curLen-1,kth)<<"\t";
record.PrintCostTime();
cout<<endl;
}
return 0;
}
|
Record.h
|
#ifndef RECORD__HH
#define RECORD__HH
#include<iostream>
#include<ctime>
#include<fstream>
#include<string>
#include<cstring>
#include<iomanip>
using namespace std;
class Record
{
public:
Record()
{
StartRecord();
}
void StartRecord() { startTime=clock(); } /*重置开始时间*/
void PrintCostTime()
{
curTime=clock();
cout<<(curTime-startTime)/1000;
}
private:
unsigned int startTime,curTime;
};
#endif
|
Rand.h
|
#ifndef RAND__HH__HH
#define RAND__HH__HH
#include<cstdlib>
#include<ctime>
using namespace std;
int RandIn(int left,int right)
{
if(left>=right)
return left;
int res=rand();
res=res%(right-left);
res+=left;
return res;
}
#endif
|
SelectKth.h
|
template <class T>
int SelectMiddle(T A[],int left,int right)
{
int middle=((left+right)>>1),p;
if( A[left]<A[middle] )
{
if(A[middle] <= A[right])
p=middle;
else //A[middle] is the biggest
p=(A[left] < A[right]) ? right :left;
}
else //A[left]>=A[middle]
{
if(A[right]>A[left])
p=left;
else //A[left] is the biggest
p=(A[middle]< A[right]) ? right :middle;
}
return p;
}
template <class T>
T SelectKth(T A[],int left,int right,int kth)
{
int i, store;
int p=SelectMiddle(A,left,right);
swap(A[p],A[right]);
store = left;
for (i = left; i < right; i++)
if (A[i] <= A[right])
swap(A[store++], A[i]);
swap(A[store], A[right]);
if(store+1==kth)
return A[store];
else if(store+1<kth)
return SelectKth(A,store+1,right,kth);
else //sotre+1>kth
return SelectKth(A,left,store-1,kth);
}
|
类别:算法 查看评论