Matrix
Description
Given an n*n matrix A, whose entries Ai,j are
integer numbers ( 0 <= i < n, 0 <= j < n ). An operation
SHIFT at row i ( 0 <= i < n ) will move the integers in the row
one position right, and the rightmost integer will wrap around to the
leftmost column.
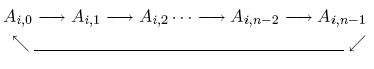
You can do the SHIFT operation at arbitrary row, and as many times
as you like. Your task is to minimize
max0<=j< n{Cj|Cj=Σ0<=i<
nAi,j}Input
The input consists of several test cases. The
first line of each test case contains an integer n. Each of the
following n lines contains n integers, indicating the matrix A. The
input is terminated by a single line with an integer −1. You may assume
that 1 <= n <= 7 and |Ai,j| < 104.
Output
For each test case,
print a line containing the minimum value of the maximum of column
sums.
Sample Input
2
4 6
3 7
3
1 2 3
4 5 6
7 8 9
-1
Sample Output
11
15
题意:对任意行可右移任意多次,求列和得最大值,使这个最大值最小。代码:
#include<stdio.h>
#define maxn 10
#define inf 1 << 29
int w[maxn][maxn], ans[maxn][maxn];
int n, pre;
void find(int depth)
{
int i, j, max;
for (i = 0; i < n; i++)
{
for (j = 0, max = 0; j < n; j++)
{
ans[depth][j] = ans[depth-1][j] + w[depth][(j-i+n)%n];
//printf("%d ", ans[depth][j]);
if (max < ans[depth][j])
{
max = ans[depth][j];
}
}//printf("\n");
if (n - 1 != depth)
{
find(depth+1);
}
else
{
if (pre > max)
{
pre = max;
}
}
}
}
int main()
{
int i, j;
while (scanf("%d", &n), n != -1)
{
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
scanf("%d", &w[i][j]);
}
}
pre = inf;
if (n > 1)
{
for (i = 0; i < n; i++)
{
ans[0][i] = w[0][i];
}
find(1);
}
else
{
pre = w[0][0];
}
printf("%d\n", pre);
}
return 0;
}