General Gee is the commander of a military base. He has just received alarming news from one of his spies: the enemy's preparing an air missile strike. The base contains two magnetic towers. When activated and given sufficient power, each of the magnetic towers creates a powerful horizontal magnetic disk. If any missile passes through this disk it deflects away from the base.
Although those towers seem to be an excellent air defense method, there is a problem: The area of the disk generated by a tower is proportional to the amount of energy it receives. The base has enough power plants to generate a certain amount of energy, which has to be divided among those two towers. That means that the total area of the two disks generated from the towers should not exceed the total energy generated by the power plants. Fortunately, the spy was able to know the exact target co-ordinates of the incoming missiles and he reported them to General Gee. The General needs your help in distributing the energy on the two magnetic towers to minimize the number of missiles that will not get deflected by the magnetic towers and therefore will hit the base. You may assume the following:
   1. The towers have different heights and therefore there are no problems associated with the magnetic disks interfering with each other.
   2. A missile will deflect if it passes through the magnetic disk of a tower or even if it just touches its boundary.
   3. A missile hitting a tower (landing exactly on its location) will deflect, even if the tower is not given any energy.
   4. All incoming missiles will go down simultaneously at the exact instant; therefore, there will not be any time available to redistribute the energy amongst the two towers during the strike.

Input consists of several test cases. Each test case is specified on N+2 lines. The first line contains an integer (1 <= N <= 1, 000) representing the number of missiles. The second line contains 5 real numbers X₁, Y₁, X₂, Y₂ and T: (X₁, Y₁) is the coordinates of the first tower, (X₂, Y₂) is the coordinates of the second tower and (0 <= T) is the total amount of energy generated from the power plants (the total area of the two magnetic disks). Each line of the remaining N lines contains two real numbers representing the landing coordinates of a missile.
The absolute value of all the given real numbers is less than or equal to 100 and may include a decimal point followed by up to 3 digits. Any two consecutive numbers on the same line are separated by one or more white-space characters. Zero or more blank lines may appear between test cases.
The last line of the input file is made of a single zero.

For each test case, print the following line:
k. M
Where k is the test case number (starting at one,) and M is the minimum number of missiles that will NOT be deflected in the best distribution of energy among the two towers. Use π = 3.141.
Note: There is a blank space before M.

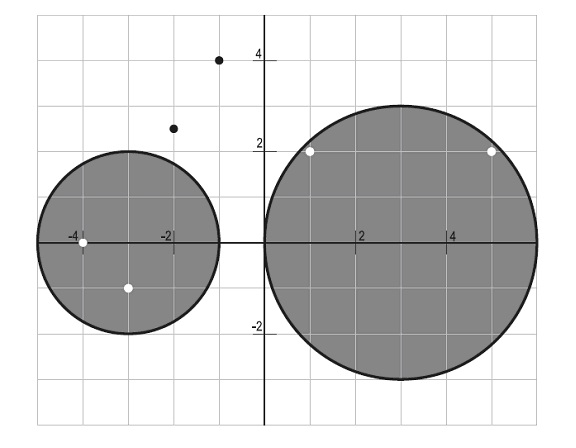
6
-3 0 3 0 40.833
-1 4
-2 2.5
1 2
5 2
-4 0
-3 -1
2
0 0 1 1 0
0 0
1 1
0

1. 2
2. 0

#include<stdio.h>
#include<stdlib.h>
#define maxn 1000
#define PI 3.141
const double inf = 0.00001;
double d1[maxn], d2[maxn];
double dis(double x1, double y1, double x2, double y2)
{
    return 1.0 * (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
int main()
{
    int n, i, j, ans, sum, k = 0;
    double r1, r2, r3, r4, r;
    double x1, y1, x2, y2, x, y;
    while (scanf("%d", &n), n)
    {
        scanf("%lf%lf%lf%lf%lf", &x1, &y1, &x2, &y2, &r);
        r = 1.0 * r / PI;
        for (i = 0; i < n; i++)
        {
            scanf("%lf%lf", &x, &y);
            d1[i] = dis(x, y, x1, y1);
            d2[i] = dis(x, y, x2, y2);
        }
        for (i = 0, ans = n; i < n; i++)
        {
            r1 = d1[i];
            if (r1 <= r)//枚举一个点和其中一个塔的距离r1,则剩下的磁波距离为r2
            {
                r2 = r - r1;
                for (j = 0, sum = 0; j < n; j++)
                {
                    if (d1[j] <= r1)
                    {
                        sum++;
                    }
                    else if (d2[j] <= r2)
                    {
                        sum++;
                    }
                }
                if (ans > n - sum)
                {
                    ans = n - sum;
                }
            }
            r2 = d2[i];
            if (r2 <= r)
            {
                r1 = r - r2;
                for (j = 0, sum = 0; j < n; j++)
                {
                    if (d1[j] <= r1)
                    {
                        sum++;
                    }
                    else if (d2[j] <= r2)
                    {
                        sum++;
                    }
                }
                if (ans > n - sum)
                {
                    ans = n - sum;
                }
            }
            
        }
        k++;
        printf("%d. %d\n", k, ans);
    }
    return 0;
}