Sorting Slides
Description
Professor
Clumsey is going to give an important talk this afternoon.
Unfortunately, he is not a very tidy person and has put all his
transparencies on one big heap. Before giving the talk, he has to sort
the slides. Being a kind of minimalist, he wants to do this with the
minimum amount of work possible.
The situation is like this. The slides all have numbers written on
them according to their order in the talk. Since the slides lie on each
other and are transparent, one cannot see on which slide each number is
written.
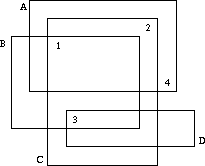
Well, one cannot see on which slide a number is written, but one
may deduce which numbers are written on which slides. If we label the
slides which characters A, B, C, ... as in the figure above, it is
obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
Input
The
input consists of several heap descriptions. Each heap descriptions
starts with a line containing a single integer n, the number of slides
in the heap. The following n lines contain four integers xmin, xmax,
ymin and ymax, each, the bounding coordinates of the slides. The slides
will be labeled as A, B, C, ... in the order of the input.
This is followed by n lines containing two integers each, the x-
and y-coordinates of the n numbers printed on the slides. The first
coordinate pair will be for number 1, the next pair for 2, etc. No
number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
Output
For
each heap description in the input first output its number. Then print
a series of all the slides whose numbers can be uniquely determined
from the input. Order the pairs by their letter identifier.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
Sample Input
4
6 22 10 20
4 18 6 16
8 20 2 18
10 24 4 8
9 15
19 17
11 7
21 11
2
0 2 0 2
0 2 0 2
1 1
1 1
0
Sample Output
Heap 1
(A,4) (B,1) (C,2) (D,3)
Heap 2
none
题意:有编号的幻灯片是透明的,叠在一起的时候,除了没被覆盖的编号,其他的编号被多张幻灯片覆盖时就分不清哪个编号是哪张的。
但能通过确定的幻灯片的编号(编号只被一张幻灯片覆盖,这个编号就是该幻灯片的)来用排除法确定其他幻灯片的编号。
求:是否能确定所有幻灯片的编号。如果可以,对每张幻灯片,判断这个编号是否是唯一的。对唯一编号幻灯片输出编号。
分析:这个直接是比较明显的二分图最大匹配。首先肯定是选取唯一确定的幻灯片不用,接下来就是交叉路径求可增光路的事了。整个过程就是匈牙利算法。
求出匹配方案M,对M中每次删除一个边,再次通过该边的一点看看是否有可增光路,有则会再次达到最大匹配,这说明该编号对应的可选矩形不唯一。
#include <iostream>
#define maxn 1000
using namespace std;
struct T
{
int x1, x2, y1, y2;
}reg[maxn];
int mat[maxn][maxn], hash[maxn], pre[maxn], path[maxn];
int n;
int more(int u)
{
int i;
for (i = 0; i < n; i++)
{
if (hash[i] == 0 && mat[u][i])
{
hash[i] = 1;
if (pre[i] == -1 || more(pre[i]))
{
pre[i] = u;
return 1;
}
}
}
return 0;
}
int eft()
{
int i, j, num;
for (i = 0; i < n; i++) pre[i] = -1;
for (i = 0, num = 0; i < n; i++)
{
for (j = 0; j < n; j++) hash[j] = 0;
if (more(i))
{
num++;
}
}
return num;
}
int main()
{
int i, j, x1, x2, y1, y2, x, y, num, sign, ca = 0, m;
while (scanf("%d", &n), n)
{
ca++;
for (i = 0; i < n; i++)
{
scanf("%d%d%d%d", ®[i].x1, ®[i].x2, ®[i].y1, ®[i].y2);
}
for (i = 0; i < n; i++)
{
scanf("%d%d", &x, &y);
for (j = 0; j < n; j++)//编号被幻灯片上覆盖的,编号跟其连边,表示该编号可能在该幻灯片上
{
if (x > reg[j].x1 && x < reg[j].x2 && y > reg[j].y1 && y < reg[j].y2)
{
mat[i][j] = 1;
}
else
{
mat[i][j] = 0;
}
}
}
num = eft();
sign = 0;
printf("Heap %d\n", ca);
if (num == n)//能找到一种方案让每个编号对应一个幻灯片
{
for (i = 0; i < n; i++)
{
path[i] = pre[i];
}
for (i = 0; i < n; i++)
{
mat[path[i]][i] = 0;//删边
if (eft() == num)//如果能再次达到最大匹配M,则编号跟幻灯片不是唯一的
{
continue;
}
else
{
if (sign)
{
printf(" ");
}
printf("(%c,%d)", 'A' + i, path[i] + 1);//否则,输出唯一对应的幻灯片跟编号。
sign = 1;
}
mat[path[i]][i] = 1;
}
}
if (!sign)
{
printf("none");
}
printf("\n\n");
}
return 0;
}