真是个讨厌的题目，输出及其猥琐。其他的点评，没了。
#include<iostream>
#include<cmath>
using namespace std;
const int maxn=100020;
int v[maxn];
int order[maxn];
int ans[maxn];//存放结果
int solve(int n,int m,int &pos)
{
memset(order,0,sizeof(order));
memset(v,0,sizeof(v));
int f=0;
int cnt=0;
v[n]=1;n*=10;
while(n)
{
if(v[n%m]==1)
{
f=1;ans[++cnt]=n/m;n%=m;
break;
}
else v[n%m]=1;
ans[++cnt]=n/m;
n%=m;
order[n]=cnt;
n*=10;
}
if(f==0)
pos=-1;
else pos=order[n];
return cnt;
}
int get(int n)
{
return log((double)n);
}
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF)
{
int cnt;
int pos;
if(n%m==0)
{
printf("%d.0\n",n/m);
continue;
}
int zhengshu=n/m;
n%=m;
int len=solve(n,m,pos);
if(zhengshu!=0)
cnt=get(zhengshu)+1;
else
cnt=2;
if(pos==-1)
{
printf("%d.",zhengshu);
for(int i=1;i<=len;i++)
{
printf("%d",ans[i]);
cnt++;
if(cnt%76==0)
printf("\n");
}
if(cnt%76!=0)
printf("\n");
}
else
{
printf("%d.",zhengshu);
for(int i=1;i<=pos;i++)
{
printf("%d",ans[i]);
cnt++;
if(cnt%76==0)
printf("\n");
}
printf("(");
cnt++;
if(cnt%76==0)
printf("\n");
for(int i=pos+1;i<=len;i++)
{
printf("%d",ans[i]);
cnt++;
if(cnt%76==0)
printf("\n");
}
printf(")");
cnt++;
if(cnt%76==0)
printf("\n");
if(cnt%76!=0)
printf("\n");
}
}
return 0;
}
世界的每一个角落，
都埋藏着对中国人的疑问。
路在问，树在问，
窗后的眼睛都在问：
你们，究竟是什么人？
太长的岁月是否积累了太多的计谋？
太多的人口是否潜伏着威胁的可能？
你们是否尔虞我诈？
你们是否尊重人性？
我一次次讲解，
一次次辩论，
他们总是礼貌地点头，
却又转向了别的传闻。
在远方的街道我曾暗暗自语：
既然人家不信，
那又何必伤心？
他们有他们的偏见，
我们有我们的毛病。
终于，
一次自然地震引发了精神地震，
一场惊世天灾掀去了远年蒙尘，
一条地壳裂缝透露了事实真相，
一批中国地名擦亮了世界的眼睛。
历史上居然会有这样一个时刻，
十几亿人的眼泪汇流成了一个爱字；
地球上居然会有这样一个角落，
十几亿人的心思全在废墟下的生命。
空前拥挤的天空，
空前拥挤的险径，
空前奔涌的血液，
空前奔涌的呼声，
全在表达着一种文明，
以及它延续至今的原因。
对于飞来横祸，再骄傲的民族也很难作出一致的反应，
对于生离死别，再高雅的人群也很难设计动人的表情。
那么，这次，
请看中国的反应，中国的表情！
毫不预警下的透明呈现，
只能是中华民族的自然本性。
远方的朋友终于看清了吧？
这就是中国人。
在全民肃立的哀悼日我又暗暗自语：
如果能有十个轮回，
即使再有海啸地震，
我已别无选择，
永远在这里投生！
RT,突然感觉到人生面临的巨大的危机感。我想，ACM这个东西，可能我需要告别你一段时间了，不过请相信我，我们还会再见面。
当AH=0EH
这个子程序是使显示器像打字机一样的显示字符来，在前面用 AH=09H/INT 10H 和 AH=0AH/INT 10H 都可以在萤光幕上显示字符，但是这两奘方式显示字符之后，光标位置并不移动，而 AH=0EH/INT 10H 则会使光标位置移动，每显示一个字符，光标会往右移一格，假如已经到最右边了，则光标会移到最左边并移到下一列，假如已经移到最下面一列的最右边，则屏幕会向上卷动。
AL 寄存器存要显示的字符，BH 为目前的显示页，如果是在图形模式，则 BH 须设为 0，假如是在图形模式下，也可以设定 BL 来表示文字的颜色，文字模式下的 BL 则无功能。
好像目前还没有这方面题目的总结。这几天连续看到四个问这类题目的人，今天在这里简单写一下。这里我们不介绍其它有关矩阵的知识，只介绍矩阵乘法和相关性质。
不要以为数学中的矩阵也是黑色屏幕上不断变化的绿色字符。在数学中，一个矩阵说穿了就是一个二维数组。一个n行m列的矩阵可以乘以一个m行p列的矩阵，得到的结果是一个n行p列的矩阵，其中的第i行第j列位置上的数等于前一个矩阵第i行上的m个数与后一个矩阵第j列上的m个数对应相乘后所有m个乘积的和。比如，下面的算式表示一个2行2列的矩阵乘以2行3列的矩阵，其结果是一个2行3列的矩阵。其中，结果的那个4等于2*2+0*1：
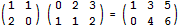
下面的算式则是一个1 x 3的矩阵乘以3 x 2的矩阵，得到一个1 x 2的矩阵：
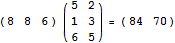
矩阵乘法的两个重要性质：一，矩阵乘法
不满足交换律；二，矩阵乘法满足结合律。为什么矩阵乘法不满足交换律呢？废话，交换过来后两个矩阵有可能根本不能相乘。为什么它又满足结合律呢？仔细想想你会发现这也是废话。假设你有三个矩阵A、B、C，那么(AB)C和A(BC)的结果的第i行第j列上的数都等于所有A(ik)*B(kl)*C(lj)的和（枚举所有的k和l）。
经典题目1 给定n个点，m个操作，构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转 这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转（两种情况），旋转则以原点为中心。如果对每个点分别进行模拟，那么m个操作总共耗时O(mn)。利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵，然后每个点与该矩阵相乘即可直接得出最终该点的位置，总共耗时O(m+n)。假设初始时某个点的坐标为x和y，下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。预先把所有m个操作所对应的矩阵全部乘起来，再乘以(x,y,1)，即可一步得出最终点的位置。
经典题目2 给定矩阵A，请快速计算出A^n（n个A相乘）的结果，输出的每个数都mod p。 由于矩阵乘法具有结合律，因此A^4 = A * A * A * A = (A*A) * (A*A) = A^2 * A^2。我们可以得到这样的结论：当n为偶数时，A^n = A^(n/2) * A^(n/2)；当n为奇数时，A^n = A^(n/2) * A^(n/2) * A （其中n/2取整）。这就告诉我们，计算A^n也可以使用二分快速求幂的方法。例如，为了算出A^25的值，我们只需要递归地计算出A^12、A^6、A^3的值即可。根据
这里的一些结果，我们可以在计算过程中不断取模，避免高精度运算。
经典题目3 POJ3233 (感谢
rmq)
题目大意：给定矩阵A，求A + A^2 + A^3 + ... + A^k的结果（两个矩阵相加就是对应位置分别相加）。输出的数据mod m。k<=10^9。
这道题两次二分，相当经典。首先我们知道，A^i可以二分求出。然后我们需要对整个题目的数据规模k进行二分。比如，当k=6时，有：
A + A^2 + A^3 + A^4 + A^5 + A^6 =
(A + A^2 + A^3) + A^3*
(A + A^2 + A^3) 应用这个式子后，规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3，即可得到原问题的答案。
经典题目4 VOJ1049 题目大意：顺次给出m个置换，反复使用这m个置换对初始序列进行操作，问k次置换后的序列。m<=10, k<2^31。
首先将这m个置换“合并”起来（算出这m个置换的乘积），然后接下来我们需要执行这个置换k/m次（取整，若有余数则剩下几步模拟即可）。注意任意一个置换都可以表示成矩阵的形式。例如，将1 2 3 4置换为3 1 2 4，相当于下面的矩阵乘法：
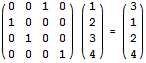
置换k/m次就相当于在前面乘以k/m个这样的矩阵。我们可以二分计算出该矩阵的k/m次方，再乘以初始序列即可。做出来了别忙着高兴，得意之时就是你灭亡之日，别忘了最后可能还有几个置换需要模拟。
经典题目5 《算法艺术与信息学竞赛》207页（2.1代数方法和模型，[例题5]细菌，版次不同可能页码有偏差） 大家自己去看看吧，书上讲得很详细。解题方法和上一题类似，都是用矩阵来表示操作，然后二分求最终状态。
经典题目6 给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31 根据前面的一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵，这两个数就会多迭代一次。那么，我们把这个2 x 2的矩阵自乘n次，再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想，这个2 x 2的矩阵很容易构造出来：
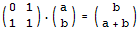经典题目7 VOJ1067 我们可以用上面的方法二分求出任何一个线性递推式的第n项，其对应矩阵的构造方法为：在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1，矩阵第n行填对应的系数，其它地方都填0。例如，我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项：
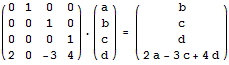
利用矩阵乘法求解线性递推关系的题目我能编出一卡车来。这里给出的例题是系数全为1的情况。
经典题目8 给定一个有向图，问从A点恰好走k步（允许重复经过边）到达B点的方案数mod p的值 把给定的图转为邻接矩阵，即A(i,j)=1当且仅当存在一条边i->j。令C=A*A，那么C(i,j)=ΣA(i,k)*A(k,j)，实际上就等于从点i到点j恰好经过2条边的路径数（枚举k为中转点）。类似地，C*A的第i行第j列就表示从i到j经过3条边的路径数。同理，如果要求经过k步的路径数，我们只需要二分求出A^k即可。
经典题目9 用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案，M<=5，N<2^31，输出答案mod p的结果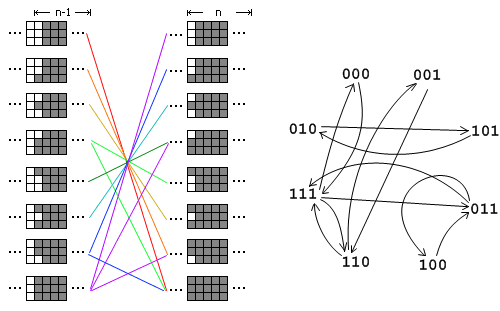 
我们以M=3为例进行讲解。假设我们把这个矩形横着放在电脑屏幕上，从右往左一列一列地进行填充。其中前n-2列已经填满了，第n-1列参差不齐。现在我们要做的事情是把第n-1列也填满，将状态转移到第n列上去。由于第n-1列的状态不一样（有8种不同的状态），因此我们需要分情况进行讨论。在图中，我把转移前8种不同的状态放在左边，转移后8种不同的状态放在右边，左边的某种状态可以转移到右边的某种状态就在它们之间连一根线。注意为了保证方案不重复，状态转移时我们不允许在第n-1列竖着放一个多米诺骨牌（例如左边第2种状态不能转移到右边第4种状态），否则这将与另一种转移前的状态重复。把这8种状态的转移关系画成一个有向图，那么问题就变成了这样：从状态111出发，恰好经过n步回到这个状态有多少种方案。比如，n=2时有3种方案，111->011->111、111->110->111和111->000->111，这与用多米诺骨牌覆盖3x2矩形的方案一一对应。这样这个题目就转化为了我们前面的例题8。
后面我写了一份此题的源代码。你可以再次看到位运算的相关应用。
经典题目10 POJ2778 题目大意是，检测所有可能的n位DNA串有多少个DNA串中不含有指定的病毒片段。合法的DNA只能由ACTG四个字符构成。题目将给出10个以内的病毒片段，每个片段长度不超过10。数据规模n<=2 000 000 000。
下面的讲解中我们以ATC,AAA,GGC,CT这四个病毒片段为例，说明怎样像上面的题一样通过构图将问题转化为例题8。我们找出所有病毒片段的前缀，把n位DNA分为以下7类：以AT结尾、以AA结尾、以GG结尾、以?A结尾、以?G结尾、以?C结尾和以??结尾。其中问号表示“其它情况”，它可以是任一字母，只要这个字母不会让它所在的串成为某个病毒的前缀。显然，这些分类是全集的一个划分（交集为空，并集为全集）。现在，假如我们已经知道了长度为n-1的各类DNA中符合要求的DNA个数，我们需要求出长度为n时各类DNA的个数。我们可以根据各类型间的转移构造一个边上带权的有向图。例如，从AT不能转移到AA，从AT转移到??有4种方法（后面加任一字母），从?A转移到AA有1种方案（后面加个A），从?A转移到??有2种方案（后面加G或C），从GG到??有2种方案（后面加C将构成病毒片段，不合法，只能加A和T）等等。这个图的构造过程类似于用有限状态自动机做串匹配。然后，我们就把这个图转化成矩阵，让这个矩阵自乘n次即可。最后输出的是从??状态到所有其它状态的路径数总和。
题目中的数据规模保证前缀数不超过100，一次矩阵乘法是三方的，一共要乘log(n)次。因此这题总的复杂度是100^3 * log(n)，AC了。
最后给出第9题的代码供大家参考（今天写的，熟悉了一下C++的类和运算符重载）。为了避免大家看代码看着看着就忘了，我把这句话放在前面来说：
Matrix67原创，转贴请注明出处。
#include <cstdio>
#define SIZE (1<<m)
#define MAX_SIZE 32
using namespace std;
class CMatrix
{
public:
long element[MAX_SIZE][MAX_SIZE];
void setSize(int);
void setModulo(int);
CMatrix operator* (CMatrix);
CMatrix power(int);
private:
int size;
long modulo;
};
void CMatrix::setSize(int a)
{
for (int i=0; i<a; i++)
for (int j=0; j<a; j++)
element[i][j]=0;
size = a;
}
void CMatrix::setModulo(int a)
{
modulo = a;
}
CMatrix CMatrix::operator* (CMatrix param)
{
CMatrix product;
product.setSize(size);
product.setModulo(modulo);
for (int i=0; i<size; i++)
for (int j=0; j<size; j++)
for (int k=0; k<size; k++)
{
product.element[i][j]+=element[i][k]*param.element[k][j];
product.element[i][j]%=modulo;
}
return product;
}
CMatrix CMatrix::power(int exp)
{
CMatrix tmp = (*this) * (*this);
if (exp==1) return *this;
else if (exp & 1) return tmp.power(exp/2) * (*this);
else return tmp.power(exp/2);
}
int main()
{
const int validSet[]={0,3,6,12,15,24,27,30};
long n, m, p;
CMatrix unit;
scanf("%d%d%d", &n, &m, &p);
unit.setSize(SIZE);
for(int i=0; i<SIZE; i++)
for(int j=0; j<SIZE; j++)
if( ((~i)&j) == ((~i)&(SIZE-1)) )
{
bool isValid=false;
for (int k=0; k<8; k++)isValid=isValid||(i&j)==validSet[k];
unit.element[i][j]=isValid;
}
unit.setModulo(p);
printf("%d", unit.power(n).element[SIZE-1][SIZE-1] );
return 0;
} 源地址：
http://www.matrix67.com/blog/?s=%E5%8D%81%E4%B8%AA%E5%88%A9%E7%94%A8%E7%9F%A9%E9%98%B5%E4%B9%98%E6%B3%95%E8%A7%A3%E5%86%B3%E7%9A%84%E7%BB%8F%E5%85%B8%E9%A2%98%E7%9B%AE
摘要: 没想到这个暴力题让我郁闷了半小时，最后发现原来是回溯的问题。基本功不扎实啊。。。
#include<iostream>#include<cstring>using namespace std;int n;int v[200];int order[200];struct node{ ...
阅读全文
题意：P(x)=x各个数字位的乘积。x<=10^1000，求min{ans|ans>x && P(ans)=P(x)}。
显然如果x的数字位含有0，分两种情况：
1）：只有一个0，如果0在个位数，那么x+10就是最优解了。如果0不在个位数，则x+1就是最优解。
2）：有2个或2个以上的0，那么x+1就是最优解。
证明略，很容易看出的。
接下来就是处理不含0的情况。
把x的各个数字位分解质因子。只有2,3,5,7这4个素数。
然后从高位深搜解，这里有加些剪枝。就是在搜索的时候每步都有保证搜到的解>=x。这样的话就会很快的搜到最优解。具体实现就是设一个flag值，flag为真表示当前搜的解>x否则=x。如果flag为真，则改数字位从1开始搜到9，如果flag不为真，则改状态的数字位从x原本的数字位开始搜，只要碰到改状态的数字大于原本的数字位就要改flag为真。这样就可以保证比较快的搜到解了。然后随便在了点杂七杂八的剪枝就差不多了。
最后还要在判断刚才的搜索有没有找到解，如果没有找到解，那么只剩一种情况了，就是增加一个数字位'1'；排序，输出。
我的搜索已经写的很暴力了，str函数狂用，用时10ms。
不知道有没有更高效的做法，或者有直接更妙的构造方法呢？
——by yayamao
先看费马小定理：
费马小定理是
数论中的一个重要定理,其内容为:
假如p是质数，且(a,p)=1，那么 a^(p-1) ≡１（mod p）
假如p是质数，且a,p互质，那么 a的(p-1)次方除以p的余数恒等于1
逆元：
设m为正整数，a为正整数，如果存在a' 使得：
a X a' = 1（mod m）
a'叫做a的逆元。密码学中用到了这个结论。RSA.
证明:x^(MOD-1) = 1 (mod MOD)
x*x^(MOD-2) = 1 (mod MOD) x^(MOD-2)为其逆元
其中MOD 为素数 ， x要小于MOD,如果x>=MOD,可以先对x取MOD,这不会影响结果。
另一种想法：
其实用莫线性方程解a'亦可。 扩展欧几里德...
摘要: 就是写得太长了 可以更精简些的
#include <iostream> using namespace std; class CFraction { private: &nbs...
阅读全文