#
高斯消元法,是线性代数中的一个算法,可用来求解线性方程组,并可以求出矩阵的秩,以及求出可逆方阵的逆矩阵。
高斯消元法的原理是:
若用初等行变换将增广矩阵 化为 ,则AX = B与CX = D是同解方程组。
所以我们可以用初等行变换把增广矩阵转换为行阶梯阵,然后回代求出方程的解。
以上是线性代数课的回顾,下面来说说高斯消元法在编程中的应用。
首先,先介绍程序中高斯消元法的步骤:
(我们设方程组中方程的个数为equ,变元的个数为var,注意:一般情况下是n个方程,n个变元,但是有些题目就故意让方程数与变元数不同)
1. 把方程组转换成增广矩阵。
2. 利用初等行变换来把增广矩阵转换成行阶梯阵。
枚举k从0到equ – 1,当前处理的列为col(初始为0) ,每次找第k行以下(包括第k行),col列中元素绝对值最大的列与第k行交换。如果col列中的元素全为0,那么则处理col + 1列,k不变。
3. 转换为行阶梯阵,判断解的情况。
① 无解
当方程中出现(0, 0, …, 0, a)的形式,且a != 0时,说明是无解的。
② 唯一解
条件是k = equ,即行阶梯阵形成了严格的上三角阵。利用回代逐一求出解集。
③ 无穷解。
条件是k < equ,即不能形成严格的上三角形,自由变元的个数即为equ – k,但有些题目要求判断哪些变元是不缺定的。
这里单独介绍下这种解法:
首先,自由变元有var - k个,即不确定的变元至少有var - k个。我们先把所有的变元视为不确定的。在每个方程中判断不确定变元的个数,如果大于1个,则该方程无法求解。如果只有1个变元,那么该变元即可求出,即为确定变元。
以上介绍的是求解整数线性方程组的求法,复杂度是O(n3)。浮点数线性方程组的求法类似,但是要在判断是否为0时,加入EPS,以消除精度问题。
下面讲解几道OJ上的高斯消元法求解线性方程组的题目:
POJ 1222 EXTENDED LIGHTS OUT
http://acm.pku.edu.cn/JudgeOnline/problem?id=1222
POJ 1681 Painter's Problem
http://acm.pku.edu.cn/JudgeOnline/problem?id=1681
POJ 1753 Flip Game
http://acm.pku.edu.cn/JudgeOnline/problem?id=1753
POJ 1830 开关问题
http://acm.pku.edu.cn/JudgeOnline/problem?id=1830
POJ 3185 The Water Bowls
http://acm.pku.edu.cn/JudgeOnline/problem?id=3185
开关窗户,开关灯问题,很典型的求解线性方程组的问题。方程数和变量数均为行数*列数,直接套模板求解即可。但是,当出现无穷解时,需要枚举解的情况,因为无法判断哪种解是题目要求最优的。
POJ 2947 Widget Factory
http://acm.pku.edu.cn/JudgeOnline/problem?id=2947
求解同余方程组问题。与一般求解线性方程组的问题类似,只要在求解过程中加入取余即可。
注意:当方程组唯一解时,求解过程中要保证解在[3, 9]之间。
POJ 1166 The Clocks
http://acm.pku.edu.cn/JudgeOnline/problem?id=1166
经典的BFS问题,有各种解法,也可以用逆矩阵进行矩阵相乘。
但是这道题用高斯消元法解决好像有些问题(困扰了我N天...持续困扰中...),由于周期4不是素数,故在求解过程中不能进行取余(因为取余可能导致解集变大),但最后求解集时,还是需要进行取余操作,那么就不能保证最后求出的解是正确的...在discuss里提问了好几天也没人回答...希望哪位路过的大牛指点下~~
POJ 2065 SETI
http://acm.pku.edu.cn/JudgeOnline/problem?id=2065
同样是求解同余方程组问题,由于题目中的p是素数,可以直接在求解时取余,套用模板求解即可。(虽然AC的人很少,但它还是比较水的一道题,)
POJ 1487 Single-Player Games
http://acm.pku.edu.cn/JudgeOnline/problem?id=1487
很麻烦的一道题目...题目中的叙述貌似用到了编译原理中的词法定义(看了就给人不想做的感觉...)
解方程组的思想还是很好看出来了(前提是通读题目不下5遍...),但如果把树的字符串表达式转换成方程组是个难点,我是用栈 + 递归的做法分解的。首先用栈的思想求出该结点的孩子数,然后递归分别求解各个孩子。
这题解方程组也与众不同...首先是求解浮点数方程组,要注意精度问题,然后又询问不确定的变元,按前面说的方法求解。
一顿折腾后,这题居然写了6000+B...而且囧的是巨人C++ WA,G++ AC,可能还是精度的问题吧...看这题目,看这代码,就没有改的欲望...
hdu OJ 2449
http://acm.hdu.edu.cn/showproblem.php?pid=2449
哈尔滨现场赛的一道纯高斯题,当时鹤牛敲了1个多小时...主要就是写一个分数类,套个高精模板(偷懒点就Java...)搞定~~
注意下0和负数时的输出即可。
fze OJ 1704
http://acm.fzu.edu.cn/problem.php?pid=1704
福大月赛的一道题目,还是经典的开关问题,但是方程数和变元数不同(考验模板的时候到了~~),最后要求增广阵的阶,要用到高精度~~
Sgu 275 To xor or not to xor
http://acm.sgu.ru/problem.php?contest=0&problem=275
题解:
http://hi.baidu.com/czyuan%5Facm/blog/item/be3403d32549633d970a16ee.html
这里提供下自己写的还算满意的求解整数线性方程组的模板(浮点数类似,就不提供了)~~
/* 用于求整数解得方程组. */
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
const int maxn = 105;
int equ, var; // 有equ个方程,var个变元。增广阵行数为equ, 分别为0到equ - 1,列数为var + 1,分别为0到var.
int a[maxn][maxn];
int x[maxn]; // 解集.
bool free_x[maxn]; // 判断是否是不确定的变元.
int free_num;
void Debug(void)
{
int i, j;
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
inline int gcd(int a, int b)
{
int t;
while (b != 0)
{
t = b;
b = a % b;
a = t;
}
return a;
}
inline int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
// 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解,但无整数解,-1表示无解,0表示唯一解,大于0表示无穷解,并返回自由变元的个数)
int Gauss(void)
{
int i, j, k;
int max_r; // 当前这列绝对值最大的行.
int col; // 当前处理的列.
int ta, tb;
int LCM;
int temp;
int free_x_num;
int free_index;
// 转换为阶梯阵.
col = 0; // 当前处理的列.
for (k = 0; k < equ && col < var; k++, col++)
{ // 枚举当前处理的行.
// 找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)
max_r = k;
for (i = k + 1; i < equ; i++)
{
if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i;
}
if (max_r != k)
{ // 与第k行交换.
for (j = k; j < var + 1; j++) swap(a[k][j], a[max_r][j]);
}
if (a[k][col] == 0)
{ // 说明该col列第k行以下全是0了,则处理当前行的下一列.
k--; continue;
}
for (i = k + 1; i < equ; i++)
{ // 枚举要删去的行.
if (a[i][col] != 0)
{
LCM = lcm(abs(a[i][col]), abs(a[k][col]));
ta = LCM / abs(a[i][col]), tb = LCM / abs(a[k][col]);
if (a[i][col] * a[k][col] < 0) tb = -tb; // 异号的情况是两个数相加.
for (j = col; j < var + 1; j++)
{
a[i][j] = a[i][j] * ta - a[k][j] * tb;
}
}
}
}
Debug();
// 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
for (i = k; i < equ; i++)
{ // 对于无穷解来说,如果要判断哪些是自由变元,那么初等行变换中的交换就会影响,则要记录交换.
if (a[i][col] != 0) return -1;
}
// 2. 无穷解的情况: 在var * (var + 1)的增广阵中出现(0, 0, ..., 0)这样的行,即说明没有形成严格的上三角阵.
// 且出现的行数即为自由变元的个数.
if (k < var)
{
// 首先,自由变元有var - k个,即不确定的变元至少有var - k个.
for (i = k - 1; i >= 0; i--)
{
// 第i行一定不会是(0, 0, ..., 0)的情况,因为这样的行是在第k行到第equ行.
// 同样,第i行一定不会是(0, 0, ..., a), a != 0的情况,这样的无解的.
free_x_num = 0; // 用于判断该行中的不确定的变元的个数,如果超过1个,则无法求解,它们仍然为不确定的变元.
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j;
}
if (free_x_num > 1) continue; // 无法求解出确定的变元.
// 说明就只有一个不确定的变元free_index,那么可以求解出该变元,且该变元是确定的.
temp = a[i][var];
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && j != free_index) temp -= a[i][j] * x[j];
}
x[free_index] = temp / a[i][free_index]; // 求出该变元.
free_x[free_index] = 0; // 该变元是确定的.
}
return var - k; // 自由变元有var - k个.
}
// 3. 唯一解的情况: 在var * (var + 1)的增广阵中形成严格的上三角阵.
// 计算出Xn-1, Xn-2 ... X0.
for (i = var - 1; i >= 0; i--)
{
temp = a[i][var];
for (j = i + 1; j < var; j++)
{
if (a[i][j] != 0) temp -= a[i][j] * x[j];
}
if (temp % a[i][i] != 0) return -2; // 说明有浮点数解,但无整数解.
x[i] = temp / a[i][i];
}
return 0;
}
int main(void)
{
freopen("Input.txt", "r", stdin);
int i, j;
while (scanf("%d %d", &equ, &var) != EOF)
{
memset(a, 0, sizeof(a));
memset(x, 0, sizeof(x));
memset(free_x, 1, sizeof(free_x)); // 一开始全是不确定的变元.
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
scanf("%d", &a[i][j]);
}
}
// Debug();
free_num = Gauss();
if (free_num == -1) printf("无解!\n");
else if (free_num == -2) printf("有浮点数解,无整数解!\n");
else if (free_num > 0)
{
printf("无穷多解! 自由变元个数为%d\n", free_num);
for (i = 0; i < var; i++)
{
if (free_x[i]) printf("x%d 是不确定的\n", i + 1);
else printf("x%d: %d\n", i + 1, x[i]);
}
}
else
{
for (i = 0; i < var; i++)
{
printf("x%d: %d\n", i + 1, x[i]);
}
}
printf("\n");
}
return 0;
}
转自:http://hi.baidu.com/czyuan_acm/blog/item/ebf41f8fdc0e1ee6f01f36e9.html

Sometimes the most important history, is the history we are making today~
听说电视连续剧《蜗居》被禁了,据说是因为台词有点黄。果真如此吗?带着好奇,我从网上在线看了《蜗居》。一集一集地、认认真真地看了一遍。边看边同情、边看边感叹,边看边思考。不把心里的话说出来,我闷得慌。
我看《蜗居》的被禁,跟台词黄不黄没关系,大多是个禁它的借口。再热播下去,怕要出大乱子。一个月来,这部电视剧引起了很多人的关注和网上的热烈讨论。它将镜头对准了大城市中不那么光鲜的一面:房价的上涨以及由此给年轻人的理想造成的巨大冲击。我们自己的生活就像剧中描写的一样,一切都暴露在了阳光下。剧中把房子带来的社会问题推上极致,这种残酷的生活直抵每一个因房价而困扰生活的人。
一项36万多人参加的投票调查中,大多数人认为“幸福与房子关联密切。” “还房贷、吃盒饭”,已经成为房价飙升年代对白领生存状况的一种直白描摹。主人公一波三折的买房奋斗史,道出了都市无房族的困惑:房价是“一匹脱缰的野马”,攒钱的速度永远赶不上房价上涨的速度。
有人甘心做房奴吗,不买房子不行吗?答案是,不行!谁会租房租一辈子?你要说,没钱你就去郊区甚至农村买房子呀。对,可以在郊区或农村买到便宜房子,可是你的工作单位在市区,你怎么办?是啊,人民有广泛的自由,有选择的权利。可是,你要上学,就得接受高学费,你要看病就得接受高收费,你要住房就要选择高房价,除非你不让孩子上学、不去看病,不住房子。你有不选择的自由吗?没有。买房是社会逼的,是形势逼的,是必需的,你可以选择这,选择那,你能选择不住房子吗!
那,是谁逼着群众做了房奴?是垄断阶层,是官商勾结,是政治腐败!国家是人民的,资源是国家的,理应由人民共享。可是利益集团利用人民的资源,凭借其垄断地位要挟人民。看看现实,看看中石油、中石化, 领着巨额财政补贴,买楼是10亿10亿的买,不涨价就断你车子的油、不涨价就断你家的气,人为制造紧张。中国移动,传播黄色淫秽网络的先锋,哪里还有一丁点的社会责任;有线电视,大家都看见了,独此一家,不用也得用,不允许你安装卫星电视,查处你!诸如此类,实在太多。还有无耻的专家为他们摇旗呐喊:不能因为穷人喝不起水就不涨水价,中国的电价严重偏低。涨价是为了节约资源,更好地服务于人民,能力外的资本为零,哈哈,令人笑掉大牙……见过无耻的,没见过这么无耻的。
看看剧情吧,权力支配一切,资本动摇人性,利益逼良为娼。权贵阶层可以随便劫人祖居、淫人妻女、左右一切。同样是过年,富人在富丽堂皇充满温馨的大房子里,穷人没水没电点着蜡烛苦熬;群众顶着加班的压力努力地工作,不过取得些微薄的收入,而权贵的二奶买件衣服随便一出手就成千上万!这是我们要的和谐社会吗?
看到第19集,我,一个男人,哭了。小贝的几声大吼,你以为只是因为夺妻之恨吗?非也,他喊出了人压抑已久的东西!
感谢《蜗居》的七个理由?
上海电视台制作的35集电视连续剧《蜗居》在国家广电总局的否认禁播中还是被“禁播”了。只有上海东方卫视似乎还在播放,不过,大家多数人已经看过这部电视剧了,原因是网络拉近了精神产品制造者与消费者的距离。各地方电视台电视台形式上的禁播,只是一些人的作秀。我觉得应该感谢《蜗居》。
感谢《蜗居》的第一个理由,它引起争议。对《蜗居》的争议恐怕还要持续下去,就让发展见证或者证明它的必要与否吧!一部有争议的电视剧起码说明它是有关注度的,在被受众的关注过程中,既实现了电视台的播放价值,又实现了媒体的报道价值,还能教育国人,净化心灵。在对《蜗居》的争议中,国人慢慢接受它的存在。
感谢《蜗居》的第二理由,它没有乱伦。如今,国人已经出离了羞耻的地步,亲情、友情(同事情、战友情)、爱情等这些永恒的主题已经有了重新阐释的必要和必须了!而《蜗居》紧紧把握社会伦理道德的底线,没有让姐夫与小姨子发生任何关系,也没有通过更进一步的乱伦实现让受众关注的目的,这让一些人感动。
感谢《蜗居》的第三个理由,它写了拆迁。随着城市化进程的加速发展,随着国家拉动内需政策的深入执行,城市要扩展生存空间,老旧小区以及棚户区、平房、贫民区等都要被拆迁建新的。《蜗居》把存在于拆迁中的核心问题全部写出来,让观众自己感受,让观众自己解决。不管是利益拆迁还是流氓阻迁,都在观众的心理。
感谢《蜗居》的第四个理由,它痛恨腐败。腐败是发展的毒瘤,国人恨之入骨,尤其是哪些家中或者亲戚中没有当官的人,更是恨不得“吃腐败分子的肉,喝腐败分子的血”。当然,家中或者亲戚中如果有当官的腐败了,那就另当别论了!他们会以此自诩,同时,也会捞取一些提高生活水平的金钱、名誉、地位,彻底揭示出国人的双重人格。
感谢《蜗居》的第五个理由,它落笔于被社会遗忘的角落。过去组成社会机构的农民、工人、知识分子、商人的阶层,现在已经发生了极大的变化:农民(农民工、农电工)、公务员、工人(矿工)、企业员工、知识分子(教师)、领导干部……这些群体都有关注,也有代言人,也有说话的地方,而有一个群体是没有代言人的,是被遗忘的快要发霉的群体,他们生活在城市夹缝中喘不过起来,他们以打工名义无尽地奋斗着,他们是知识分子,他们有文化,有志向,有力气,有理想,就是没有跳起来高飞的平台。他们每天在一个企业里面被老板残忍的剥夺着,得到的与自己付出的根本不等价,他们的收入被以奉献的名义剥夺了,加班合理化、扣钱流氓化、养老保险强制化……就是打个车还要为城市管理者的无能埋单。
感谢《蜗居》的第六个理由,它关注士阶层。记得在中学的时候学习历史,讲到三国两晋南北朝时期,东晋出现了士阶层,他们有钱有势,生活无聊,寻找刺激,没有追求,攀比成风,人乳宴就是那个时候发明并且被推广起来的。现在这个新士阶层是一个高度变态的阶层,他们比谁的二奶奶多,脸蛋漂亮,岁数小……并且他们不会受到内心的谴责的,这是可怕的警示。
感谢《蜗居》的第七个理由,它打造忍者神龟。好像动画片里有个东西叫忍者神龟,《蜗居》就是告诉受众,在这个社会生活、生存必须学会忍让,就像乌龟那样永远地蜷缩着自己的脑袋,不要放出了。这样下去,将让这个社会失去了血性。
来看看猫扑网收集到的MOPPER的回复吧
这个电视剧恶攻精蝇的房地产政策!
没看过,但是被禁播一定有它的理由。毕竟话语权在精英手中。
似乎东方卫视还在播。
这是我们要的和谐社会吗?
哀民生之多艰!恨权贵之贪婪!怒官员之腐败!愧我party之怠慢!
资本主义社会,有多少钱,就有多少自由。你以为法律不禁止,你就自由了?
看到第19集,我,一个男人,哭了。小贝的几声大吼,你以为只是因为夺妻之恨吗?非也,他喊出了人压抑已久的东西!
以人为本。以人为本。以人为本。
触目惊心_____
权贵的二奶买件衣服随便一出手就成千上万!这是我们要的和谐社会吗?
富人在富丽堂皇充满温馨的大房子里,穷人没水没电点着蜡烛苦熬;群众顶着加班的压力努力地工作,不过取得些微薄的收入
看看剧情吧,权力支配一切,资本动摇人性,利益逼良为娼。权贵阶层可以随便劫人祖居、淫人妻女、左右一切
无耻的专家为他们摇旗呐喊:不能因为穷人喝不起水就不涨水价,中国的电价严重偏低。涨价是为了节约资源
不涨价就断你车子的油、不涨价就断你家的气,人为制造紧张。中国移动,传播黄色淫秽网络的先锋,哪里还有一丁点的社会责任
利益集团利用人民的资源,凭借其垄断地位要挟人民。看看现实,看看中石油、中石化, 领着巨额财政补贴,买楼是10亿10亿的买
是谁逼着群众做了房奴?是垄断阶层,是官商勾结,是政治腐败!国家是人民的,资源是国家的,理应由人民共享。
见过无耻的,没见过这么无耻的
社会会崩溃吗?房地产很可能就是de-tona-tor.
极有可能,动迁的,上访的,买不起房的,买房被套的,为房当二奶的........每个故事背后都是de-tona-tor,都和房地产有关.........
这样呵,我也去看看吧。
别当真,其实,其色情度,远不如……手机黄段子。关键的“错误”是……歌颂二奶,大奶很生气!
盛世危言。
《蜗居》很滥,不过目前中国……就是这么滥。滥点,一是作者滥情,二是房市滥市,三是官员滥政,四是女性滥性。
——转自天涯
摘要: 这题最简单的方法居然是暴力。。。时间复杂度一算大概是N^2,AC了。。。
#include<iostream>#include<cstdio>#include<cstring>using namespace std;//暴力求因子,打表 int n;int a[1000001],b[1000001]={0},c...
阅读全文
摘要: 这个题我是用线段树来做的,结果居然是超时。。。后来foreverlin同学告诉我他用树状数组过的,但我记得树状数组能解决的问题,线段树一定能解决,而且线段树的复杂度是logL级别,为什么我会超时呢?还请各位大牛指点。。。我的代码如下:
#include<iostream>#include<cstdio>#include<cstring>#include<...
阅读全文
久客逢馀闰,他乡别故人。自然堪下泪,谁忍望征尘。
江上风烟积,山幽云雾多。送君南浦外,还望将如何。
桂轺虽不驻,兰筵幸未开。林塘风月赏,还待故人来。
霜华净天末,雾色笼江际。客子常畏人,何为久留滞。
div2的题目确实比较水,进了div1就不同了,除了第一题,后面两道基本没有头绪。。。。。。不过,楼哥依然还是那么猛。。。。
光荣的回到div2...汗...
Class 1
» GeForce GTX 280M SLI
» Mobility Radeon HD 4870 X2
» GeForce GTX 260M SLI
» GeForce 9800M GTX SLI
» GeForce GTX 280M
» GeForce 9800M GT SLI
» GeForce 9800M GTS SLI
» Mobility Radeon HD 3870 X2
» GeForce 8800M GTX SLI
» Mobility Radeon HD 3850 X2
» Quadro FX 3700M
» Mobility Radeon HD 4870
» Mobility Radeon HD 4860
» FirePro M7740
» Mobility Radeon HD 4850
» GeForce GTX 260M
» GeForce 9800M GTX
» GeForce 9800M GT
» GeForce 8800M GTX
» Quadro FX 3600M
» GeForce GTS 260M
» GeForce GTS 250M
» GeForce GTS 160M
» GeForce 9800M GTS
» GeForce 9800M GS
» Mobility Radeon HD 4830
» GeForce GTS 150M
Class 2
» GeForce 8800M GTS
» Mobility Radeon HD 4670
» GeForce 9700M GTS
» Quadro FX 2700M
» Mobility Radeon HD 3870
» Mobility Radeon HD 4650
» GeForce Go 7950 GTX SLI
» GeForce Go 7900 GTX SLI
» Mobility Radeon HD 3850
» GeForce GT 240M
» GeForce Go 7950 GTX
» Quadro FX 3500M
» GeForce 8700M GT SLI
» GeForce Go 7800 GTX SLI
» GeForce Go 7900 GS SLI
» GeForce Go 7900 GTX
» Quadro FX 2500M
» GeForce 8600M GT SLI
» GeForce GT 230M
» GeForce 9700M GT
» GeForce GT 130M
» GeForce 9650M GT
» GeForce Go 7900 GS
» GeForce 9650M GS
» Quadro FX 1700M
» Quadro FX 1600M
» GeForce 8700M GT
» Quadro NVS 320M
» Quadro FX 1500M
» GeForce 9600M GT
» GeForce GT 220M
» Quadro FX 770M
» GeForce GT 120M
» GeForce Go 7800 GTX
» Mobility Radeon HD 3670
» Mobility FireGL V5725
» Mobility Radeon HD 2600 XT
» Mobility Radeon X1900
» Mobility Radeon X1800XT
» Mobility Radeon X1800
» GeForce Go 6800 Ultra
» GeForce Go 7800
» GeForce 9600M GS
» GeForce 9500M GS
» Mobility Radeon HD 4570
» Mobility Radeon HD 2700
» Mobility Radeon HD 3650
» Mobility FireGL V5700
» Quadro FX 570M
» GeForce 8600M GT
» Mobility Radeon HD 2600
» GeForce Go 7600 GT
Class 3
» GeForce G 210M
» GeForce 9500M G
» GeForce 8600M GS
» GeForce Go 7700
» GeForce Go 6800
» Quadro FX Go 1400
» Mobility Radeon X800XT
» Mobility Radeon HD 4530
» Mobility Radeon X1700
» Mobility FireGL V5250
» Mobility Radeon X2500
» GeForce Go 7600
» Quadro NVS 300M
» Mobility Radeon X800
» Mobility Radeon X1600
» Mobility FireGL V5200
» Mobility Radeon 9800
» GeForce Go 6600
» Mobility Radeon X1450
» Mobility Radeon X700
» Mobility FireGL V5000
» GeForce G 110M
» Mobility Radeon HD 4330
» GeForce 8400M GT
» Quadro NVS 140M
» GeForce G 105M
» GeForce 9500M GE
» GeForce G 102M
» GeForce 9400M (G)
» Mobility Radeon HD 3470 Hybrid X2
» GeForce 9400M GeForceBoost
» Mobility Radeon HD 3470
» GeForce 9300M G
» GeForce 9300M GS
» Quadro FX 370M
» Quadro NVS 160M
» GeForce 9200M GS
» Mobility Radeon HD 3450
» Mobility Radeon HD 3430
» Mobility Radeon HD 3410
» Radeon HD 4200
» Quadro NVS 150M
» Mobility Radeon HD 2400 XT
» Quadro FX 360M
» Mobility Radeon X1350
» Mobility Radeon X1400
» GeForce 9100M G
» GeForce 8400M GS
» Quadro NVS 135M
» Mobility Radeon HD 2400
» Radeon HD 3200
» Radeon HD 3100
» Graphics Media Accelerator (GMA) 4700MHD
» GeForce 8400M G
» Graphics Media Accelerator (GMA) 4500MHD
» Graphics Media Accelerator (GMA) 4500M
» Quadro NVS 130M
» GeForce 8200M G
» GeForce Go 7400
» Quadro FX 350M
» Quadro NVS 120M
» GeForce Go 7300
» Quadro NVS 110M
» Mobility Radeon X600
» Mobility FireGL V3200
» Mobility FireGL V3100
» Mobility Radeon X2300
» Mobility Radeon HD 2300
» Mobility Radeon 9700
» Mobility FireGL T2e
Class 4
» Mobility Radeon X1300
» GeForce4 4200 Go
» Mobility Radeon 9600
» Mobility FireGL T2
» Mobility Radeon 9550
» GeForce Go 7200
» GeForce Go 6400
» Mobility Radeon X300
» GeForce Go 6250
» GeForce Go 6200
» GeForce FX Go 5700
» Quadro FX Go 1000
» GeForce FX Go 5600 / 5650
Class 5
» Radeon Xpress X1270
» Radeon Xpress X1250
» Radeon Xpress 1250
» Radeon Xpress X1200
» Graphics Media Accelerator (GMA) X3100
» Radeon Xpress 1150
» GeForce 7150M
» GeForce Go 6150
» GeForce Go 6100
» GeForce 7000M
» Mobility Radeon 9200
» GeForce FX Go 5200
» Mobility Radeon 9000
» GeForce 4 488 Go
» GeForce 4 460 Go
» GeForce 4 440 Go
» GeForce 4 420 Go
» Graphics Media Accelerator (GMA) 950
» Mobility Radeon 7500
» Mobility FireGL 7800
» Graphics Media Accelerator (GMA) 900
» Radeon Xpress 200M
» Radeon Xpress 1100
Class 6
» Mobility FireGL 9000
» Mirage 3+ 672MX
» Mirage 3 671MX
» Graphics Media Accelerator (GMA) 500
» GeForce 3 Go
» GeForce 2 Go (200 / 100)
» Mobility Radeon 9100 IGP
» Mobility Radeon 9000 IGP
» Mobility Radeon M7
» Mobility Radeon M6
» Mobility Radeon 7000 IGP
» Chrome9 HC
» Extreme Graphics 2
» Radeon IGP 340M
» S3G UniChrome Pro II
» S3G UniChrome Pro
» Mirage 2 M760
» Mirage M661FX
» S3 Graphics ProSavage8
» Castle Rock
» Mobility 128 M3
» SM502
摘要:白盒测试作为测试人员常用的一种测试方法,越来越受到测试工程师的重视。白盒测试并不是简单的按照代码设计用例,而是需要根据不同的测试需求,结合不同的测试对象,使用适合的方法进行测试。因为对于不同复杂度的代码逻辑,可以衍生出许多种执行路径,只有适当的测试方法,才能帮助我们从代码的迷雾森林中找到正确的方向。本文介绍六种白盒子测试方法:语句覆盖、判定覆盖、条件覆盖、判定条件覆盖、条件组合覆盖、路径覆盖。
白盒测试的概述
由于逻辑错误和不正确假设与一条程序路径被运行的可能性成反比。由于我们经常相信某逻辑路径不可能被执行, 而事实上,它可能在正常的情况下被执行。由于代码中的笔误是随机且无法杜绝的,因此我们要进行白盒测试。
白盒测试又称结构测试,透明盒测试、逻辑驱动测试或基于代码的测试。白盒测试是一种测试用例设计方法,盒子指的是被测试的软件,白盒指的是盒子是可视的,你清楚盒子内部的东西以及里面是如何运作的。
白盒的测试用例需要做到:
·保证一个模块中的所有独立路径至少 被使用一次
·对所有逻辑值均需测试 true 和 false
·在上下边界及可操作范围内运行所有循环
·检查内部数据结构以确保其有效性
白盒测试的目的:通过检查软件内部的逻辑结构,对软件中的逻辑路径进行覆盖测试;在程序不同地方设立检查点,检查程序的状态,以确定实际运行状态与预期状态是否一致。
白盒测试的特点:依据软件设计说明书进行测试、对程序内部细节的严密检验、针对特定条件设计测试用例、对软件的逻辑路径进行覆盖测试。
白盒测试的实施步骤:
1.测试计划阶段:根据需求说明书,制定测试进度。
2.测试设计阶段:依据程序设计说明书,按照一定规范化的方法进行软件结构划分和设计测试用例。
3.测试执行阶段:输入测试用例,得到测试结果。
4.测试总结阶段:对比测试的结果和代码的预期结果,分析错误原因,找到并解决错误。
白盒测试的方法:总体上分为静态方法和动态方法两大类。
静态分析是一种不通过执行程序而进行测试的技术。静态分析的关键功能是检查软件的表示和描述是否一致,没有冲突或者没有歧义。
动态分析的主要特点是当软件系统在模拟的或真实的环境中执行之前、之中和之后 , 对软件系统行为的分析。动态分析包含了程序在受控的环境下使用特定的期望结果进行正式的运行。它显示了一个系统在检查状态下是正确还是不正确。在动态分析技术中,最重要的技术是路径和分支测试。下面要介绍的六种覆盖测试方法属于动态分析方法。
白盒测试的优缺点
1. 优点
·迫使测试人员去仔细思考软件的实现
·可以检测代码中的每条分支和路径
·揭示隐藏在代码中的错误
·对代码的测试比较彻底
·最优化
2. 缺点
·昂贵
·无法检测代码中遗漏的路径和数据敏感性错误
·不验证规格的正确性
六种覆盖方法
首先为了下文的举例描述方便,这里先给出一张程序流程图。(本文以1995年软件设计师考试的一道考试题目为例,图中红色字母代表程序执行路径)。
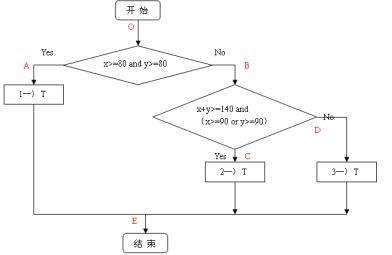
1、语句覆盖
1)主要特点:语句覆盖是最起码的结构覆盖要求,语句覆盖要求设计足够多的测试用例,使得程序中每条语句至少被执行一次。
2)用例设计:(如果此时将A路径上的语句1—〉T去掉,那么用例如下)
|
|
X
|
Y
|
路径
|
|
1
|
50
|
50
|
OBDE
|
|
2
|
90
|
70
|
OBCE
|
3)优点:可以很直观地从源代码得到测试用例,无须细分每条判定表达式。
4)缺点:由于这种测试方法仅仅针对程序逻辑中显式存在的语句,但对于隐藏的条件和可能到达的隐式逻辑分支,是无法测试的。在本例中去掉了语句1—〉T去掉,那么就少了一条测试路径。在if结构中若源代码没有给出else后面的执行分支,那么语句覆盖测试就不会考虑这种情况。但是我们不能排除这种以外的分支不会被执行,而往往这种错误会经常出现。再如,在Do-While结构中,语句覆盖执行其中某一个条件分支。那么显然,语句覆盖对于多分支的逻辑运算是无法全面反映的,它只在乎运行一次,而不考虑其他情况。
2、判定覆盖
1)主要特点:判定覆盖又称为分支覆盖,它要求设计足够多的测试用例,使得程序中每个判定至少有一次为真值,有一次为假值,即:程序中的每个分支至少执行一次。每个判断的取真、取假至少执行一次。
2)用例设计:
|
|
X
|
Y
|
路径
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
3)优点:判定覆盖比语句覆盖要多几乎一倍的测试路径,当然也就具有比语句覆盖更强的测试能力。同样判定覆盖也具有和语句覆盖一样的简单性,无须细分每个判定就可以得到测试用例。
4)缺点:往往大部分的判定语句是由多个逻辑条件组合而成(如,判定语句中包含AND、OR、CASE),若仅仅判断其整个最终结果,而忽略每个条件的取值情况,必然会遗漏部分测试路径。
3、条件覆盖
1)主要特点:条件覆盖要求设计足够多的测试用例,使得判定中的每个条件获得各种可能的结果,即每个条件至少有一次为真值,有一次为假值。
2)用例设计:
|
|
X
|
Y
|
路径
|
|
1
|
90
|
70
|
OBC
|
|
2
|
40
|
|
OBD
|
3)优点:显然条件覆盖比判定覆盖,增加了对符合判定情况的测试,增加了测试路径。
4)缺点:要达到条件覆盖,需要足够多的测试用例,但条件覆盖并不能保证判定覆盖。条件覆盖只能保证每个条件至少有一次为真,而不考虑所有的判定结果。
4、判定/条件覆盖
1)主要特点:设计足够多的测试用例,使得判定中每个条件的所有可能结果至少出现一次,每个判定本身所有可能结果也至少出现一次。
2)用例设计:
|
|
X
|
Y
|
路径
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
|
4
|
70
|
90
|
OBCE
|
3)优点:判定/条件覆盖满足判定覆盖准则和条件覆盖准则,弥补了二者的不足。
4)缺点:判定/条件覆盖准则的缺点是未考虑条件的组合情况。
5、组合覆盖
1)主要特点:要求设计足够多的测试用例,使得每个判定中条件结果的所有可能组合至少出现一次。
2)用例设计:
|
|
X
|
Y
|
路径
|
|
1
|
90
|
90
|
OAE
|
|
2
|
90
|
70
|
OBCE
|
|
3
|
90
|
30
|
OBDE
|
|
4
|
70
|
90
|
OBCE
|
|
5
|
30
|
90
|
OBDE
|
|
6
|
70
|
70
|
OBDE
|
|
7
|
50
|
50
|
OBDE
|
3)优点:多重条件覆盖准则满足判定覆盖、条件覆盖和判定/条件覆盖准则。更改的判定/条件覆盖要求设计足够多的测试用例,使得判定中每个条件的所有可能结果至少出现一次,每个判定本身的所有可能结果也至少出现一次。并且每个条件都显示能单独影响判定结果。
4)缺点:线性地增加了测试用例的数量。
6、路径覆盖
1)主要特点:设计足够的测试用例,覆盖程序中所有可能的路径。
2)用例设计:
|
|
X
|
Y
|
路径
|
|
1
|
90
|
90
|
OAE
|
|
2
|
50
|
50
|
OBDE
|
|
3
|
90
|
70
|
OBCE
|
|
4
|
70
|
90
|
OBCE
|
3)优点:这种测试方法可以对程序进行彻底的测试,比前面五种的覆盖面都广。
4)缺点:由于路径覆盖需要对所有可能的路径进行测试(包括循环、条件组合、分支选择等),那么需要设计大量、复杂的测试用例,使得工作量呈指数级增长。而在有些情况下,一些执行路径是不可能被执行的,如:
If (!A)B++;
If (!A)D--;
这两个语句实际只包括了2条执行路径,即A为真或假时候对B和D的处理,真或假不可能都存在,而路径覆盖测试则认为是包含了真与假的4条执行路径。这样不仅降低了测试效率,而且大量的测试结果的累积,也为排错带来麻烦。
总结
白盒测试是一种被广泛使用的逻辑测试方法,是由程序内部逻辑驱动的一种单元测试方法。只有对程序内部十分了解才能进行适度有效的白盒测试。但是贯穿在程序内部的逻辑存在着不确定性和无穷性,尤其对于大规模复杂软件。因此我们不能穷举所有的逻辑路径,即使穷举也未必会带来好运(穷举不能查出程序逻辑规则错误,不能查出数据相关错误,不能查出程序遗漏的路径)。
那么正确使用白盒测试,就要先从代码分析入手,根据不同的代码逻辑规则、语句执行情况,选用适合的覆盖方法。任何一个高效的测试用例,都是针对具体测试场景的。逻辑测试不是片面的测试正确的结果或是测试错误的结果,而是尽可能全面地覆盖每一个逻辑路径。