The Fourth Dimension Space

枯叶北风寒，忽然年以残，念往昔，语默心酸。二十光阴无一物，韶光贱，寐难安； 不畏形影单，道途阻且慢，哪曲折，如渡飞湍。斩浪劈波酬壮志，同把酒，共言欢！ -如梦令

#

MFC

经过认真的上课听讲以及努力的自学，终于明白MFC是怎么工作的了，呵呵，接下来的目标是做个小游戏，比如扫雷。 呵呵 ，要加油哦！~

posted @ 2009-05-11 23:21 abilitytao 阅读(179) | 评论 (0) | 编辑 收藏

最小堆类

     摘要: #include<iostream>#include<cmath>#include<algorithm>using namespace std;template<class T>class MinHeap{private:    T *heap; &n...  阅读全文

posted @ 2009-05-08 16:57 abilitytao 阅读(405) | 评论 (0) | 编辑 收藏

SortWizard(排序精灵）——我的排序类

     摘要: //排序精灵//Copyright:abilitytao,Nanjing University Of Science And Technology /**//////////////////////////BEGIN_TEMPLATE_BY_ABILITYTAO_ACM///////////////////////////////////...  阅读全文

posted @ 2009-05-07 18:54 abilitytao 阅读(1851) | 评论 (14) | 编辑 收藏

各种排序算法汇总——纪《数据结构》最后一课

     摘要: /**//*<排序算法模板汇总>这些模板适用于任意数据类型，包括结构体和类类型；如果是结构体或者是类类型，请重载"<"符号；PS：这里均按照从小到大的顺序来排序Copyright:abilitytao,Nanjing University Of Science And Technology *//**//////////...  阅读全文

posted @ 2009-05-06 18:13 abilitytao 阅读(1815) | 评论 (4) | 编辑 收藏

简单的哈希查找

//除留余数法实现HASH查找
#include<iostream>
#include<cmath>
using namespace std;

#define HASHSIZE 10000000

struct node
{
    
    int data;
    node *next;
}hashtable[HASHSIZE];

void initial()

{
    
    int i;
    for(i=0;i<HASHSIZE;i++)
    {
        
        hashtable[i].data=-1;
        hashtable[i].next=NULL;
    }
}

void insert(int n)
{
    node *p=&hashtable[n%HASHSIZE];
    node *q=new node;
    q->data=n;
    q->next=p->next;
    p->next=q;
}


node *search(int n)
{
    node *p=hashtable[n%HASHSIZE].next;
    while(p!=NULL)
    {

        if(p->data==n)
            return p;
    }
    return NULL;
}


int main ()
{
    cout<<"请输入数据，并以0结束"<<endl;
    int temp;
    int i;
    for(i=1;;i++)
    {
        cin>>temp;
        if(temp==0)
            break;
        insert(temp);
    }
    cout<<"请输入要查询的数据:";
    cin>>temp;
    node *p=search(temp);
    if(p==NULL)
        cout<<"没有这个数据"<<endl;
    else 
        cout<<p->data<<endl;
    system("pause");
    return 0;
}

posted @ 2009-05-02 16:39 abilitytao 阅读(658) | 评论 (1) | 编辑 收藏

走进MFC的空间

在看了孙鑫的 《C++深入详解》 后，终于能写出个人的第一个MFC程序了，虽然是模仿孙鑫的例程，不过个人非常有成就感呵，希望能早日写出一个功能完整的程序；

#include<windows.h>
#include<stdio.h>
#include<cmath>
#include<iostream>
using namespace std;


LRESULT CALLBACK WinSunProc(
                            HWND hwnd,      // handle to window
                            UINT uMsg,      // message identifier
                            WPARAM wParam,  // first message parameter
                            LPARAM lParam   // second message parameter
                            );

int WINAPI WinMain(
                   HINSTANCE hInstance,      // handle to current instance
                   HINSTANCE hPrevInstance,  // handle to previous instance
                   LPSTR lpCmdLine,          // command line
                   int nCmdShow              // show state
                   )
{
    WNDCLASS wndcls;
    wndcls.cbClsExtra=0;
    wndcls.cbWndExtra=0;
    wndcls.hbrBackground=(HBRUSH)GetStockObject(WHITE_PEN);
    wndcls.hCursor=LoadCursor(NULL,IDC_CROSS);
    wndcls.hIcon=LoadIcon(NULL,IDI_ERROR);
    wndcls.hInstance=hInstance;
    wndcls.lpfnWndProc=WinSunProc;
    wndcls.lpszClassName="abilitytao";
    wndcls.lpszMenuName=NULL;
    wndcls.style=CS_HREDRAW | CS_VREDRAW;
    RegisterClass(&wndcls);
    
    HWND hwnd;
    hwnd=CreateWindow("abilitytao","欢迎来到MFC世界",WS_OVERLAPPEDWINDOW,
        0,0,600,400,NULL,NULL,hInstance,NULL);
    
    ShowWindow(hwnd,SW_SHOWNORMAL);
    UpdateWindow(hwnd);
    
    MSG msg;
    while(GetMessage(&msg,NULL,0,0))
    {
        TranslateMessage(&msg);
        DispatchMessage(&msg);
    }
    return msg.wParam;
}

LRESULT CALLBACK WinSunProc(
                            HWND hwnd,      // handle to window
                            UINT uMsg,      // message identifier
                            WPARAM wParam,  // first message parameter
                            LPARAM lParam   // second message parameter
                            )
{
    switch(uMsg)
    {
    case WM_CHAR:
        char szChar[20];
        sprintf(szChar,"char code is %d",wParam);
        MessageBox(hwnd,szChar,"char",0);
        break;
    case WM_LBUTTONDOWN:
        MessageBox(hwnd,"mouse clicked","message",0);
        HDC hdc;
        hdc=GetDC(hwnd);
        //ReleaseDC(hwnd,hdc);
        break;
    case WM_PAINT:
        HDC hDC;
        PAINTSTRUCT ps;
        hDC=BeginPaint(hwnd,&ps);
        TextOut(hDC,260,100,"hello,MFC",strlen("hello,MFC"));
        TextOut(hDC,350,120,"by  -abilitytao",strlen("by  -abilitytao"));
        EndPaint(hwnd,&ps);
        break;
    case WM_CLOSE:
        if(IDYES==MessageBox(hwnd,"真的要退出吗？","提示",MB_YESNO))
        {
            DestroyWindow(hwnd);
        }
        break;
    case WM_DESTROY:
        PostQuitMessage(0);
        break;
    default:
        return DefWindowProc(hwnd,uMsg,wParam,lParam);
    }
    return 0;
}



感谢那些在我学习过程中给我指点和建议的人！

posted @ 2009-04-29 23:30 abilitytao 阅读(3060) | 评论 (31) | 编辑 收藏

自学MFC

最近选了一门MFC的选修课，本以为MFC应该不难（毕竟C++和各种算法已经研究得很详细了），可是听了几节课下来，感觉自己好像还是没有很大的提高，呵呵，究竟MFC该如何快速入门呢？希望各位牛人能够指点一二，只要让我掌握门道知道怎样自学就行了，不胜感激呵&

posted @ 2009-04-24 00:37 abilitytao 阅读(503) | 评论 (4) | 编辑 收藏

ACM/ICPC 2009 World Final Result

昨天是ACM世界总决赛的日子，所以我特别关注了一下，特别是楼教主呵，听说他是为了拿世界总决赛冠军才复出的，不过最后的结果很遗憾
啊，上届冠军SPSU以罚时优势成功卫冕，让清华再次饮憾屈居亚军。

冠军：St. Petersburg State University of IT, Mechanics and Optics 俄罗斯

亚军：Tsinghua University 中国

季军：St. Petersburg State University 俄罗斯

 

ZSU最终5题排名20，本次中国总共有15支队在3题以上。

 

详细的排名如下：

----------------------------------------------------------------------------------

Place

 Name Solved Time
1 St. Petersburg State University of IT, Mechanics and Optics 9 1381
2 Tsinghua University 9 1800
3 St. Petersburg State University 8 1176
4 Saratov State University 8 1305
5 University of Oxford 7 998
6 Zhejiang University 7 1117
7 Massachusetts Institute of Technology 7 1143
8 Altai State Technical University 7 1254
9 University of Warsaw 7 1413
10 University of Waterloo 6 787
11 I. Javakhishvili Tbilisi State University 6 933
12 Carnegie Mellon University 6 1045
13 South China University of Technology 6 1058
14 Sharif University of Technology 6  
14 Seoul National University 6  
14 Fudan University 6  
14 Moscow State University 6  
14 National Taiwan University 6  
14 Shanghai Jiaotong University 6  
20 Stanford University 5  
20 Novosibirsk State University 5  
20 Ural State University 5  
20 University of Maryland 5  
20 Universidad de Buenos Aires - FCEN 5  
20 University of Cambridge - Trinity College 5  
20 University of Tokyo 5  
20 Peking University 5  
20 University of Melbourne 5  
20 Huazhong University of Science & Technology 5  
20 Zhejiang University of Technology 5  
20 Zhongshan (Sun Yat-sen) University 5  
20 Taurida V.I. Vernadsky National University 5  
20 Chinese University of Hong Kong 5  
34 University of British Columbia 4  
34 Bangladesh University of Engineering and Technology 4  
34 National Technical University of Ukraine "KPI" 4  
34 Belarusian State University 4  
34 Taras Shevchenko Kiev National University 4  
34 University of California at Berkeley 4  
34 Tianjin University 4  
34 Universidade Federal do Paraná 4  
34 Amirkabir University of Technology 4  
34 Sichuan University 4  
34 Jagiellonian University in Krakow 4  
34 KTH - Royal Institute of Technology 4  
34 Beijing Jiaotong University 4  
34 École Normale Supérieure de Lyon 4  
34 Beijing University of Posts and Telecommunications 4  
49 Nanjing University 3  
49 Universitat Politècnica de Catalunya 3  
49 Instituto Tecnológico de Culiacán 3  
49 German University in Cairo 3  
49 University of Cape Town 3  
49 South Ural State University 3  
49 University of Aizu 3  
49 Nanyang Technological University 3  
49 Universidad Nacional de Colombia - Bogotá 3  
49 University of Canterbury 3  
49 Korea Advanced Institute of Science and Technology 3  
49 Universidad Nacional del Sur 3  
49 Iowa State University 3  
49 Cornell University 3  
49 University of Tasmania 3  
49 University of Texas at Austin 3  
49 University of Wisconsin - Madison 3  
49 University of Dhaka 3  
49 University of Illinois - Urbana-Champaign 3  

posted @ 2009-04-22 18:22 abilitytao 阅读(3360) | 评论 (9) | 编辑 收藏

Floyd-Warshall算法详解（转）

Floyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。我们平时所见的Floyd算法的一般形式如下：
1 void Floyd(){
2     int i,j,k;
3     for(k=1;k<=n;k++)
4         for(i=1;i<=n;i++)
5             for(j=1;j<=n;j++)
6                 if(dist[i][k]+dist[k][j]<dist[i][j])
7                     dist[i][j]=dist[i][k]+dist[k][j];
8 }

  注意下第6行这个地方，如果dist[i][k]或者dist[k][j]不存在，程序中用一个很大的数代替。最好写成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j])，从而防止溢出所造成的错误。
  上面这个形式的算法其实是Floyd算法的精简版，而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。
  设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度，其中k 表示该路径中的最大顶点，也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此，如果G中包含边<i, j>，则c[i, j, 0] =边<i, j> 的长度；若i= j ，则c[i,j,0]=0；如果G中不包含边<i, j>，则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。
  对于任意的k>0，通过分析可以得到：中间顶点不超过k 的i 到j 的最短路径有两种可能：该路径含或不含中间顶点k。若不含，则该路径长度应为c[i, j, k-1]，否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。
  状态转移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。
  这样，问题便具有了最优子结构性质，可以用动态规划方法来求解。

  为了进一步理解，观察上面这个有向图：若k=0, 1, 2, 3，则c[1,3,k]= +∞；c[1,3,4]= 28；若k = 5, 6, 7，则c [1,3,k] = 10；若k=8, 9, 10，则c[1,3,k] = 9。因此1到3的最短路径长度为9。
  下面通过程序来分析这一DP过程，对应上面给出的有向图：

 

 1 #include <iostream>
 2 using namespace std;
 3 
 4 const int INF = 100000;
 5 int n=10,map[11][11],dist[11][11][11];
 6 void init(){
 7     int i,j;
 8     for(i=1;i<=n;i++)
 9         for(j=1;j<=n;j++)
10             map[i][j]=(i==j)?0:INF;
11     map[1][2]=2,map[1][4]=20,map[2][5]=1;
12     map[3][1]=3,map[4][3]=8,map[4][6]=6;
13     map[4][7]=4,map[5][3]=7,map[5][8]=3;
14     map[6][3]=1,map[7][8]=1,map[8][6]=2;
15     map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
17 void floyd_dp(){
18     int i,j,k;
19     for(i=1;i<=n;i++)
20         for(j=1;j<=n;j++)
21             dist[i][j][0]=map[i][j];
22     for(k=1;k<=n;k++)
23         for(i=1;i<=n;i++)
24             for(j=1;j<=n;j++){
25                 dist[i][j][k]=dist[i][j][k-1];
26                 if(dist[i][k][k-1]+dist[k][j][k-1]<dist[i][j][k])
27                     dist[i][j][k]=dist[i][k][k-1]+dist[k][j][k-1];
28             }
29 }
30 int main(){
31     int k,u,v;
32     init();
33     floyd_dp();
34     while(cin>>u>>v,u||v){
35         for(k=0;k<=n;k++){
36             if(dist[u][v][k]==INF) cout<<"+∞"<<endl;
37             else cout<<dist[u][v][k]<<endl;
38         }
39     }
40     return 0;
41 }

  输入 1 3
  输出 +∞
            +∞
            +∞
            +∞
            28
            10
            10
            10
            9
            9
            9

  Floyd-Warshall算法不仅能求出任意2点间的最短路径，还可以保存最短路径上经过的节点。下面用精简版的Floyd算法实现这一过程，程序中的图依然对应上面的有向图。

 1 #include <iostream>
 2 using namespace std;
 3 
 4 const int INF = 100000;
 5 int n=10,path[11][11],dist[11][11],map[11][11];
 6 void init(){
 7     int i,j;
 8     for(i=1;i<=n;i++)
 9         for(j=1;j<=n;j++)
10             map[i][j]=(i==j)?0:INF;
11     map[1][2]=2,map[1][4]=20,map[2][5]=1;
12     map[3][1]=3,map[4][3]=8,map[4][6]=6;
13     map[4][7]=4,map[5][3]=7,map[5][8]=3;
14     map[6][3]=1,map[7][8]=1,map[8][6]=2;
15     map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
17 void floyd(){
18     int i,j,k;
19     for(i=1;i<=n;i++)
20         for(j=1;j<=n;j++)
21             dist[i][j]=map[i][j],path[i][j]=0;
22     for(k=1;k<=n;k++)
23         for(i=1;i<=n;i++)
24             for(j=1;j<=n;j++)
25                 if(dist[i][k]+dist[k][j]<dist[i][j])
26                     dist[i][j]=dist[i][k]+dist[k][j],path[i][j]=k;
27 }
28 void output(int i,int j){
29     if(i==j) return;
30     if(path[i][j]==0) cout<<j<<' ';
31     else{
32         output(i,path[i][j]);
33         output(path[i][j],j);
34     }
35 }
36 int main(){
37     int u,v;
38     init();
39     floyd();
40     while(cin>>u>>v,u||v){
41         if(dist[u][v]==INF) cout<<"No path"<<endl;
42         else{
43             cout<<u<<' ';
44             output(u,v);
45             cout<<endl;
46         }
47     }
48     return 0;
49 }

  输入 1 3                    
  输出 1 2 5 8 6 3


转自：http://www.cppblog.com/mythit/archive/2009/04/21/80579.html

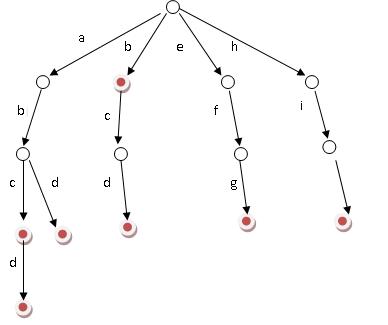
posted @ 2009-04-22 16:52 abilitytao 阅读(2141) | 评论 (0) | 编辑 收藏

Trie树|字典树的简介及实现（转）

Trie,又称字典树、单词查找树,是一种树形结构，用于保存大量的字符串。它的优点是：利用字符串的公共前缀来节约存储空间。
相对来说,Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.当然,或许用左儿子右兄弟的方法建树的话,可能会好点.

其基本性质可以归纳为：
1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

其基本操作有:查找 插入和删除,当然删除操作比较少见.我在这里只是实现了对整个树的删除操作,至于单个word的删除操作也很简单.

搜索字典项目的方法为：

(1) 从根结点开始一次搜索；

(2) 取得要查找关键词的第一个字母，并根据该字母选择对应的子树并转到该子树继续进行检索；

(3) 在相应的子树上，取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处，关键词的所有字母已被取出，则读取附在该结点上的信息，即完成查找。
其他操作类似处理.

 

/*
Name: Trie树的基本实现 
Author: MaiK 
Description: Trie树的基本实现 ,包括查找 插入和删除操作*/
#include<algorithm>
#include<iostream>
using namespace std;

const int sonnum=26,base='a';
struct Trie
{
    int num;//to remember how many word can reach here,that is to say,prefix
    bool terminal;//If terminal==true ,the current point has no following point
    struct Trie *son[sonnum];//the following point
};
Trie *NewTrie()// create a new node
{
    Trie *temp=new Trie;
    temp->num=1;temp->terminal=false;
    for(int i=0;i<sonnum;++i)temp->son[i]=NULL;
    return temp;
}
void Insert(Trie *pnt,char *s,int len)// insert a new word to Trie tree
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
    {
        if(temp->son[s[i]-base]==NULL)temp->son[s[i]-base]=NewTrie();
        else temp->son[s[i]-base]->num++;
        temp=temp->son[s[i]-base];
    }
    temp->terminal=true;
}
void Delete(Trie *pnt)// delete the whole tree
{
    if(pnt!=NULL)
    {
        for(int i=0;i<sonnum;++i)if(pnt->son[i]!=NULL)Delete(pnt->son[i]);
        delete pnt; 
        pnt=NULL;
    }
}
Trie* Find(Trie *pnt,char *s,int len)//trie to find the current word
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
        if(temp->son[s[i]-base]!=NULL)temp=temp->son[s[i]-base];
        else return NULL;
    return temp;
} 


转自：http://hi.baidu.com/luyade1987/blog/item/2667811631106657f2de320a.html

posted @ 2009-04-21 12:08 abilitytao 阅读(26731) | 评论 (12) | 编辑 收藏

仅列出标题
共42页: First 30 31 32 33 34 35 36 37 38 Last