#
经过前面的章节，我们已经能够画出一些东西来，主要就是使用QPainter的相关函数。今天，我们要看的是QPainter的坐标系统。
同很多坐标系统一样，QPainter的默认坐标的原点(0, 0)位于屏幕的左上角，X轴正方向是水平向右，Y轴正方向是竖直向下。在这个坐标系统中，每个像素占据1 x 1的空间。你可以把它想象成是一张坐标值，其中的每个小格都是1个像素。这么说来，一个像素的中心实际上是一个“半像素坐标系”，也就是说，像素(x, y)的中心位置其实是在(x + 0.5, y + 0.5)的位置上。因此，如果我们使用QPainter在(100, 100)处绘制一个像素，那么，这个像素的中心坐标是(100.5, 100.5)。
这种细微的差别在实际应用中，特别是对坐标要求精确的系统中是很重要的。首先，只有在禁止反走样，也就是默认状态下，才会有这0.5像素的偏移；如果使用了反走样，那么，我们画(100, 100)位置的像素时，QPainter会在(99.5, 99.5)，(99.5, 100.5)，(100.5, 99.5)和(100.5, 100.5)四个位置绘制一个亮色的像素，这么产生的效果就是在这四个像素的焦点处(100, 100)产生了一个像素。如果不需要这个特性，就需要将QPainter的坐标系平移(0.5, 0.5)。
这一特性在绘制直线、矩形等图形的时候都会用到。下图给出了在没有反走样技术时，使用drawRect(2, 2, 6, 5)绘制一个矩形的示例。在No Pen的情况下，请注意矩形左上角的像素是在(2, 2)，其中心位置是在(2.5, 2.5)的位置。然后注意下有不同的Pen的值的绘制样式，在Pen宽为1时，实际画出的矩形的面积是7 x 6的(图出自C++ GUI Programming with Qt4, 2nd Edition)：
在具有反走样时，使用drawRect(2, 2, 6, 5)的效果如下(图出自C++ GUI Programming with Qt4, 2nd Edition)：
注意我们前面说过，通过平移QPainter的坐标系来消除着0.5像素的差异。下面给出了使用drawRect(2.5, 2.5, 6, 5)在反走样情况下绘制的矩形(图出自C++ GUI Programming with Qt4, 2nd Edition)：
请对比与上图的区别。
在上述的QPainter的默认坐标系下，QPainter提供了视口(viewport)窗口(window)机制，用于绘制与绘制设备的大小和分辨率无关的图形。视口和窗口是紧密的联系在一起的，它们一般都是矩形。视口是由物理坐标确定其大小，而窗口则是由逻辑坐标决定。我们在使用QPainter进行绘制时，传给QPainter的是逻辑坐标，然后，Qt的绘图机制会使用坐标变换将逻辑坐标转换成物理坐标后进行绘制。
通常，视口和窗口的坐标是一致的。比如一个600 x 800的widget(这是一个widget，或许是一个对话框，或许是一个面板等等)，默认情况下，视口和窗口都是一个320 x 200的矩形，原点都在(0, 0)，此时，视口和窗口的坐标是相同的。
注意到QPainter提供了setWindow()和setViewport()函数，用来设置视口和窗口的矩形大小。比如，在上面所述的320 x 200的widget中，我们要设置一个从(-50, -50)到(+50, +50)，原点在中心的矩形窗口，就可以使用
painter.setWindow(-50, -50, 100, 100);
其中，(-50, -50)指明了原点，100, 100指明了窗口的长和宽。这里的“指明原点”意思是，逻辑坐标的(-50, -50)对应着物理坐标的(0, 0)；“长和宽”说明，逻辑坐标系下的长100，宽100实际上对应物理坐标系的长320，宽200。
或许你已经发现这么一个好处，我们可以随时改变window的范围，而不改变底层物理坐标系。这就是前面所说的，视口与窗口的作用：“绘制与绘制设备的大小和分辨率无关的图形”，如下图所示(图出自C++ GUI Programming with Qt4, 2nd Edition)：
除了视口与窗口的变化，QPainter还提供了一个“世界坐标系”，同样也可以变换图形。所不同的是，视口与窗口实际上是统一图形在两个坐标系下的表达，而世界坐标系的变换是通过改变坐标系来平移、缩放、旋转、剪切图形。为了清楚起见，我们来看下面一个例子：
void PaintedWidget::paintEvent(QPaintEvent *
event)
{
QPainter painter(
this);
QFont font(
"Courier", 24);
painter.setFont(font);
painter.drawText(50, 50,
"Hello, world!");
QTransform transform;
transform.rotate(+45.0);
painter.setWorldTransform(transform);
painter.drawText(60, 60,
"Hello, world!");
}
为了显示方便，我在这里使用了QFont改变了字体。QPainter的drawText()函数提供了绘制文本的功能。它有几种重载形式，我们使用了其中的一种，即制定文本的坐标然后绘制。需要注意的是，这里的坐标是文字左下角的坐标(特别提醒这一点，因为很多绘图系统，比如Java2D都是把左上角作为坐标点的)！下面是运行结果：
我们使用QTransform做了一个rotate变换。这个变换就是旋转，而且是顺时针旋转45度。然后我们使用这个变换设置了QPainter的世界坐标系，注意到QPainter是一个状态机，所以这种变换并不会改变之前的状态，因此只有第二个Hello, world!被旋转了。确切的说，被旋转的是坐标系而不是这个文字！请注意体会这两种说法的不同。
本文出自 “豆子空间” 博客，请务必保留此出处http://devbean.blog.51cto.com/448512/239585
虽然按照网上的教程安装并编译了QT4.7，但是安装过QT插件之后还是无法正常配置。
在option配置路径的时候，2010显示
QT in the given path was built using minGW
一个莫名其妙的错误，都来查询了一些国外的论坛发现，这是插件的一个bug...我勒个去..
解决方法如下：
1.修改注册表:
HKEY_CURRENT_USER\Software\Trolltech\Versions\
下增加一个子项
qt201005（需要的名称）
子项下面增加一个数值 InstallDir，值就是你要配置的Qt路径
2.删除文件
删除lib目录下的
libqtmain.a and libqtmaind.a 两个文件。
运行第一个示例程序如下：
使用QT建了个简单的项目，发现无法通过编译，崩溃。。。后来发现路径名中不能用中文！
开发环境总算是搭建完成。
在编译QT代码时，会遇到一些问题，我遇到了两个问题。
然后继续编译N久之后，又出现了问题。。。
编译大概1个小时之后，出现：
01.api\qscriptextensionplugin.h(43): Error: Undefined interface
02.NMAKE : fatal error U1077: 'C:\Qt\2009.05\qt\bin\moc.exe' : return code '0x1'
03.Stop.
04.NMAKE : fatal error U1077: '"d:\Program Files\Microsoft Visual Studio 9.0\VC\BIN
05.\nmake.exe"' : return code '0x2'
06.Stop.
07.NMAKE : fatal error U1077: 'cd' : return code '0x2'
08.Stop.
api\qscriptextensionplugin.h(43): Error: Undefined interface
NMAKE : fatal error U1077: 'C:\Qt\2009.05\qt\bin\moc.exe' : return code '0x1'
Stop.
NMAKE : fatal error U1077: '"d:\Program Files\Microsoft Visual Studio 9.0\VC\BIN
\nmake.exe"' : return code '0x2'
Stop.
NMAKE : fatal error U1077: 'cd' : return code '0x2'
Stop.
以上是出错代码，解决方法是将
qt/src/script/tmp/moc/debug_shared/mocinclude.tmp
qt/src/script/tmp/moc/release_shared/mocinclude.tmp
删除，然后继续编译。
过了很长时间之后，在编译webkit部分的代码时，会发生错误，系统会停止编译
D:\tools\Qt\2010.05\qt\src\3rdparty\webkit\WebCore\tmp\moc\debug_shared\moc_Sock
etStreamHandlePrivate.cpp(97) : error C2065: “QSslError”: 未声明的标识符
D:\tools\Qt\2010.05\qt\src\3rdparty\webkit\WebCore\tmp\moc\debug_shared\moc_Sock
etStreamHandlePrivate.cpp(97) : error C3861: “socketSslErrors”: 找不到标识符
正在生成代码...
NMAKE : fatal error U1077: “"D:\tools\Microsoft Visual Studio 10.0\VC\BIN\cl.EX
E"”: 返回代码“0x2”
Stop.
NMAKE : fatal error U1077: “"D:\tools\Microsoft Visual Studio 10.0\VC\BIN\nmake
.exe"”: 返回代码“0x2”
Stop.
NMAKE : fatal error U1077: “cd”: 返回代码“0x2”
Stop.
解决方法是将
qt\src\3rdparty\webkit\WebCore\tmp\moc\debug_shared\mocinclude.tmp
qt\src\3rdparty\webkit\WebCore\tmp\moc\release_shared\mocinclude.tmp
删除之后可以继续编译(重新执行nmake命令)
Qt – 一个跨平台应用程序和UI开发框架
它包括跨平台类库、集成开发工具和跨平台 IDE。使用 Qt 您只需一次性开发应用程序，无须重新编写源代码，便可跨不同桌面和嵌入式操作系统部署这些应用程序。
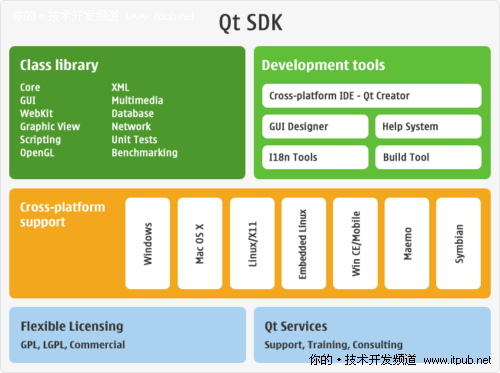
Qt 主要是由 诺基亚 开发和维护的。Qt通过开源授权(LGPL 和 GPL)以及商业授权的方式对 Qt 进行授权。在Linux下Qt可是大名鼎鼎，Linux的KDE图形界面就是基于Qt开发的。
Qt的最大好处是跨平台，可以看到上图，Qt可以支持windows，Mac os，linux，embedded linux， wince/mobile，symbian，诺基亚最新的Megoo那也是不在话下了，由于公司最近有些项目要求跨平台的支持，原来的GIS引擎是基于Windows开发的，虽然没有用MFC，但是由于绘图引擎这块使用的GDI+，所以跨平台是非常困难的。所以为了支持跨平台以及在可预见的将来的跨平台的需求，决定将绘图引擎这块在Qt的基础上进行重构，并使用Qt开发一套基于QtGis引擎的地图项目管理应用程序。
我在博客中将会同步将开发这个应用程序的步骤展示出来，希望能通过这个系列的博客，来展示Qt开发应用程序的便利性以及展示我们公司GIS引擎的强大能力。应用程序的源代码将会同步放在每篇教程内提供下载。Gis引擎将通过提供SDK的方式方便大家学习及开发。
第一篇. 配置Qt的windows开发环境,并通过Visual Studio 2010进行开发。
1. 下载Qt的安装包和Visual Studio 2010的Qt插件，大家可以到下面的地址进行下载(下面的下载都是基于Windows的，如果是其他环境的操作系统可以到这里下载).
Qt SDK: http://qt.nokia.com/downloads/sdk-windows-cpp
Visual Studio 2010开发插件: http://qt.nokia.com/downloads/visual-studio-add-in
2. 安装Qt SDK
安装其实很简单了，基本上一路回车即可，主要是要注意下Qt的安装路径最好安装在全英文路径而且中间没有空格, 安装好后，可以运行开始菜单里面的Qt Demo，直观感受下Qt的强大功能!
界面非常炫酷
3. 安装Qt的VS开发插件
同安装Qt SDK一样，一路上回车即可，安装后在Visual Studio 2010上新增一菜单Qt，如图所示
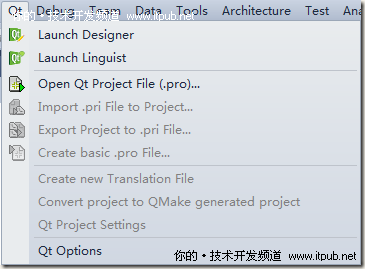
4. 编译Qt
Qt默认使用mingw进行编译，如果要使用Visual Studio 2010开发，需要将Qt重新编译。
进入开始菜单Microsoft Visual Studio 2010，Visual Studio Tools，Visual Studio Command Prompt (2010)，需要注意的是，这里面必须是使用Visual Studio Command Prompt (2010)，不能使用CMD的Dos窗口
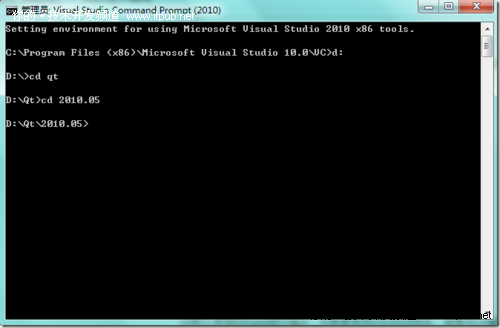
进入Qt的安装目录后，执行CD Qt，进入Qt的根目录
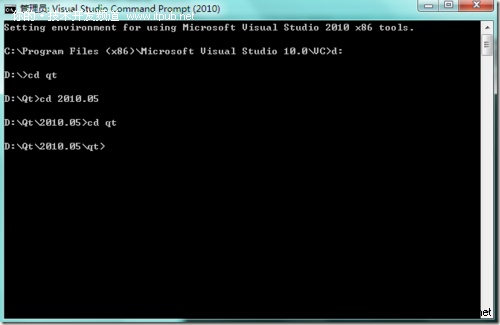
运行命令 configure -platform win32-msvc2010，o(选择opensource模式)回车,Y(同意license)回车
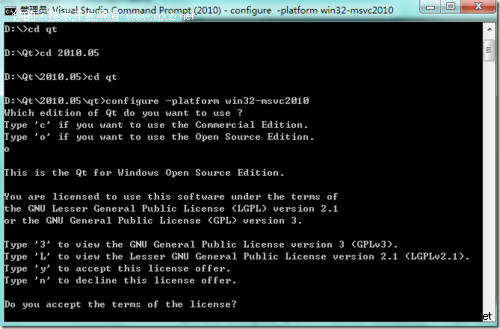
接着就会自动配置Qt的编译环境，等配置结束后,运行nmake,回车，Qt就会开始漫长的编译过程，这段时间非常长，需要4个小时以上，大家可以在晚上睡觉的时候进行编译。
5.配置Visual Studio 2010的Qt开发环境(Visual Studio 2010最好是英文版本，Qt对Visual Studio 2010中文版本可能支持的不好)
等Qt编译好后就可以配置Visual Studio 2010的开发环境了，进入Visual Studio 2010，选择Qt菜单，Qt Option，进入下图界面
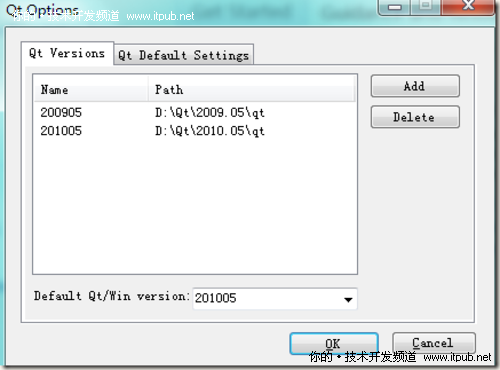
点击Add，添加Qt的安装目录，并取名字，我这里使用Qt的发现版本最为名称，选择OK后即可。
6.新建或者导入Qt项目
可以通过在Visual Studio 2010新建一个Qt项目
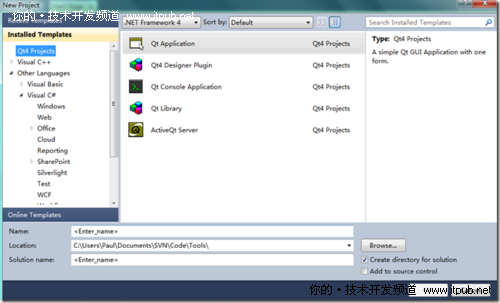
导入Qt的Pro项目Pro是Qt自带编译器Qt Creator的项目工程文件，如果想使用Visual Studio 2010开发则需要将原有项目的Pro导入到Visual Studio 2010的项目文件中，可以使用菜单Qt-Open
这样我们的Qt开发环境就搭建好了，大家可以将Qt目录下的Example和Demo下的例子的运行看一遍，体验下Qt的强大和便捷，Enjoy!
文章转自:http://tech.it168.com/a2010/1217/1139/000001139431.shtml
Qt 深入浅出
经常有人问哪里有学习Qt的资料，Qt的教程，怎么才能入门等等，或者抱怨说中文的信息太少。其实网上有很多关于Qt的学习资料，今天在这里总结一下，希望各位想学习Qt的同学，各取所需，早日从入门到精通！
Part 1: 新手上路
Qt 官方学习教程
Qt 官方学习教程包含了3部分，包括如何学习Qt，如何逐步创建一个地址簿应用以及如何编写Qt Widget。教程由浅入深，Qt初学者必读
我们假定您已了解 C++， 并将用于 Qt 开发。有关将 Qt 与其他编程语言一起使用的更多信息，请参见 Qt 网站。。。。。
本教程介绍了使用 Qt 跨平台框架的 GUI 编程。在学习过程中，我们将了解部分 Qt 基本技术，如Widget 和布局管理器，容器类，信号和槽，输入和输出设备等。。
Widget 是使用 Qt 编写的图形用户界面 (GUI) 应用程序的基本生成块。每个 GUI 组件，如按钮、标签或文本编辑器，都是一个 widget ，并可以放置在现有的用户界面中或作为单独的窗口显示。每种类型的组件都是由 QWidget 的特殊子类提供的，而 QWidget 自身又是 QObject 的子类。
Qt 学习之路:
来自于FinderCheng的Qt 学习之路。简介：在本系列文章中，FinderCheng使用Qt4进行C++ GUI的开发。我是参照着《C++ GUI Programming with Qt4》一书进行学习的。其实，我也只是初学Qt4，在这里将这个学习笔记记下来，希望能够方便更多的朋友学习Qt4。我是一个Java程序员，感觉 Qt4的一些命名规范以及约束同Java有异曲同工之妙，因而从Java迁移到Qt4似乎困难不大。不过，这也主要是因为Qt4良好的设计等等。
Qt是一个著名的C++库——或许并不能说这只是一个GUI库，因为Qt十分庞大，并不仅仅是GUI。使用Qt，在一定程序上你获得的是一个“一站式”的服务：不再需要研究STL，不再需要C++的 ，因为Qt有它自己的QString等等。或许这样说很偏激，但Qt确实是一个 “伟大的C++库”。
任何编程技术的学习第一课基本上都会是Hello, world!，我也不想故意打破这个惯例——照理说，应该首先回顾一下Qt的历史，不过即使不说这些也并无大碍。
下面来逐行解释一下前面的那个Hello, world!程序，尽管很简单，但却可以对Qt程序的结构有一个清楚的认识。现在再把代码贴过来：
所谓信号槽，简单来说，就像是插销一样：一个插头和一个插座。怎么说呢？当某种事件发生之后，比如，点击了一下鼠标，或者按了某个按键，这时，这个组件就 会发出一个信号。就像是广播一样，如果有了事件，它就漫天发声。这时，如果有一个槽，正好对应上这个信号，那么，这个槽的函数就会执行，也就是回调。就像 广播发出了，如果你感兴趣，那么你就会对这个广播有反应。干巴巴的解释很无力，还是看代码：
顾名思义，绝对定位就是使用最原始的定位方法，给出这个组件的坐标和长宽值。这样，Qt就知道该把组件放在哪里，以及怎么设置组件的大小了。但是这样做的 一个问题是，如果用户改变了窗口大小，比如点击了最大化或者拖动窗口边缘，这时，你就要自己编写相应的函数来响应这些变化，以避免那些组件还只是静静地呆 在一个角落。或者，更简单的方法是直接禁止用户改变大小。
今天来说一下有关Qt API文档的使用。因为Qt有一个商业版本，因此它的文档十分健全，而且编写良好。对于开发者来说，查看文档时开发必修课之一——没有人能够记住那么多API的使用！
首先说明一点，在C++ GUI Programming with Qt4, 2nd中，这一章连同以后的若干章一起，完成了一个比较完整的程序——一个模仿Excel的电子表格。不过这个程序挺大的，而且书中也没有给出完整的源代 码，只是分段分段的——我不喜欢这个样子，我想要看到我写出来的是什么东西，这是最主要的，而不是慢慢的过上几章的内容才能看到自己的作品。
Qt是分模块的，记得我们建工程的时候就会问你，使用哪些模块？QtCore？QtGui？QtXml？等等。这里，我们引入QtGui，它包括了 QtCore和QtGui模块。不过，这并不是最好的做法，因为QtGui文件很大，包括了GUI的所有组件，但是很多组件我们根本是用不到的——就像 Swing的import，
槽函数和 普通的C++成员函数没有很大的区别。它们也可以使virtual的；可以被重写；可以使public、protected或者private 的；可以由其它的C++函数调用；参数可以是任何类型的。如果要说区别，就是，槽函数可以和一个信号相连接，当这个信号发生时，它可以被自动调用。
前面说过，Qt使用的是自己的预编译器，它提供了对C++的一种扩展。利用Qt的信号槽机制，就可以把彼此独立的模块相互连接起来，不需要实现知道模块的任何细节。为了达到这个目的，Qt提出了一个Meta-Object系统。它提供了两个关键的作用：信号槽和内省。
尽管Qt提供了很方便的快速开发工具QtDesigner用来拖放界面元素，但是现在我并不打算去介绍这个工具，原因之一在于我们的学习大体上是依靠手工编写代码，过早的接触设计工具并不能让我们对Qt的概念突飞猛进
在前面的QMainWindow的基础之上，我们开始着手建造我们的应用程序。虽然现在已经有一个框架，但是，确切地说我们还一行代码没有写呢！下面的工作就不那么简单了！在这一节里面，我们要为我们的框架添加菜单和工具条。
前面一节我们已经把QAction添加到菜单和工具条上面。现在我们要添加一些图片美化一下，然后把信号槽加上，这样，我们的action就可以相应啦！
今天的内容主要还是继续完善前面的那个程序。我们要为我们的程序加上一个状态栏。
下面还是按照我们的进度，从Qt的标准对话框开始说起。所谓标准对话框，其实就是Qt内置的一些对话框，比如文件选择、颜色选择等等。今天首先介绍一下QFileDialog。
继续来说Qt的标准对话框，这次说说QColorDialog。这是Qt提供的颜色选择对话框。
程序写的多了，你会发现几乎所有的Qt类的构造函数都会有一个parent参数。这个参数通常是QObject* 或者是 QWidget* 类型的。
这次来说一下QMessageBox以及类似的几种对话框。其实，我们已经用过QMessageBox了，就在之前的几个程序中。
这是Qt标准对话框的最后一部分。正如同其名字显示的一样，QInputDialog用于接收用户的输入。
Part 2： 进阶学习
Qt4 学习笔记
来自台湾的caterpillar，Qt4 学习笔记由浅入深，分门别类的介绍了Qt4 中的许多特性，如事件處理，常用圖型元件，常用 API，檔案處理，拖放（Drag & Drop）與剪貼，多執行緒（Multithreading）很多内容，是进一步学习Qt的极好教程
Qt 开发实例
这里我们将会构建所能想到的最简单和最直观的音乐播放器，给用户提供另一个选择。 从苹果的新款iPod Shuffle吸取一些灵感，只提供最基本的控制功能。
如果说有一种工具非常需要GUI，那就是FFMPEG。FFMPEG是一个十分优秀的命令行应用程序，它可以将视频和电影文件从一种格式转换为另一种格式。
这个应用程序就是一个RSS阅读器，它允许用户添加自己的种子，列出该种子上的内容，然后让用户在主应用程序自带的一个浏览器窗口中阅读这些内容。
Qt Graphics View详解
来自清源游民的Qt笔记，详解介绍了Qt Graphics View中各个对象的概念和使用方法。对于Graphics View的学习大有裨益。
Graphics View提供了一个界面，它既可以管理大数量的定制2D graphical items，又可与它们交互，有一个view widget可以把这些项绘制出来，并支持旋转与缩放。
Graphics View基于笛卡尔坐标系。item在场景中的位置与几何形状通过x,y坐标表示。当使用未经变形的视图来观察场景时，场景中的一个单位等于屏幕上的一个像素。
QGraphicsView通过QGraphicsView::setMatrix()支持同QPainter一样的仿射变换，通过对一个视图应用变换，你可以很容易地支持普通的导航特性如缩放与旋转。
关于Qt编程的书籍
接下来当你学习了上面的相关内容后，就可以开始阅读Qt编程的书籍进行系统的学习了。当然，书也不一定要从头到尾阅读一遍，用时拿出来学习和参考也很不错
本书详细讲述了用最新的Qt版本进行图形用户界面应用程序开发的各个方面。前5章主要涉及Qt基础知识，后两个部分主要讲解Qt的中高级编程，包括布局管 理、事件处理、二维/三维图形、拖放、项视图类、容器类、输入/输出、数据库、多线程、网络、XML、国际化、嵌入式编程等内容。对于本书讲授的大量 Qt4编程原理和实践，都可以轻易将其应用于Qt4．4、Qt4．5以及后续版本的Qt程序开发过程中。
Part3：深入理解
Inside Qt 系列
QKevin所著，通过剖析Qt源代码，深入浅出的解释了Qt中的许多机制，了解Qt内部是如何 work 的。着实为想深入了解Qt的开发者提供了很好的学习机会。如果你已经学习了上面的内容并且熟练掌握Qt编程，那么大力推荐这一系列文章！
写了这么多年的程序，除了留下很多 code (其中有很多是garbage)之外，再没有其它东西，或许我该写点儿什么了，写一些关于我的工作的东西，自己所了解的技术，也把自己在工作过程中新学习的一些东西放在这儿，就算是为了以后做一个参考。
QObject 这个 class 是 QT 对象模型的核心，绝大部分的 QT 类都是从这个类继承而来。这个模型的中心特征就是一个叫做信号和槽（signal and slot）的机制来实现对象间的通讯，
我们知道，在C++中，几乎每一个类(class)中都需要有一些类的成员变量(class member variable)，在通常情况下的做法如下：
在 QT 4.4 中，类成员变量定义方法的出发点没有变化，只是在具体的实现手段上发生了非常大的变化，下面具体来看。
接上节，让我们来看看这个 QObjectPrivate 和 QObject 是如何关联在一起的。
从本节开始，我们讲解 QT Meta-Object System 的功能，以及实现。在使用 Qt 开发的过程中，大量的使用了 signal 和 slot. 比如，响应一个 button 的 click 事件，我们一般都写如下的代码：
元对象编译器用来处理QT 的C++扩展，moc 分析C＋＋源文件，如果它发现在一个头文件(header file)中包含Q_OBJECT 宏定义，然后动态的生成另外一个C++源文件
信号和 槽是用来在对象间通讯的方法，当一个特定事件发生的时候，signal会被 emit 出来，slot 调用是用来响应相应的 signal 的。
前面我们介绍了 Meta Object 的基本功能，和它支持的最重要的特性之一：Signal & Slot的基本功能。现在让我们来进入 Meta Object 的内部，看看它是如何支持这些能力的。
我们来看一下QMetaObject的定义，我们先看一下QMetaObject对象中包含的成员数据。
我们都知道，把一个signal和slot连接起来，需要使用QObject类的connect方法，它的作用就是把一个object的signal和另外一个object的slot连接起来，以达到对象间通讯的目的。
当我们写下一下emit signal代码的时候，与这个signal相连接的slot就会被调用，那么这个调用是如何发生的呢？让我们来逐一解开其中的谜团。
很多C/C++初学者常犯的一个错误就是，使用malloc、new分配了一块内存却忘记释放，导致内存泄漏。Qt的对象模型提供了一种Qt对象之间的父 子关系..
首先，让我们来看看Qt/e的系统结构介绍：Qt for destop Linux 和 Qt for Embedded Linux 最大的区别就在于他们所依赖的底层显示基础的不同，这也就导致了他们在体系结构上的差异。
本输入法设计指南针对Qt for Embedded Linux 4.5.1，并且以中文输入法为例做说明，并且本文只是侧重于说明Qt/Embedded对输入法的支持接口，
前面我们介绍了Qte输入法的基本设计思路，以及一个最简单的例子，那么，Qte的输入法是如何工作的呢？本节我们就来看一下Qte的源代码，一起来解开这个谜团。
Part 4：移动平台开发
Symbian S60
Forum Nokia Qt for Mobile Developers training
09年10月21至23号，某人参加了诺基亚在北航举办的Qt开发培训。培训师是来自于芬兰的Niemi Petri，英语比好多芬兰人要好，课程讲得深入浅出，很好理解。课程内容涉及Qt的基本知识，以及Qt在S60和Maemo上的开发。下面是培训的PPT和作业以及演示代码。
Maemo
转自：http://www.qteverywhere.com/learnqt
为了做毕设，决定速学Qt.今天简单地实现了下Qt教程中的简单程序，Qt + c++ 才是王道啊。
什么是最优化，可分为几大类？
答：Levenberg-Marquardt算法是最优化算法中的一种。最优化是寻找使得函数值最小的参数向量。它的应用领域非常广泛，如：经济学、管理优化、网络分析、最优设计、机械或电子设计等等。
根据求导数的方法，可分为2大类。第一类，若f具有解析函数形式，知道x后求导数速度快。第二类，使用数值差分来求导数。
根据 使用模型不同，分为非约束最优化、约束最优化、最小二乘最优化。
什么是Levenberg-Marquardt算法？
它是使用最广泛的非线性最小二乘算法，中文为列文伯格-马夸尔特法。它是利用梯度求最大（小）值的算法，形象的说，属于“爬山”法的一种。它同时具有梯度 法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。在作者的科研项目中曾经使用过多次。图1显示了算法从起 点，根据函数梯度信息，不断爬升直到最高点（最大值）的迭代过程。共进行了12步。（备注：图1中绿色线条为迭代过程）。
图1 LM算法迭代过程形象描述
图1中，算法从山脚开始不断迭代。可以看到，它的寻优速度是比较快的，在山腰部分直接利用梯度大幅度提升（参见后文例子程序中lamda较小时），快到山顶时经过几次尝试（lamda较大时），最后达到顶峰（最大值点），算法终止。
如何快速学习LM算法？
学 习该算法的主要困难是入门难。 要么国内中文教材太艰涩难懂，要么太抽象例子太少。目前，我看到的最好的英文入门教程是K. Madsen等人的《Methods for non-linear least squares problems》本来想把原文翻译一下，贴到这里。请让我偷个懒吧。能找到这里的读者，应该都是E文好手，我翻译得不清不楚，反而事倍功半了。
可在 下面的链接中找到
http://www2.imm.dtu.dk/pubdb/public/publications.php? year=&pubtype=7&pubsubtype=§ion=1&cmd=full_view&lastndays=&order=author
或者直接下载pdf原文：
http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf
例子程序（MATLAB源程序）
本程序不到100行，实现了 求雅克比矩阵的解析解，Levenberg-Marquardt最优化迭代，演示了如何求解拟合问题。采用《数学试验》（第二版）中p190例2来演示。在MATLAB中可直接运行得到最优解。
|
% 计算函数f的雅克比矩阵，是解析式
syms a b y x real;
f=a*exp(-b*x);
Jsym=jacobian(f,[a b])
% 拟合用数据。参见《数学试验》，p190，例2
data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
obs_1=[19.21 18.15 15.36 14.10 12.89 9.32 7.45 5.24 3.01];
% 2. LM算法
% 初始猜测s
a0=10; b0=0.5;
y_init = a0*exp(-b0*data_1);
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=2;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;
% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;
% step2: 迭代
for it=1:n_iters
if updateJ==1
% 根据当前估计值，计算雅克比矩阵
J=zeros(Ndata,Nparams);
for i=1:length(data_1)
J(i,:)=[exp(-b_est*data_1(i)) -a_est*data_1(i)*exp(-b_est*data_1(i))];
end
% 根据当前参数，得到函数值
y_est = a_est*exp(-b_est*data_1);
% 计算误差
d=obs_1-y_est;
% 计算（拟）海塞矩阵
H=J'*J;
% 若是第一次迭代，计算误差
if it==1
e=dot(d,d);
end
end
% 根据阻尼系数lamda混合得到H矩阵
H_lm=H+(lamda*eye(Nparams,Nparams));
% 计算步长dp，并根据步长计算新的可能的\参数估计值
dp=inv(H_lm)*(J'*d(:));
g = J'*d(:);
a_lm=a_est+dp(1);
b_lm=b_est+dp(2);
% 计算新的可能估计值对应的y和计算残差e
y_est_lm = a_lm*exp(-b_lm*data_1);
d_lm=obs_1-y_est_lm;
e_lm=dot(d_lm,d_lm);
% 根据误差，决定如何更新参数和阻尼系数
if e_lm<e
lamda=lamda/10;
a_est=a_lm;
b_est=b_lm;
e=e_lm;
disp(e);
updateJ=1;
else
updateJ=0;
lamda=lamda*10;
end
end
%显示优化的结果
a_est
b_est
|
本程序对应的C++实现，待整理后于近期公开。
转自：
http://www.shenlejun.cn/my/article/show.asp?id=17&page=1
最短路中，求出源到各点的最短路。如果a->b有一条边，那么dis[a]+w(a,b)>=dis[b].
将所有的条件转化成边即可。
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int maxn=1010;
const int maxm=1000000;
const int INF=1000000000;
struct node
{
int t;
int w;
node *next;
}edge[maxm],*adj[maxn];
int len=0;
void init(int n)
{
for(int i=0;i<n;i++)
adj[i]=NULL;
len=0;
}
void addedge(int u,int v,int w)
{
edge[len].t=v;edge[len].w=w;edge[len].next=adj[u];adj[u]=&edge[len++];
}
int dis[maxn];//[0,n-1]
int use[maxn];
int cnt[maxn];
bool SPFA(int n,int s)
{
queue<int>Q;
fill(dis,dis+n,INF);
fill(use,use+n,0);
fill(cnt,cnt+n,0);
dis[s]=0;
use[s]=1;
Q.push(s);
while(!Q.empty())
{
int x=Q.front();Q.pop();
use[x]=0;
++cnt[x];
if(cnt[x]>n)return false;
for(node *p=adj[x];p;p=p->next)
{
int t=p->t,w=p->w;
if(dis[x]+w<dis[t])
{
dis[t]=dis[x]+w;
if(!use[t])
{
Q.push(t);
use[t]=1;
}
}
}
}
return true;
}
int main()
{
int ca;
scanf("%d",&ca);
while(ca--)
{
int n,x,y;
scanf("%d%d%d",&n,&x,&y);
init(n);
for(int i=0;i<x;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
a--;b--;
addedge(a,b,c);
}
for(int i=0;i<y;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
a--;b--;
addedge(b,a,-c);
}
//for(int i=0;i<n-1;i++)
// addedge(i+1,i,0);
if(!SPFA(n,0))printf("-1\n");
else if(dis[n-1]==INF)printf("-2\n");
else printf("%d\n",dis[n-1]);
}
return 0;
}
给出N,e,d，3<=e<31,求出p,q;
二分给BigInteger开方很好用。
另外就是枚举(p-1)*(q-1)在比赛的时候也不失为一种很不错的方法。
import java.math.*;
import java.util.*;
import java.io.*;
public class Main
{
public static BigInteger Sqrt(BigInteger x)
{
BigInteger l=new BigInteger("0");
BigInteger r=x;
while(l.compareTo(r)<0)
{
BigInteger mid=l.add(r).divide(BigInteger.valueOf(2));
if(mid.multiply(mid).compareTo(x)<0)
l=mid.add(BigInteger.ONE);
else if(mid.multiply(mid).compareTo(x)==0)
return mid;
else
r=mid.subtract(BigInteger.ONE);
}
return l;
}
public static boolean Judge(BigInteger x)
{
BigInteger tem=new BigInteger("0");
tem=Sqrt(x);
if(tem.multiply(tem).compareTo(x)==0)
return true;
else
return false;
}
public static void main(String[] args)
{
Scanner cin = new Scanner (new BufferedInputStream(System.in));
String sn;
String se;
String sd;
int ca=0;
while(true)
{
ca++;
sn=cin.next();
se=cin.next();
sd=cin.next();
BigInteger n=new BigInteger(sn);
BigInteger e=new BigInteger(se);
BigInteger d=new BigInteger(sd);
if(n.compareTo(BigInteger.ZERO)==0 && e.compareTo(BigInteger.ZERO)==0 &&d.compareTo(BigInteger.ZERO)==0)
break;
for(int i=1;i<=100;i++)
{
BigInteger t=e.multiply(d).subtract(BigInteger.ONE).divide(BigInteger.valueOf(i));
BigInteger t2= t.subtract(n).subtract(BigInteger.ONE).pow(2).subtract(BigInteger.valueOf(4).multiply(n));
if(Judge( t2 )==true)
{
t2=Sqrt(t2);
// System.out.println(t2);
BigInteger p=n.subtract(t).add(BigInteger.ONE).add(t2).divide(BigInteger.valueOf(2));
BigInteger q=n.subtract(t).add(BigInteger.ONE).subtract(t2).divide(BigInteger.valueOf(2));
if(q.compareTo(p)<0)
{
BigInteger mm=q;
q=p;
p=mm;
}
System.out.println("Case #"+ca+":"+" "+p+" "+q);
break;
}
}
}
}
}
摘要: 题意：有n(<=20)只队伍比赛, 队伍i初始得分w[i], 剩余比赛场数r[i](包括与这n只队伍以外的队伍比赛), mat[i][j]表示队伍i与队伍j剩余比赛场数, 没有平局, 问队伍0有没有可能获得这n队中的第一名(可以有并列第一). 做法1：其实第一个队可以不用管它了,n支队我们将它压缩到n-1。//球队编号[0,n-2]//比赛数[n-1,n-2+id]//超级源n-1+id//...
阅读全文