|
|
2010年11月13日
来源与分析: http://chenjianneng3.blog.163.com/blog/static/128345126201033101044920/因为是求极值,所以要注意所求的数据范围,特别是最大,最小可能值。
2010 成都赛区的 Error Curves 就是典型的三分:
附上我的程序:
 
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 10010;
const double eps = 1e-8;
double a[maxn],b[maxn],c[maxn];
int n;
double cal(double x)
{
double s = -1e100,tmp;//注意s的要尽量小
for (int i = 1; i <= n; i++)
{
tmp = a[i]*x*x + b[i]*x + c[i];
s = max(tmp,s);
}
return s;
}
void solve()
{
double left = 0.0, right = 1000.0;
double mid, midmid;
double mid_v, midmid_v;
while (left + eps < right)
{
mid = (left + right) / 2;
midmid = (mid + right) / 2;
mid_v = cal(mid);
midmid_v = cal(midmid);
if (mid_v < midmid_v)
right = midmid;
else left = mid;
}
printf("%.4lf\n",cal((left+right)/2));
}
int main()
{
int t,i,j;
scanf("%d",&t);
while (t--)
{
scanf("%d",&n);
for (i = 1; i <= n; i++)
scanf("%lf %lf %lf",&a[i],&b[i],&c[i]);
solve();
}
return 0;
}
某某程序:
 
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 10086;
double a[MAXN], b[MAXN], c[MAXN];
int main() {
int re, n;
double l, r, m1, m2, y1, y2;
scanf("%d", &re);
for (int ri = 1; ri <= re; ++ri) {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("%lf%lf%lf", &a[i], &b[i], &c[i]);
}
l = 0;
r = 1000;
while (r - l > 1e-8) {
m1 = (l * 2 + r) / 3;
m2 = (l + r * 2) / 3;
y1 = y2 = -1e100;
for (int i = 0; i < n; ++i) {
y1 = max(y1, (a[i] * m1 + b[i]) * m1 + c[i]);
y2 = max(y2, (a[i] * m2 + b[i]) * m2 + c[i]);
}
if (y1 < y2) {
r = m2;
} else {
l = m1;
}
}
l = (l + r) / 2;
r = -1e100;
for (int i = 0; i < n; ++i) {
r = max(r, (a[i] * l + b[i]) * l + c[i]);
}
printf("%.4lf\n", r);
}
return 0;
}
三分法小结:只要解在一点范围内满足凸函数性质就行,通俗点说就是两边夹,从两边不断逼近。
模版化:
double Cal(Type a)
{
/* 根据题目的意思计算 */
}
void Solve(void)
{
double Left, Right;
double mid, midmid;
double mid_value, midmid_value;
Left = MIN; Right = MAX;
while (Left + EPS < Right)
{
mid = (Left + Right) / 2;
midmid = (mid + Right) / 2;
mid_value = Cal(mid);
midmid_value = Cal(midmid);
// 假设求解最大极值.
if (mid_value >= midmid_value) Right = midmid;
else Left = mid;
}
}
poj3301cpp代码:
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const double PI = acos(-1.0);
const double eps = 1e-8;
const double maxn = 1000;
int n;
double x[35],y[35];
double cal(double a)
{
double bx ,by ,sx,sy;
bx = by = -maxn ,sx = sy = maxn;
double tx,ty;
for (int i = 1; i <= n; i++)
{
//tx,ty为坐标变换后的坐标,具体怎么推得忘了????
tx = x[i] * cos(a) - y[i] * sin(a);
ty = y[i] * cos(a) + x[i] * sin(a);
bx = max(tx,bx);
sx = min(tx,sx);
by = max(ty,by);
sy = min(ty,sy);
}
return max(bx - sx , by - sy);
}
int main()
{
int t,i,j;
double lf,rt;
double m1,m2;
double m1_v,m2_v;
scanf("%d",&t);
while (t--)
{
scanf("%d",&n);
for (i = 1; i <= n; i++)
scanf("%lf %lf",&x[i],&y[i]);
lf = 0.0; rt = PI/2;
while (lf + eps < rt)
{
m1 = (lf + rt) / 2;
m2 = (m1 + rt) / 2;
m1_v = cal(m1);
m2_v = cal(m2);
if (m1_v <= m2_v)
rt = m2;
else lf = m1;
}
double len = cal(lf);
printf("%.2lf\n",len*len);
}
return 0;
}
摘要: 题目描述:
给定n 个字符串,求出现在不小于k 个字符串中的最长子串。
解题报告:
将n 个字符串连起来,中间用不相同的且没有出现在字符串中的字符隔开,求后缀数组。然后二分答案,将后缀分成若干组,判断每组的后缀是否出现在不小于k 个的原串中。
注意: 1、题目要求是超过一半有最大的公共子串,即 》 N / 2,并且 N = 1时直接输出; &n... 阅读全文
2010年11月5日
//rmq 求得最大最小值的序号。
// 注意位运算优先级比+低。
//被字母(l)和 数字(1)搞了半天,最后终于看出来了
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAX = 50005;
int rmqMin[MAX][20],rmqMax[MAX][20];
int n,q;
void make_rmq(int len,int a[])
{
int i,j,k,x1,y1,x2,y2;
for (i = 1; i <= len; i++)
rmqMin[i][0] = rmqMax[i][0] = i;
for (j = 1; (1 << j) <= len; j++)
for (i = 1; i + (1 << j) - 1 <= len; i++)
{
x1 = rmqMin[i][j-1];
y1 = rmqMin[i + (1<<(j-1))][j-1];
x2 = rmqMax[i][j-1];
y2 = rmqMax[i + (1<<(j-1))][j-1];
rmqMin[i][j] = a[x1] < a[y1] ? x1 : y1;
rmqMax[i][j] = a[x2] > a[y2] ? x2 : y2;
}
}
int query_min(int lf,int rt,int a[])
{
int d = rt - lf + 1,k = 0,x,y;
while ((1<<(k+1)) < d)
k ++;
x = rmqMin[lf][k];
y = rmqMin[rt - (1 << k) + 1][k];
return a[x] < a[y] ? x : y;
}
int query_max(int lf,int rt,int a[])
{
int d = rt - lf + 1, k = 0, x, y;
while ((1<<(k+1)) < d)
k++;
x = rmqMax[lf][k];
y = rmqMax[rt - (1<<k) + 1][k];
return a[x] > a[y] ? x : y;
}
int main()
{
int he[MAX],i,lf,rt;
while (scanf("%d %d", &n, &q) != EOF)
{
for (i = 1; i <= n ; i++)
scanf("%d", &he[i]);
make_rmq(n,he);
for (i = 1; i <= q; i++)
{
scanf("%d %d", &lf, &rt);
printf("%d\n",he[query_max(lf,rt,he)] - he[query_min(lf,rt,he)]);
}
}
return 0;
}
2010年10月29日
题意:自己看吧。 分析:对左边的点从小到大排序,相等则对右边的从小到大排,最后只要求左边的逆序对即可,求逆序对除了树状数组还有归并排序。 注意:边可以达到1000*1000,结果会超int。 cpp代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int maxn,n,m,k;
struct Point{
int x,y;
}a[1000010];
long long c[1005];
int Lowbit(int i)
{
return i&(-i);
}
long long up(int x)
{
int i = x;
long long res = 0;
while (i <= maxn)
{
res += c[i];
i += Lowbit(i);
}
return res;
}
void down(int x)
{
int i = x;
while (i > 0)
{
c[i]++;
i -= Lowbit(i);
}
}
bool cmp(const Point &a,const Point &b)
{
if (a.x == b.x)
return a.y < b.y;
return a.x < b.x;
}
int main()
{
int t,cas = 1,i;
long long ans;
scanf("%d ", &t);
while (t--)
{
ans = 0;
scanf("%d %d %d",&n,&m,&k);
for (i = 1; i <= m; i++)
c[i] = 0;
maxn = m;
for (i = 1; i <= k; i++)
{
scanf("%d %d",&a[i].x, &a[i].y);
}
sort(a+1, a+1+k, cmp);
for (i = 1; i <= k; i++)
{
ans += up(a[i].y + 1);
down(a[i].y);
}
printf("Test case %d: %I64d\n",cas++, ans);
}
return 0;
}
题意:给每只cow的头尾坐标,求对于每只cow比他壮的cow,壮大的定义就是比他长就是比他壮。 分析:二维变一维,先按左边的坐标按 j 从大到小排列,然后是 i 左边的坐标从小到大,最后处理 i 就行了,跟stars一样。 cpp代码:
#include <cstdio>
#include <stdlib.h>
#include <algorithm>
#include <memory.h>
using namespace std;
int maxn;
int c[100010];
struct Cow{
int s,e;
int id;
}cow[100010];
int cnt[100010];
int n;
bool cmp(const Cow &a,const Cow &b)
{
if (a.e == b.e)
return a.s < b.s;
return a.e > b.e;
}
int Lowbit(int i)
{
return i&(-i);
}
void up(int x)
{
int i = x;
while (i <= n)
{
c[i] += 1;
i += Lowbit(i);
}
}
int down(int x)
{
int i = x , res = 0;
while (i > 0)
{
res += c[i];
i -= Lowbit(i);
}
return res;
}
int main()
{
int i,x,y;
while (scanf("%d",&n) && n)
{
maxn = 0;
memset(c,0,sizeof(c));
for (i = 1; i <= n ;i++)
{
cnt[i] = 0;
scanf("%d %d",&x,&y);
cow[i].s = x+1 , cow[i].e = y+1;
cow[i].id = i;
if (maxn < cow[i].e)
maxn = cow[i].e;
}
sort(cow+1,cow+1+n,cmp);
for (i = 1; i <= n;i++)
{
if (i > 1 && cow[i].s == cow[i-1].s && cow[i].e == cow[i-1].e)
cnt[cow[i].id] = cnt[cow[i-1].id];
else cnt[cow[i].id] = down(cow[i].s);
up(cow[i].s);
}
for (i = 1; i <= n; i++)
{
if (i != 1)
printf(" ");
printf("%d",cnt[i]);
}
printf("\n");
}
return 0;
}
题意:给一个二维矩阵,边修改点格的手机的改变数目,边查询区间手机的总数目。 分析:就是Matrix的相反操作。 CPP代码:
#include <iostream>
#include <cstdio>
using namespace std;
int n;
int c[1030][1030];
int Lowbit(int i)
{
return i&(-i);
}
void up(int x,int y,int a)
{
int i = x,j;
while (i <= n)
{
j = y;
while (j <= n)
{
c[i][j] += a;
j += Lowbit(j);
}
i += Lowbit(i);
}
}
int down(int x,int y)
{
int i = x,j,res = 0;
while (i > 0)
{
j = y;
while (j > 0)
{
res += c[i][j];
j -= Lowbit(j);
}
i -= Lowbit(i);
}
return res;
}
int main()
{
int ins,x,y,x1,y1,a;
int i,j;
scanf("%d %d",&ins,&n);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
c[i][j] = 0;
while (1)
{
scanf("%d",&ins);
if (ins == 3)
break;
if (ins == 1)
{
scanf("%d %d %d",&x,&y,&a);
x++,y++;
up(x,y,a);
}
if (ins == 2)
{
int ans = 0;;
scanf("%d %d %d %d",&x,&y,&x1,&y1);
x++,y++,x1++,y1++;
ans = down(x1,y1) - down(x1,y-1) - down(x-1,y1) + down(x-1,y-1);
printf("%d\n",ans);
}
}
return 0;
}
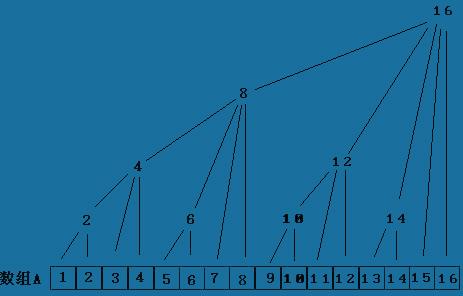
题意:自己看吧。 分析:终于通过这道题弄懂了树状数组。 首先这里我不具体解释 int Lowbit() { i + (- i ) } 来源,我只想 强调的是数组C【i】保存的是C[i - 2^k +1] 到C[i] 区间的状态,k 值是 i 二进制表示中末尾0的个数。 我的理解就是树状数组有两种操作down ,up,都是对区间状态的操作,或者点状态的操作,注意一点的就是只是状态(包括简单的和,个数的
统计,本题翻转次数的统计)的查询与修改。树状数组的结构就是多叉树形结构,up(即 i + Lowbit(i))是逐级向上处理父区间(注意我说的是父区间),
down (即:i - Lowbit(i))要注意的是 down 不是逐级向下找子区间并进行操作,而是找左边相邻的兄弟区间(我不知道这样描述准不准确,
你可以看那张经典的树状数组的结构图再自己算算就很明了了)。正因为这样,树状数组能方便的查询父区间(UP操作),而不能方便的访问子区间,
只能方便访问左边相邻的兄弟区间(down操作),我觉得这就是它相对于线段树的不足之处,不过还是很强大的了。
所以,当遇到具体的问题时,只要记住只是区间状态(和,个数,翻转次数。。。。)的访问,具体的操作是用down还是up就很好理解了。
对于本题,change时是对区间段的翻转次数进行修改所以是down(依次向左对兄弟区间进行修改),当Query时,其实就是统计点覆盖点(x,y)各区间的总翻转次数所以是向上(up)查询父区间的过程,你可以自己模拟一下就很明了。
 实现的CPP代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 1005
int mat[N][N];
int n;
int lowbit(int key){
return key&(-key);
}
int getsum(int x, int y){
int ans = 0;
for(int i=x; i<=n; i+=lowbit(i))
for(int j=y; j<=n; j+=lowbit(j))
ans = (ans+mat[i][j])%2;
return ans;
}
void change(int x, int y){
for(int i=x; i>0; i-=lowbit(i))
for(int j=y; j>0; j-=lowbit(j))
mat[i][j] = (mat[i][j]+1)%2;
}
int main(){
int t;
char si[10];
scanf("%d",&t);
while(t--){
int m;
scanf("%d%d",&n,&m);
memset(mat,0,sizeof(mat));
for(int i=0; i<m; i++){
scanf("%s",si);
if(si[0]=='C'){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
change(x2,y2);
change(x1-1,y2);
change(x2,y1-1);
change(x1-1,y1-1);
}else{
int x1,y1;
scanf("%d%d",&x1,&y1);
printf("%d\n",getsum(x1,y1));
}
}
printf("\n");
}
return 0;
}
具体的就不多解释了,当线段树练练手吧。
#include <cstdio>
#include <stdlib.h>
#include <cmath>
#include <algorithm>
using namespace std;
const int root = 0;
const double eps = 1e-8;
struct Node{
int l,r,cover;
int lnd,rnd;
double len;
}node[10000];
int cnt,cnty;
double indx[210];
struct Line{
double x,y1,y2;
bool f;
}line[210];
void Creat(int p,int l,int r)
{
node[p].l = l; node[p].r = r;
node[p].len = 0.0; node[p].cover = 0;
if (r - l > 1)
{
int mid = (l + r) >> 1;
node[p].lnd = ++cnt;
Creat(cnt,l,mid);
node[p].rnd = ++cnt;
Creat(cnt,mid,r);
}
else {node[p].lnd = node[p].rnd = -1;}
}
void upData(int p)
{
if (node[p].cover > 0)
{
node[p].len = indx[node[p].r] - indx[node[p].l];
}
else if (node[p].l == node[p].r - 1)
{
node[p].len = 0.0;
node[p].cover = 0;
}
else {
int lf = node[p].lnd;
int rf = node[p].rnd;
node[p].len = node[lf].len + node[rf].len;
}
}
void Insert(int p,int l,int r)
{
// printf("p = %d,[%d,%d]\n",p,l,r);
if (l <= node[p].l && node[p].r <= r)
node[p].cover++;
else {
int mid = (node[p].l + node[p].r) >> 1;
if (mid > l)
Insert(node[p].lnd,l,r);
if (mid < r)
Insert(node[p].rnd,l,r);
}
upData(p);
}
void Delete(int p,int l,int r)
{
if (l <= node[p].l && node[p].r <= r)
node[p].cover--;
else {
int mid = (node[p].l + node[p].r) >> 1;
if (mid > l)
Delete(node[p].lnd,l,r);
if (mid < r)
Delete(node[p].rnd,l,r);
}
upData(p);
}
int Bi_Search(double key)
{
int l = 1,r = cnty + 1,mid;
while (l < r)
{
mid = (l + r) >> 1;
if (fabs(indx[mid] - key) < eps)
return mid;
else if (indx[mid] + eps < key)
l = mid + 1;
else r = mid;
}
}
void Init_Index()
{
sort(indx+1,indx+1+cnty);
int m = 1;
for (int i = 2; i <= cnty; i++)
if (fabs(indx[i] - indx[i-1]) > eps)
{
// printf("%lf \n",indx[i]);
m ++;
indx[m] = indx[i];
}
cnty = m;
}
bool cmp(const Line &a,const Line &b)
{
return a.x < b.x;
}
int main()
{
int n,i,j,k,left,right,cas = 1;
double x1,x2,y1,y2,prelen,ans,ny1,ny2;
while (scanf("%d",&n) && n)
{
for (i = 1; i <= n + n; i+=2)
{
scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);
ny1 = min(y1,y2);
ny2 = max(y2,y1);
line[i].x = x1; line[i].y1 = ny1; line[i].y2 = ny2;
line[i].f = true;
line[i+1].x = x2; line[i+1].y1 = ny1; line[i+1].y2 = ny2;
line[i+1].f = false;
indx[i] = y1; indx[i+1] = y2;
}
sort(line+1,line+1+n+n,cmp);
cnty = n + n;
Init_Index();
// printf("cnty = %d\n",cnty);
Creat(root,1,cnty);
left = Bi_Search(line[1].y1);
right = Bi_Search(line[1].y2);
Insert(root,left,right);
prelen = node[root].len;
ans = 0;
for (i = 2; i <= n+n ;i++)
{
left = Bi_Search(line[i].y1);
right = Bi_Search(line[i].y2);
if (line[i].f)
Insert(root,left,right);
else Delete(root,left,right);
ans += prelen*(line[i].x - line[i-1].x);
prelen = node[root].len;
// printf("i = %d,len = %lf\n",i,prelen);
}
printf("Test case #%d\n",cas++);
printf("Total explored area: %.2lf\n\n",ans);
}
return 0;
}
题意:给星星的坐标,定义每个星星左下角(包括正左边和正上方)的星星数是它的level,统计各个level的星星数。
分析:乍看是个二维的统计,因为数据给出的是 y坐标升序,y相等 x坐标升序,所以可以一次读入数据,只要统计 x左边的星星数就行了,
这道题很好的启示就是二维降一维的方法————按某种规则排序。
下面给出了线段树和树状数组的写法。
点线段树cpp代码如下:
#include <cstdio>
#include <algorithm>
using namespace std;
const int root = 0;
struct Node{
int l,r,cnt;
int lnd,rnd;
}node[60005];
int cnt,cntx;
int indx[15010];
int x[15010],y[15010];
void Creat(int p,int l,int r)
{
node[p].l = l; node[p].r = r;
node[p].cnt = 0;
if (l < r)
{
int mid = (l + r) >> 1;
node[p].lnd = ++cnt;
Creat(cnt,l,mid);
node[p].rnd = ++cnt;
Creat(cnt,mid+1,r);
}
else {node[p].lnd = node[p].rnd = -1;}
}
void upData(int p)
{
if (node[p].l < node[p].r)
node[p].cnt = node[node[p].lnd].cnt + node[node[p].rnd].cnt;
}
void Insert(int p,int id)
{
if (id == node[p].l && id == node[p].r)
node[p].cnt++;
else {
int mid = (node[p].l + node[p].r) >> 1;
if (mid < id)
Insert(node[p].rnd,id);
else Insert(node[p].lnd,id);
}
upData(p);
}
int query(int p,int l,int r)
{
int ans = 0;
if (l <= node[p].l && node[p].r <= r)
ans = node[p].cnt;
else{
int mid = (node[p].l + node[p].r) >> 1;
if (mid >= l)
ans += query(node[p].lnd,l,r);
if (mid < r)
ans += query(node[p].rnd,l,r);
}
return ans;
}
int Bi_Search(int key)
{
int l = 1,r = cntx+1,mid;
while (l < r)
{
mid = (l + r) >> 1;
if (indx[mid] == key)
return mid;
else if (indx[mid] < key)
l = mid + 1;
else r = mid;
}
}
void Init_Index()
{
sort(indx+1,indx+1+cntx);
// for (int i = 1; i <= cntx; i++)
// printf("%d,",indx[i]);
int m = 1;
for (int i = 2; i <= cntx; i++)
{
if (indx[i] != indx[i-1])
{
m++;
indx[m] = indx[i];
}
}
cntx = m;
}
int main()
{
int n,i,j,k,id;
int count[15010];
while (scanf("%d",&n) != EOF)
{
for (i = 1; i <= n; i++)
{
count[i] = 0;
scanf("%d %d",&x[i],&y[i]);
indx[i] = x[i];
}
// for (i = 1; i <= n ;i++)
// printf("%d ",indx[i]);
// printf("\n");
cntx = n;
Init_Index();
/* for (i = 1; i <= cntx; i++)
printf("%d ",indx[i]);
printf("cntx = %d\n",cntx);*/
cnt = 0;
Creat(root,1,cntx);
for (i = 1; i <= n; i++)
{
id = Bi_Search(x[i]);
// printf("id = %d\n",id);
k = query(root,1,id);
// printf("i = %d,k = %d\n",i,k);
count[k] ++;
Insert(root,id);
}
for (i = 0; i < n; i++)
printf("%d\n",count[i]);
}
return 0;
}
树状数组的cpp代码:
#include<stdio.h>
int a[32002];
int level[15000];
int N;
int lowbit(int n){
return n&(-n);
}
int Sum(int n)
{
int result = 0;
while(n!=0){
result+=a[n];
n-=lowbit(n);
}
return result;
}
void Update(int n)
{
while(n<=32001){
a[n]++;
n+=lowbit(n);
}
}
void init()
{
int i;
for(i=0;i<=N;i++)
level[i]=a[i]=0;
}
int main()
{
int x,y,i;
scanf("%d",&N);
i=N;
init();
while(i--){
scanf("%d %d",&x,&y);
level[Sum(x+1)]++;
Update(x+1);
}
for(i=0;i<N;i++)
printf("%d\n",level[i]);
}
题意就不多说了。 分析:就是把poj1177简单改动就行了。 总结:出错时输出看看prelen对不对就行了。
#include <cstdio>
#include <stdlib.h>
#include <algorithm>
using namespace std;
const int root = 0;
struct Node{
int l,r,cover;
int cnt,len;
int lf,rf;
int lnd,rnd;
}node[200010];
int cnt,cnty;
int indx[80010];
struct Line{
int x,y1,y2;
bool f;
} line[80010];
void Creat(int p ,int l,int r)
{
node[p].l = l; node[p].r = r;
node[p].len = node[p].cnt = node[p].cover = 0;
node[p].lf = node[p].rf = 0;
if(r - l > 1)
{
int mid = (l + r) >> 1;
node[p].lnd = ++cnt;
Creat(cnt,l,mid);
node[p].rnd = ++cnt;
Creat(cnt,mid,r);
}
else {node[p].lnd = -1; node[p].rnd = -1;}
}
void upData(int p)
{
if (node[p].cover > 0)
{
node[p].len = indx[node[p].r] - indx[node[p].l];
node[p].cnt = 1;
node[p].lf = node[p].rf = 1;
}
else if (node[p].l == node[p].r -1)
{
node[p].cover = 0;
node[p].len = 0;
node[p].lf = node[p].rf = node[p].cnt = 0;
}
else {
int left = node[p].lnd;
int right = node[p].rnd;
node[p].len = node[left].len + node[right].len;
node[p].lf = node[left].lf;
node[p].rf = node[right].rf;
node[p].cnt = node[left].cnt + node[right].cnt - node[left].rf*node[right].lf;
}
}
void Insert(int p,int l,int r)
{
if(l <= node[p].l && node[p].r <= r)
node[p].cover ++;
else {
int mid = (node[p].l + node[p].r) >> 1;
if(mid > l)
Insert(node[p].lnd,l,r);
if (mid < r)
Insert(node[p].rnd,l,r);
}
upData(p);
}
void Delete(int p,int l,int r)
{
if(l <= node[p].l && node[p].r <= r)
node[p].cover--;
else {
int mid = (node[p].l + node[p].r) >> 1;
if(mid > l)
Delete(node[p].lnd,l,r);
if (mid < r)
Delete(node[p].rnd,l,r);
}
upData(p);
}
bool cmp(const Line &a,const Line &b)
{
return a.x < b.x;
}
int Bi_Search(int key)//二分查找
{
int l = 1,r = cnty+1,mid;
while (l < r)
{
mid = (l + r) >> 1;
if(indx[mid] == key)
return mid;
else if(indx[mid] < key)
l = mid + 1;
else r = mid;
}
}
void Init_Index()//离散化(排序= 去重
{
sort(indx+1,indx+1+cnty);
int m = 1;
for (int i = 2; i <= cnty; i++)
if(indx[i] != indx[i-1])
{
m++;
indx[m] = indx[i];
}
cnty = m;
}
int main()
{
int n,i,j;
long long ans;
int x,y,h,prelen,left,right;
while (scanf("%d",&n) != EOF)
{
cnty = 1;
indx[cnty] = 0;
for (i = 1; i <= n+n; i+=2)
{
scanf("%d %d %d",&x,&y,&h);
line[i].x = x; line[i].y1 = 0; line[i].y2 = h;
line[i].f = true;
line[i+1].x = y; line[i+1].y1= 0; line[i+1].y2 = h;
line[i+1].f = false;
indx[++cnty] = h;
}
sort(line+1,line+1+n+n,cmp);
Init_Index();
cnt = 0;
Creat(root,1,cnty);
left = 1;
right = Bi_Search(line[1].y2);
Insert(root,left,right);
prelen = node[root].len;
ans = 0;
//printf("1 .len = %d\n",prelen); .len = %d\n",prelen);
for (i = 2; i <= n+n; i++)
{
left = 1;
right = Bi_Search(line[i].y2);
if (line[i].f)
Insert(root,left,right);
else Delete(root,left,right);
//注意 long long
ans += (long long)prelen*((long long)line[i].x - (long long)line[i-1].x);
prelen = node[root].len;
/****************检查出错很好的手段************************/
//printf("i = %d .len = %d\n",i,prelen); .len = %d\n",i,prelen);
}
printf("%I64d\n",ans);
}
return 0;
}
|