随笔档案

IDT

异常和硬件中断

Spurious IRQs

PIT

中断处理结束

分页

分页前后

物理内存管理

内存管理器初始化之前

编译和使用

Tunnel逻辑结构

Rust的使用感受

Bootloader

我们知道计算机启动是从BIOS开始，再由BIOS决定从哪个设备启动以及启动顺序，比如先从DVD启动再从硬盘启动等。计算机启动后，BIOS根据配置找到启动设备，并读取这个设备的第0个扇区，把这个扇区的内容加载到0x7c00,之后让CPU从0x7c00开始执行，这时BIOS已经交出了计算机的控制权，由被加载的扇区程序接管计算机。

这第一个扇区的程序就叫Boot，它一般做一些准备工作，把操作系统内核加载进内存，并把控制权交给内核。由于Boot只能有一个扇区大小，即512字节，它所能做的工作很有限，因此它有可能不直接加载内核，而是加载一个叫Loader的程序，再由Loader加载内核。因为Loader不是BIOS直接加载的，所以它可以突破512字节的程序大小限制（在实模式下理论上可以达到1M）。如果Boot没有加载Loader而直接加载内核，我们可以把它叫做Bootloader。

Bootloader加载内核就要读取文件，在实模式下可以用BIOS的INT 13h中断。内核文件放在哪里，怎么查找读取，这里牵涉到文件系统，Bootloader要从硬盘（软盘）的文件系统中查找内核文件，因此Bootloader需要解析文件系统的能力。GRUB是一个专业的Bootloader，它对这些提供了很好的支持。

对于一个Toy操作系统来说，可以简单处理，把内核文件放到Bootloader之后，即从软盘的第1个扇区开始，这样我们可以不需要支持文件系统，直接读取扇区数据加载到内存即可。

实模式到保护模式

我们知道Intel x86系列CPU有实模式和保护模式，实模式从8086开始就有，保护模式从80386开始引入。为了兼容，Intel x86系列CPU都支持实模式。现代操作系统都是运行在保护模式下（Intel x86系列CPU）。计算机启动时，默认的工作模式是实模式，为了让内核能运行在保护模式下，Bootloader需要从实模式切换到保护模式，切换步骤如下：

1. 准备好GDT(Global Descriptor Table)
2. 关中断
3. 加载GDT到GDTR寄存器
4. 开启A20，让CPU寻址大于1M
5. 开启CPU的保护模式，即把cr0寄存器第一个bit置1
6. 跳转到保护模式代码

GDT是Intel CPU保护模式运行的核心数据结构，所有保护模式操作的数据都从GDT表开始查找，这里有GDT的详细介绍。

GDT中的每一个表项由8字节表示，如下图：

其中Access Byte和Flags如下图：

这里是详细说明。

GDTR是一个6字节的寄存器，有4字节表示GDT表的基地址，2字节表示GDT表的大小，即最大65536（实际值是65535，16位最大值是65535），每个表项8字节，那么GDT表最多可以有8192项。

实模式的寻址总线是20bits，为了让寻址超过1M，需要开启A20，可以通过以下指令开启：

    in al, 0x92
    or al, 2
    out 0x92, al

把上述步骤完成之后，我们就进入保护模式了。在保护模式下我们要使用GDT通过GDT Selector完成，它是GDT表项相对于起始地址的偏移，因此它的值一般是0x0 0x8 0x10 0x18等。

ELF文件

Bootloader程序是原始可执行文件，如果程序由汇编写成，汇编编译器编译生成的文件就是原始可执行文件，也可以使用C语言编写，编译成可执行文件之后通过objcopy转换成原始可执行文件，这篇文章介绍了用C语言写Bootloader。

那么内核文件是什么格式的呢？跟Bootloader一样的当然可以。内核一般使用C语言编写，每次编译链接完成之后调用objcopy是可以的。我们也可以支持通用的可执行文件格式，ELF(Executable and Linkable Format)即是一种通用的格式，它的维基百科。

ELF文件有两种视图（View），链接视图和执行视图，如下图：

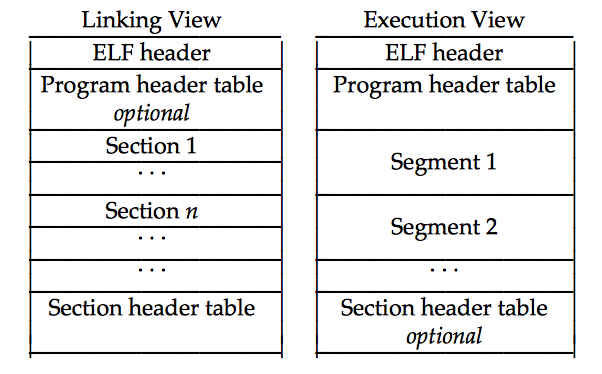
链接视图通过Section Header Table描述，执行视图通过Program Header Table描述。Section Header Table描述了所有Section的信息，包括所在的文件偏移和大小等；Program Header Table描述了所有Segment的信息，即Text Segment, Data Segment和BSS Segment，每个Segment中包含了一个或多个Section。

对于加载可执行文件，我们只需关注执行视图，即解析ELF文件，遍历Program Header Table中的每一项，把每个Program Header描述的Segment加载到对应的虚拟地址即可，然后从ELF header中取出Entry的地址，跳转过去就开始执行了。对于ELF格式的内核文件来说，这个工作就需要由Bootloader完成。Bootloader支持ELF内核文件加载之后，用C语言编写的内核编译完成之后就不需要objcopy了。

为什么写操作系统

首先是兴趣，在现在这个时代，写操作系统几乎没有实用价值，只能是一个Toy，在写一个Toy OS时，可以学习掌握很多知识，并把这些知识贯穿实用起来。操作系统是一个复杂的系统，牵涉到的东西很多，我相信写操作系统可以帮助理解现代操作系统及其它底层知识。我目前才刚开始写，代码放在Github上。

    // |-----|--------|---------------|-----|-------------|
    // | any | repeat | capture begin |  | capture end |
    // |-----|--------|---------------|-----|-------------|

class ASTNode
{
public:
    ACCEPT_VISITOR() = 0;
    virtual ~ASTNode() { }
};
 
class CharNode : public ASTNode
{
public:
    explicit CharNode(int c) : c_(c) { }
 
    ACCEPT_VISITOR();
 
    int c_;
};
 
class CharRangeNode : public ASTNode
{
public:
    struct Range
    {
        int first_;
        int last_;

        explicit Range(int first = 0, int last = 0)
            : first_(first), last_(last)
        {
        }
    };

    CharRangeNode() { }

    void AddRange(int first, int last)
    {
        ranges_.push_back(Range(first, last));
    }
 
    void AddChar(int c)
    {
        chars_.push_back(c);
    }
 
    ACCEPT_VISITOR();
 
    std::vector<Range> ranges_;
    std::vector<int> chars_;
};
 
class ConcatenationNode : public ASTNode
{
public:
    void AddNode(std::unique_ptr<ASTNode> node)
    {
        nodes_.push_back(std::move(node));
    }
 
    ACCEPT_VISITOR();
 
    std::vector<std::unique_ptr<ASTNode>> nodes_;
};
 
class AlternationNode : public ASTNode
{
public:
    void AddNode(std::unique_ptr<ASTNode> node)
    {
        nodes_.push_back(std::move(node));
    }
 
    ACCEPT_VISITOR();
 
    std::vector<std::unique_ptr<ASTNode>> nodes_;
};
 
class ClosureNode : public ASTNode
{
public:
    explicit ClosureNode(std::unique_ptr<ASTNode> node)
        : node_(std::move(node))
    {
    }
 
    ACCEPT_VISITOR();
 
    std::unique_ptr<ASTNode> node_;
};

class EdgeSetConstructorVisitor : public Visitor
{
public:
    explicit EdgeSetConstructorVisitor(EdgeSet *edge_set)
        : edge_set_(edge_set)
    {
    }
 
    EdgeSetConstructorVisitor(const EdgeSetConstructorVisitor &) = delete;
    void operator = (const EdgeSetConstructorVisitor &) = delete;
 
    VISIT_NODE(CharNode);
    VISIT_NODE(CharRangeNode);
    VISIT_NODE(ConcatenationNode);
    VISIT_NODE(AlternationNode);
    VISIT_NODE(ClosureNode);

private:
    EdgeSet *edge_set_;
};

最近几个月利用上下班的时间在学习Haskell，Haskell有不少让人开阔思路的东西，也有不少看起来很美好，用起来不错，但是读起来费劲的东西。Haskell的语法学的差不多了之后，用Haskell写了一个简单的C++代码行统计工具，写过几个版本，留下了两个，一个是直接用模式匹配写的，一个是山寨了一个极简的parse combinator，然后用这个山寨的parse combinator写了一个版本，代码估计写的都比较烂，以后进阶学习之后有时间再改。这个统计工具并不是完整的处理C++的语法，也没对在字符串和宏定义里面的"//" "/*" "*/"做处理，因此对某些C++程序统计代码行，可能不完全正确，但是基本可以用。

data, type, newtype

Haskell里面用data来定义数据类型，它可以是这样：
 

第一行定义了一个Mode，包含ReadMode和WriteMode；

第二行定义了一个普通数据类型Some，包含一个Int数据和一个String数据；

第三行定义了一个普通数据类型Thing，包含类型为Int的a和类型为String的b；

第四行定义了一个符合数据类型Func，里面有个函数类型为(a -> b)的数据func。

第一种相当于C++中的enum class，第二种第三种相当于普通的struct数据，第二种和第三种的区别是第二种不能直接取到Int和String的数据，第三种可以通过a,b取到数据，第四种相当于C++的template class(struct)，第四种写成这样来定义具体的数据类型：

type在这里定义了一个别名IntStringFunc类型，包含了一个函数类型是Int -> String的func的数据，这里的type相当于C++ 11的using别名，因为它还可以这样写：

在C++ 11中，using包含了typedef的功能，也支持了template class的类型typedef，如下：

newtype定义的数据类型跟type类型，不过type定义的纯粹是别名，别名类型跟原始类型是一致的，而newtype则定义的是一个wrapper，是一种新的数据类型，所以是newtype。newtype定义的类型是编译时期的wrapper，Haskell保证没有运行时期的开销，newtype定义的跟data类似：

模式匹配

上面说道data定义的第二种数据类型，包含Int和String的数据，但是不能直接取到这两个数据，所以我们需要定义两个函数来取其中的数据：

这里的getSomeInt和getSomeString函数都是采用模式匹配来实现，模式匹配就是把数据的结构直接写在代码中来匹配，然后取出想要使用的数据即可。

Haskell里常用的Maybe数据类型是这样定义的：

如果要取用Maybe里面的值，我们通常使用模式匹配来获取数据，如下：

下面调用useMaybe的函数体内取到的a的值就是1。

Haskell里的内置数据类型list，比如[1, 2, 3, 4]，使用:可以把新的元素添加到list头部，即：

这样的特性同样可以简单的套用在模式匹配上面，如下：

useList [] = 
useList (x:xs) = … -- x是list里面的第一个元素，xs是list的尾部

模式匹配可以很直观的匹配数据的原始表示方式，并可以取出其中有用的值做其他操作，它是一个简单直观有效的操作数据的方式，甚至可以在嵌套很深的tuple数据里面直接取出想要的数据，而不用像C++那样调用tuple::get之类的函数来取出其中的值，比如：

Visitor模式和C++ template

王垠说设计模式中值得一提的模式不多，其中之一的visitor模式是在模拟模式匹配。visitor模式通常是访问获取某个继承类层次构成的一个树形结构中的某个节点的具体类型，并对这种具体类型做某些操作，而模式匹配是可以从复杂的数据结构中直接取出想要的数据。

C++的template meta-programming也可以看成是一种模式匹配，C++里面著名的Factorial求值是这样的：

而这段代码如果用Haskell写是这样的：

C++中的模板参数就是用来做模式匹配的，每特化一种类型就可以匹配某种类型，然后对那种匹配的类型做相应的操作。C++的template meta-programming是编译时期（编译器运行期）的行为，所以它只能操作类型以及编译时期能够确定的值，而模式匹配是程序本身的运行期的行为。

Currying

Haskell的Currying是一个很有用的特性，但是我觉得这个特性滥用的话，也会让程序代码的可读性降低不少。所谓Currying就是可以向一个多参数的函数传递比它所需的参数个数更少的参数后返回生成的一个新函数接受剩余的参数的函数。Haskell里的函数默认都是curried的，所以Haskell里面的函数可以随意currying，比如：

Currying的实现是使用的单参数的lambda构成的闭包(closure)，add可以看成是接受一个Int参数返回一个函数，这个函数的类型是Int -> Int。

Partial application

Currying是一个从左到右部分传参数的一个过程，也就是不会出现参数a还没给，就给了具体的参数b的情况。如果确定要先给参数b，那么它是Partial application，如下：

(+ 2)这种类似的用法可能会作为参数传递给另外一个函数。Partial application是一种更宽泛的概念，上面的Currying是一种Partial application。

正如王垠所说的，如果一个函数接受了多个参数，但是这个函数在实际调用中被Currying了很多次，那最后生成的那个函数它到底接受几个参数是不能很直观的看明白的，比如：

那当我们看到do5函数的时候，我们是很难判断do5到底接受几个参数，尤其是do5跟前面几个doN函数不在同一个地方定义，很有可能do5只是传递给某个函数的参数，当然如果给每个函数都加上函数类型声明会清晰许多。当Currying碰到了flip之后，那代码的可读性会降低更多，所以我觉得Currying是一个很有用的特性，但是如果被滥用的话，那代码的可读性会是一个问题。

C++: function + bind

C++中的function + bind其实是一种Partial application实现，比如：

我觉得C++的function + bind会比Currying的可读性要好一些，毕竟我们可以完整看到f1和f2的函数类型，知道参数类型及个数和返回值，是有利于代码的可读性的，当然这里完全可以不写出f1和f2的类型，采用auto，我们同样可以从调用函数bind的placeholder的个数得知bind之后的function的参数个数，这样我们可以不用看到函数Func的声明，就知道需要传几个参数。function + bind跟Currying一样会影响代码的可读性，如果嵌套的层次越多，可读性就越差，所以使用这些特性的时候不要过度。

typeclass

Haskell用typeclass来表示一个concept，它是一组抽象函数的集合，一个满足某个typeclass的数据类型，它就可以跟其他使用这个typeclass的函数或者数据类型组合使用。typeclass一般这么定义：

它定义了一个叫Monad的typeclass，这个typeclass的concept里有四个函数，分别是(>>=), (>>), return和fail，m是一个带类型参数的数据类型。我们上面知道了Maybe是一个带类型参数的data类型，它定义如下：

既然Maybe是一个带类型参数的data，那它就满足Monad typeclass中m的需求，因此可以把Maybe定义成Monad，如下：

这里(\_ -> maybeB)定义了一个lambda，参数 _ 紧接 \，-> 后面则是函数体。函数(>>)和fail是可以作为默认实现放到class Monad的定义里面，而instance Monad的时候只需要实现(>>=)和return即可。

对于内置list类型[a]，也是带有一个类型参数a，因此，我们同样可以把[] instance成为class Monad，如下：

函数(>>)和fail我们保留默认的实现即可。

Monad

上面实现的定义的typeclass就是Haskell著名的Monad，它是组合其他操作的一个基础typeclass，是与no pure交互的一个重要媒介。一般情况下Monad有两种，一种是数据wrapper，一种是action的wrapper。上面定义的Maybe Monad和list Monad都是数据类型的wrapper，它们实现了Monad定义的接口函数，我们还可以将其它data instance成Monad，只需要遵循了Monad的接口即可。

我们知道Haskell的函数都是pure的，没有任何状态的函数，但是与现实世界交互必然需要影响或修改某种状态，并且会需要顺序执行某些操作以完成交互。我们把action操作封装在一个data里面，并让它instance Monad，为了让前一个action的结果值作为某种状态往下传递，Monad的(>>=)就是为了这个目的而存在的，(>>=) 函数的类型是 m a -> (a -> m b) -> m b，它的意思就是执行封装在m a这个数据里面的action，然后把这个action的结果值做为参数传递给(>>=)的第二个参数(a -> m b)，第二个参数是一个函数，这函数可以取用第一个参数的结果，再返回一个m b的数据，m b的数据也是一个action的封装，这样当一连串的(>>=)放到一起的时候，就可以把一个状态值作为action的参数和结果值往下传递。

从Monad的函数(>>)的实现我们可以看到，它把m a的action的结果值丢弃直接返回了m b，当一连串的(>>)放到一起的时候，其实就是让一组action顺序执行。通过(>>=)和(>>)，可以把一组Monad action data组合起来。

IO Monad

IO Monad是一个把IO action封装的data，我们可以使用IO Monad与外界进行输入输出交互，下面是一个"hello world"：

这里do语法糖其实就是用的Monad来实现，展开之后是这样：

由(>>)函数确定(putStr "hello ")和(putStrLn "world")需要是同一个Monad类型，我们可以查询到putStr和putStrLn的类型是String -> IO ()，那么(putStr "hello ")和(putStrLn "world")的类型都是IO ()，helloWorld函数把两个IO ()的action数据顺序组合起来生成一个新的IO ()，当这个helloWorld IO action被执行的时候，它会依次执行封装在它里面的IO action。我们可以把helloWorld IO action放到Main函数里面然后编译执行，也可以直接在ghci里面执行。

我们可以自己定义某种data再instance Monad，这样可以构成一组data combination，可以实现任意的action combine。我山寨的极简的parse combinator的数据类型定义如下：

这里Parser带一个类型参数a，deriving (Monad, MonadState (ByteString, Context))表示编译器自动instance Monad和instance MonadState (ByteString, Context)。有了这个Parser之后，可以写出简单的几个combinator，然后使用这几个combinator组合成更加复杂的，组合的过程就是利用了Monad的组合能力。当所需的combinator都实现了好了之后，可以最终实现一个Parser a来分析整个C++文件：

file就把分析整个C++文件所需的操作都combine到了一起，有了这个分析整个文件的Parser a之后，需要把它跑起来，那就需要定义下面这个函数：

这个函数接受一个Parser a和一个文件内容ByteString作为参数，把整个Parser a封装的action用于分析文件内容，再产生一个分析结果。

这里的file，它是一个一个小的combinator构成的，每个combinator是一个action加上它所需数据构成一个“闭包”再存放到Parser a的data里面，其实可以认为实现了Monad的数据类型是一个“闭包”的载体。在其它语言里，我们可以使用闭包来实现combinator，我记得两年半前，我使用lua的闭包实现了一组游戏副本内容玩法操作的combinator，这些闭包自由组合在一起之后就能完成一个副本中所需的玩法操作。

Monad transformer

一种Monad类型只能封装和组合一种action操作，而与外界交互的时候，很多时候一种Monad类型是不够的，为了让多种Monad类型组合在一起，就需要定义Monad transformer，它跟Monad一样也是一个数据类型，不同的是它接受至少两种类型参数，其中一种就是Monad的类型，这样就可以把某个Monad类型嵌套在它里面。

这里StateT就是一个Monad transformer，它允许嵌套一个Monad m类型，它是typeclass MonadState的一个instance，MonadState如下：

为了让Monad transformer可以嵌套进StateT，其它类型的Monad transformer就需要instance MonadState，而StateT Monad transformer为了可以嵌套在其它Monad transformer中，就需要对其它Monad transformer抽象出来的typeclass instance，符合这种规则的Monad transformer就可以相互之间嵌套了，嵌套的层次可以任意深，这样构造出来的Monad里面有个Monad transformer stack，而这个新构造出来的Monad就可以使用多种Monad的action操作组合在一起了。

Monad transformer会带来一个问题，如果想定义一个新的Monad transformer，需要先抽象出这个Monad transformer的typeclass，就像MonadState typeclass一样，然后把其它Monad transformer都instance这个新抽象出来的typeclass，这样才能让这个新的Monad transformer嵌套在其它的Monad transformer之中，接着，为了让其它Monad transformer能够嵌套在新的Monad transformer之中，需要把新的Monad transformer instance其它Monad transformer抽象的typeclass。

我觉得其实Haskell为什么会有Monad和Monad transformer的存在，是因为Haskell是一个纯函数式语言，它本身没有顺序执行语句的能力，为了能让Haskell拥有修改外部状态并能够顺序执行语句的能力，引入了Monad，又为了让多种action的Monad能够组合到一起，由于Monad是一个data type，它不能简单的组合到一起，因为类型不一致，为了让它们组合到一起，又引入了更一般化的Monad transformer，让这些Monad transformer嵌套在一起构成一个stack，才能将这些不同类型的Monad组合。

Lazy evaluation

Haskell里面使用的是惰性求值方式，王垠说Haskell的惰性求值是一个很严重的问题。我目前也觉得惰性求值是一种负担，因为惰性求值，会使得程序很容易就出现space leak，我写的那两个版本的统计C++代码行工具都有这个问题，因为它是惰性求值，所以它会把整个目录的数据全部取出来构造存放到内存中，最后再进行求值，这就自然导致统计大量C++代码文件的目录时，占用内存会很高（几百M上G），也许当我进一步学习之后，我能够避免这种space leak，但这对于一个初学Haskell的人是一个不小的负担，因为随便写一个小程序都有可能耗用几百M的内存，而用其他语言实现的话，内存很容易很自然的控制在几M之内。（看完优化章节，只对程序修改了几行代码就让内存使用降到可以接受的程度，看来Lazy evaluation的问题没之前想像的那么严重。）