之前一端时间由于一些原因停顿了dx的学习，最近开始继续学习了，为了入门我还是从简单的地形写起。目标是实现地形的功能有分块处理，四叉树进行剪裁，lod，多纹理等。重开始看一些资料到现在也一个多星期了，但是实现的也只有地形分块，基于四叉树剪裁，lod这几个功能纹理还没顾上呢。每次写dx程序对渲染管线都有不太的理解。这个过程中有很多痛苦的东西来处理虽然明白了这些东西的人会觉得很容易但是，从不明白到理解这是一个过程，这个过程必须得自己走过才知道。为了让自己能在学习中不断积累，所以在只完成了部分的功能下记录我在写这些东西中碰到的一些问题。
    首先困扰我的是地形是否分块，我最开始看的资料是地形不分块，每个格子都是一个四叉树的叶子结点，在遍历四叉树的过程中进行块的可见性的检测和确定lod的，其方法大概如下：
1，从树根root开始检测
2，如果可见则继续递归检测其子结点
3，判断结点是否可见
3.1，可见并且就lod满足要求，则把这个结点作为一个格子的可渲染物加入到渲染队列中。
3.2，可见但是lod不符号要求则跳入到2.
3.2，不可见则放弃对这结点的子结点的遍历。
以上方法是我看资料时理解的，如果你不小心看到此文则最好再查找资料来看看 网上很多:)
按理来说如果一个513*513的地图，则这个四叉树也就有513*513结点，这个数据应该是比较庞大的，对这些数据做剪裁也是消耗比较大的。
    所以可以把地图分块，如一个513*513的地图可以分为一个33*33，这样这个四叉树就只有16*16个叶子结点了对地块的可见性检查就更加快速了。获得可见的地块后再根据规则确定每个地块的lod值。然后根据lod值给每给地块计算顶点索引。
归纳一下我的设计和实现的思路：
1 确定地图和地块的大小：
  如：地图大小为129*129，地块为17*17 则一共有8*8个地图块
2 创建四叉树：
  每个四叉树的结点结构为:
  

struct CQuadtreeNode
{
     CQuadtreeNode()
    {
       m_child[0] = m_child[1] = m_child[2] = m_child[3] = NULL;
    }
    
    CQuadtreeNode* m_child[4];            //节点的四个孩子节点
    int m_nCenterX, m_nCenterZ;           //节点的中心位置
    int m_nHalfReange;                    //节点的半径
    float DeltaH;                         //节点误差值
    int id;                               //记录节点id为叶子结点作用
};

ProduceTree(pNode)
{
  if(pNode is NULL)
 {
    return ;
  }
  else if(pNode is leaf)
 {
    CreateTerrainBlock( );
  }
  else
 {
    ProduceTree(pNode->child1);
    ProduceTree(pNode->child2);
    ProduceTree(pNode->child3);
    ProduceTree(pNode->child4);
   }
}

3   一些其他操作 比如：为每一个块计算它的四个相邻快，其中是为了消除地块与地块之间由于lod值的不同导致的裂缝需要修补。

4  在每一帧的过程：
    更新摄像机
    对地形块进行裁剪获得可见的地块
    根据摄像机的距离计算这些可见地块的lod值
    对这些可见地块根据lod填充IB值
    对地块进行渲染。

    思路是很简单，但是实现过程比较麻烦现在我把一些东东记录下来。
    首先看看地形的大小，都是（2^n+1）*（2^n+1）的格式，这样规定的原因是为了四叉树的建立，2^n+1个顶点则有2^n个格。如一个33*33的地图，每个块的大小为17*17则这个树的一层。
    四叉树的结构比较简单，并且特定的为地形服务所以这就不记录了。
    平截体裁剪，这个也花费了很多时间去理解，先是要理解投影矩阵的目的是什么，在3D中投影矩阵是把平截体进行变化为一个范体，如何求解六个平面的算法网上有。这是我实现的代码:

    //计算出六个平截面，其中传递的参数是视图矩阵，所以平截面是在世界矩阵中
    void Calculate(D3DXMATRIX matView)
    {
        D3DXMATRIX mat = matView * m_matProj;
        //根据 mat * (A, B, C ,D) = (A1, B1, C1, D1)
        //具体方法原理网上可以查找到（投影矩阵的目的）
        //经过投影变换后平截体会变成范体变换后的六个面的方程易得：
        //near:  0x+0y+z+0=0;
        //far :  0x+0y-z+1=0;
        //left:  x+0y+0z+1=0;
        //right: -x+0y+0z+1=0;
        //bottom:0x+y+0z+1=0;
        //top:   0x-y+0z+1=0;

        //near plane;
        m_plane[0][0] = mat(0,2);
        m_plane[0][1] = mat(1,2);
        m_plane[0][2] = mat(2,2);
        m_plane[0][3] = mat(3,2);

        //far plane;
        m_plane[1][0] = mat(0,3)-mat(0,2);
        m_plane[1][1] = mat(1,3)-mat(1,2);
        m_plane[1][2] = mat(2,3)-mat(2,2);
        m_plane[1][3] = mat(3,3)-mat(3,2);

        //left plane;
        m_plane[2][0] = mat(0,3) + mat(0,0);
        m_plane[2][1] = mat(1,3) + mat(1,0);
        m_plane[2][2] = mat(2,3) + mat(2,0);
        m_plane[2][3] = mat(3,3) + mat(3,0);

        //right plane;
        m_plane[3][0] = mat(0,3) - mat(0,0);
        m_plane[3][1] = mat(1,3) - mat(1,0);
        m_plane[3][2] = mat(2,3) - mat(2,0);
        m_plane[3][3] = mat(3,3) - mat(3,0);

        //bottom plane;
        m_plane[4][0] = mat(0,3) + mat(0,1);
        m_plane[4][1] = mat(1,3) + mat(1,1);
        m_plane[4][2] = mat(2,3) + mat(2,1);
        m_plane[4][3] = mat(3,3) + mat(3,1);

        //top plane;
        m_plane[5][0] = mat(0,3) - mat(0,2);
        m_plane[5][1] = mat(1,3) - mat(1,2);
        m_plane[5][2] = mat(2,3) - mat(2,2);
        m_plane[5][3] = mat(3,3) - mat(3,2);
    
        //给六个平面的法向量规格化。这样就可以使得求点到面的距离很简单。
        //对应平面ax+by+cz+d=0; (a,b,c)则为平面的法向量
        for (int i = 0 ; i < 6; i++)
       {
            float len = sqrt(m_plane[i][0]*m_plane[i][0] +
                             m_plane[i][1]*m_plane[i][1] +
                             m_plane[i][2]*m_plane[i][2]);
            m_plane[i][0] /= len;
            m_plane[i][1] /= len;
            m_plane[i][2] /= len;
            m_plane[i][3] /= len;
        }
    }

有了平截体六个面的方程则检查一个物体是否与其相交就很容易了。具体的检查看你使用的地块的包围体是什么，如果是球体，则可以计算球心到每个面的距离与半径的关系来判断。
LOD 是细节程度值，比如一个9*9的顶点网格，可以划分为9*9，5*5，3*3，2*2这几个等级 ，当问9*9时则是全部顶点都画出，如果为5*5 则跳跃一个顶点，等等。

    由于当地块与地块的lod值不同时要对裂缝进行修补，修补的方法也有很多种，在《游戏编程精粹2》中就有篇文章介绍了一种。我使用的方法是动态的来计算IB。这个计算很麻烦也很烦琐。是一件比较痛苦的事情。

    很多细节的东西在这也很难写清楚，也许只有自己一步步走过来才有真正的体会
下面是两个程序运行的结果：

1.1

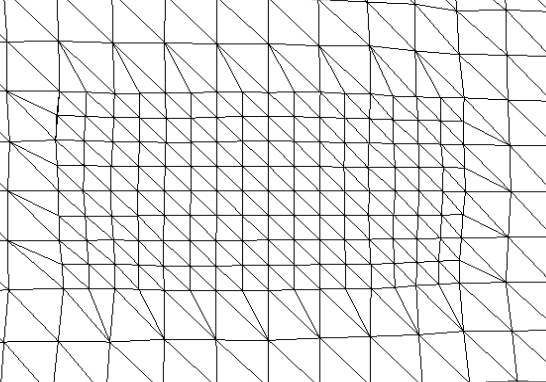
                            1.2俯视图

    现在的地图只是网格，还要很长的路，纹理 光照等到。很多东西也只有一步步来才能完成。呵呵如果你不小心看到了这文章，如果你觉得有问题请指点，如果也是像我一样是初学者请多参考一下其他人的写的，我的也只是看别人的资料写的，希望不会误导你，因为我写的目的只是为了一些记录。同时欢迎交流。
    继续走下去....