1. 逆序数
所谓逆序数，就是指一个序列S[i]，统计处于序列的每个数的比这个数大并且排在它前面的数的数目，然后对于所有数，把这个数目加起来求和就是了。
比如 4 3 1 2
4第一个，所以数目为0
3的前面是4，大于3的数目为1
1的前面是4 3 ，大于1的数目为2
2的前面是4 3 1，大于2的数目为2
所以逆序数为1+2+2 = 5
求逆序数的两种方法
常规方法是按照逆序数的规则做，结果复杂度是O(n*n)，一般来说，有两种快速的求逆序数的方法
分别是归并排序和树状数组法
2. 归并排序
归并排序是源于分而治之思想，详细的过程可以查阅其他资料，总体思想是划分一半，各自排好序后将两个有序序列合并起来。
如何修改归并排序求逆序数?
首先我们假设两个有序序列 a[i]和b[i]，当合并时：
由于a[i]已是有序，所以对于a[i]的各个元素来说，排在它前面且比它大的数目都是0
当b[i]中含有比a[i]小的元素时，我们必然将b[i]元素插到前面，那么就是说，在b[i]原先位置到该插的位置中，所有数都比b[i]大且排在它前面
所以这是b[i]的数目为新插入位置newPos - 原来位置oldPos
那么对于一半的序列又怎么做呢？我们知道，归并排序会继续向下递归，而递归完成返回后将是两组有序的序列，并且拿到局部的逆序数，
所以在Merge函数中添加这一计数操作即可
代码示例如下：
int L[M];
int R[M];
const int Max = 1 <<30;
__int64 change = 0;
void Merge(int *data,int left,int divide,int right)
{
int lengthL = divide - left;
int lengthR = right - divide;
for(int i = 0; i < lengthL; ++i)
{
L[i] = data[left + i];
}
for(int i = 0; i < lengthR; ++i)
{
R[i] = data[divide + i];
}
L[lengthL] = R[lengthR] = Max;
int i = 0;
int j = 0;
for(int k = left; k < right; ++k)
{
if(L[i] <= R[j])
{
data[k] = L[i];
++i;
}
else
{
change += divide - i - left ;
data[k] = R[j];
++j;
}
}
}
void MergeSort(int *data,int left,int right)
{
if(left < right -1)
{
int divide = (left + right)/2;
MergeSort(data,left,divide);
MergeSort(data,divide,right);
Merge(data,left,divide,right);
}
}
3. 树状数组
求逆序数的另外一种方法是使用树状数组
对于小数据，可以直接插入树状数组，对于大数据，则需要离散化，所谓离散化，就是将
100 200 300 400 500 ---> 1 2 3 4 5
这里主要利用树状数组解决计数问题。
首先按顺序把序列a[i]每个数插入到树状数组中，插入的内容是1，表示放了一个数到树状数组中。
然后使用sum操作获取当前比a[i]小的数，那么当前i - sum则表示当前比a[i]大的数，如此反复直到所有数都统计完，
比如
4 3 1 2
i = 1 : 插入 4 : update(4,1)，sum(4)返回1，那么当前比4大的为 i - 1 = 0;
i = 2 : 插入 3 : update(3,1)，sum(3)返回1，那么当前比3大的为 i - 1 = 1;
i = 3 : 插入 1 : update(1,1)，sum(1)返回1，那么当前比1大的为 i - 1 = 2;
i = 4 : 插入 2 : update(2,1)，sum(2)返回2，那么当前比2大的为 i - 2 = 2;
过程很明了，所以逆序数为1+2+2=5
代码示例如下：
//树状数组
__int64 sums[1005];
int len;
inline int lowbit(int t)
{
return t & (t^(t-1));
}
void update(int _x,int _value)
{
while(_x <= len)
{
sums[_x] += _value;
_x += lowbit(_x);
}
}
__int64 sum(int _end)//get sum[1_end]
{
__int64 ret = 0;
while(_end > 0)
{
ret += sums[_end];
_end -= lowbit(_end);
}
return ret;
}
//求逆序数
__int64 ret = 0;
for (__int64 i = 0; i < k; ++i)
{
update(a[i],1);
ret += (i+1) - sum(a[i]);
}
求逆序数的题目有：
http://poj.org/problem?id=2299
http://poj.org/problem?id=3067
posted @
2011-11-17 20:46 bennycen 阅读(10745) |
评论 (0) |
编辑 收藏
摘要: 题意：判断一个给定的图，没有环，而且存在一个链，图上的所有点或者在这条链上或者在其的邻居题解：1.判断环：对于无向图：如果 点 < 边 + 1，则存在环；然后使用并查集进一步判断环的存在2.判断是否存在链首先统计各个点的度，然后对于度为1的点，将其相连的边删掉，再统计新图的度，这时新图应该剩下一条链，也就是说，新图的不存在大于2个度为1的点，而且这个点在旧图的度是大于1的。代码：
Code...
阅读全文
posted @
2011-11-17 10:50 bennycen 阅读(5966) |
评论 (0) |
编辑 收藏
题意：烘干机，给出一堆衣服的水分a[i]，在不加烘干机情况下自动每一分钟减少1水分，每分钟可以变改衣服(i)到烘干机中，每分钟减少k水分，求最少需要多少时间。
题解：第一时间就想到使用二分枚据答案+验证这种思路，不过这题还是有些陷阱需要注意。
1. 验证答案时，如果 a[i] <= mid，让它自然烘干即可 ； 如果a[i] > mid，那么烘干这件衣服可以分成两段时间：使用烘干机时间x1 + 自然烘干时间x2，那么可以列出等式：mid = x1 + x2; a[i] <= kx1+x2；于是得x1 >= (a[i] -mid)/(k-1);即得使用烘干机的最少时间x1
2.注意当k==1时，k-1 == 0，需要特殊处理，直接打出ans = maxV
3.注意当求left+right时，结果可能超出范围，正确的方法应该是left + (right - left)*0.5;
#include <stdio.h>
const int N = 100005;
int n;
int a[N];
int k;
bool check(int _value)
{
int cnt = 0;
for (int i = 0; i < n; ++i)
{
if (a[i] > _value)
{
double kk = ((double)(a[i] - _value))/(k-1);
cnt += (int)kk;
if (kk - (int)kk > 0)
{
++cnt;
}
if (cnt > _value)
{
return false;
}
}
}
return (cnt <= _value);
}
int BinarySearch(int _low,int _high)
{
int left = _low;
int right = _high;
int mid;
int ans = _high;
while(left <= right)
{
mid = (left+(right-left)*0.5);
if (check(mid))
{
ans = mid;
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return ans;
}
void Test()
{
int maxV = 0;
for (int i = 0; i < n; ++i)
{
scanf("%d",&a[i]);
if (maxV < a[i])
{
maxV = a[i];
}
}
scanf("%d",&k);
if (k == 1)
{
printf("%d\n",maxV);
}
else
printf("%d\n",BinarySearch(0,maxV));
}
int main()
{
while(scanf("%d",&n) != EOF)
{
Test();
}
return 0;
}
posted @
2011-11-09 12:45 bennycen 阅读(1494) |
评论 (1) |
编辑 收藏
摘要: 大意：给出一个区域图和Click的坐标，求击中区域的周长题解：爆搜，BFS出整个连通域，注意求周长是上下左右的连通域，所以将8连域分成两个4连域，然后在BFS时一并计算出周长代码：
Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/-->#include&n...
阅读全文
posted @
2011-11-09 12:34 bennycen 阅读(1495) |
评论 (1) |
编辑 收藏
摘要: 题目大意：对以下数组：struct Cow { int score; int aid;}cows[C];共C个cow，选出N个(N为奇数)，使其aid的和在不大于给定的数F下，使这N个数的score的中位数最大。题解：依然使用堆，我们首先对牛的score进行排序，然后我们从第N/2头牛开始，到第C-N/2头牛结束。每次假设第i头牛就是中位数的牛，所以我们只需要计算这头牛的前N/...
阅读全文
posted @
2011-10-19 11:04 bennycen 阅读(2468) |
评论 (1) |
编辑 收藏
摘要: 编译过的二进制代码本身是一种数据结构，在代码被载入内存执行的时候，由操作系统对这种数据结构进行操作，具体到Win32平台，就是所谓的PE文件头。 对于Windows系统,源代码是如何转化为二进制代码?全局变量存储在什么地方,如何初始化?共享变量是如何工作?理解PE文件格式能更好地理解上面的问题.举个例子，我们使用C++编写源代码，这些源代码被编译器翻译成obj格式的目标文件，...
阅读全文
posted @
2011-09-02 20:18 bennycen 阅读(2329) |
评论 (2) |
编辑 收藏这几天研究了一下CUDA，发现其并行的思想和普通的CPU多线程思想不太一致，但还是挺不错。主要是将任务划分成一个个block，然后每个block里面再划分成细的线程。然后每个线程做自己做的
事情。这种并行思想很适用于像矩阵运算这些元素与元素之间的运算并不耦合得很厉害，但整体数据很大的情况，这只是我对CUDA的初步感觉。
矩阵相乘的CPU程序如下：
//C = A*B
void MatrixMulCPU(float* _C,const float *_A,const float *_B,int _wa,int _ha,int _wb)
{
float sum = 0;
for (int i = 0; i < _ha; ++i)
{
for (int j = 0; j < _wb; ++j)
{
sum = 0;
for (int k = 0; k < _wa; ++k)
{
sum += (float)_A[i*_wa+k]*(float)_B[k*_wb+ j];
}
_C[i*_wb+j] = (float)sum;
}
}
}
从上面可以看出，C(i,j) = sum { A(i,k)*B(k,j) } 0<=k < _wa;耦合程度很小，所以我们可以通过划分区域的方法，让每个线程负责一个区域。
怎么划分呢？首先最初的想法是让每一个线程计算一个C(i,j)，那么估算一下，应该需要height_c*width_c，也就是ha*wb个线程。进一步，我们将矩阵按一个大方格Grid划分，如果一个
方格Grid大小是16*16，那么矩阵80*48的可以表示为5(*16) * 3(*16)，即16*16个大格子(block)，每一个格子内，自然就是(height_c/16) *(width_c/16)个线程了。
好了，划分完后，内核代码如下：
计算版本0：
__global__ void matrix_kernel_0(float* _C,const float* _A,const float *_B,int _wa,int _wb)
{
float sum = 0;
//找出该线程所在的行列
int row = blockIdx.y*blockDim.y + threadIdx.y;
int col = blockIdx.x*blockDim.x + threadIdx.x;
//线程Thread(row,col)负责计算C(row,col)
for (int i = 0; i < _wa; ++i)
{
sum += _A[row*_wa + i]*_B[i*_wb + col];
}
_C[row*_wb + col] = sum;
}
另外一种思路，我们不让每一个线程完整计算一个C(i,j)，通过C(i,j) = sum { A(i,k)*B(k,j) }发现，我们还可以再细度划分：
Csub(i,j) = sum{A(i,ksub+offsetA)*B(ksub+offsetB,j)} 0<=ksub < blockSize
C(i,j) = sum{Csub(i,j)}
就是把矩阵分成n*n个大的子块，然后每一个block负责计算子块i 和 子块j的子乘积，计算完毕后加起来则可。这里主要使用了共享显存作优化。
计算版本1：
__global__ void matrix_kernel_1(float* _C,const float* _A,const float *_B,int _wa,int _wb)
{
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
//该block要处理的A
int aBegin = _wa*(by*BLOCK_SIZE);//A(0,by)
int aEnd = aBegin + _wa - 1;
int aStep = BLOCK_SIZE;//offsetA
int bBegin = BLOCK_SIZE*bx;//B(bx,0)
int bStep = BLOCK_SIZE*_wb;//offsetB
float cSub = 0;
for (int a = aBegin,b = bBegin; a <= aEnd; a += aStep,b += bStep)
{
__shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
__shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
//每个线程负责一个元素拷贝
As[ty][tx] = _A[a + _wa*ty + tx];
Bs[ty][tx] = _B[b + _wb*ty + tx];
__syncthreads();
//每个线程负责计算一个子块i 和 子块j的子乘积
for (int k = 0; k < BLOCK_SIZE; ++k)
{
cSub += As[ty][k]*Bs[k][tx];
}
__syncthreads();
}
//全局地址，向全局寄存器写回去
//一个线程负责一个元素，一个block负责一个子块
int cIndex = (by*BLOCK_SIZE + ty)*_wb + (bx*BLOCK_SIZE + tx);
_C[cIndex] = cSub;
}
最后写一个面向Host的接口函数：
void matrixMulGPU(float* _C,const float *_A,const float *_B,int _wa,int _ha,int _wb)
{
float* d_a = myNewOnGPU<float>(_wa*_ha);
float* d_b = myNewOnGPU<float>(_wb*_wa);
float* d_c = myNewOnGPU<float>(_wb*_ha);
copyFromCPUToGPU(_A,d_a,_wa*_ha);
copyFromCPUToGPU(_B,d_b,_wb*_wa);
dim3 threads(BLOCK_SIZE,BLOCK_SIZE);
dim3 blocks(WC/BLOCK_SIZE,HC/BLOCK_SIZE);
matrix_kernel_0<<<blocks,threads>>>(d_c,d_a,d_b,_wa,_wb);
cudaThreadSynchronize();
copyFromGPUToCPU(d_c,_C,_wb*_ha);
myDeleteOnGPU(d_a);
myDeleteOnGPU(d_b);
myDeleteOnGPU(d_c);
}
调用的主函数如下：
#include <stdio.h>
#include <cuda_runtime.h>
#include <cutil.h>
#include <cutil_inline.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <string.h>
#include <Windows.h>
#include "CUDACommon.h"
#include "MatrixMulCPU.h"
#include "MatrixMulGPU.h"
void randomInit(float* _data,int _size)
{
for (int i = 0; i < _size; ++i)
{
_data[i] = rand()/(float)RAND_MAX;
}
}
bool checkError(const float* _A,const float* _B,int _size)
{
for (int i = 0 ; i < _size; ++i)
{
if (fabs(_A[i] - _B[i]) > 1.0e-3)
{
printf("%f \t %f\n",_A[i],_B[i]);
return false;
}
}
return true;
}
int main(int argc, char* argv[])
{
srand(13);
if(!InitCUDA()) {
return 0;
}
float* A = myNewOnCPU<float>(WA*HA);
float* B = myNewOnCPU<float>(WB*HB);
randomInit(A,WA*HA);
randomInit(B,WB*HB);
float* C = myNewOnCPU<float>(WC*HC);
memset(C,0,sizeof(float)*WC*HC);
float* C2 = myNewOnCPU<float>(WC*HC);
memset(C2,0,sizeof(float)*WC*HC);
unsigned int tick1 = GetTickCount();
MatrixMulCPU(C2,A,B,WA,HA,WB);
printf("CPU use Time : %dms\n",GetTickCount() - tick1);
unsigned int timer = 0;
cutilCheckError(cutCreateTimer(&timer));
cutilCheckError(cutStartTimer(timer));
{
matrixMulGPU(C,A,B,WA,HA,WB);
}
cutilCheckError(cutStopTimer(timer));
printf("GPU use time: %f (ms) \n", cutGetTimerValue(timer));
cutilCheckError(cutDeleteTimer(timer));
if (checkError(C,C2,WC*HC))
{
printf("Accept\n");
}
else
{
printf("Worng Answer\n");
}
myDeleteOnCPU(A);
myDeleteOnCPU(B);
myDeleteOnCPU(C);
myDeleteOnCPU(C2);
return 0;
}
运算结果如下：
版本0：
版本1：
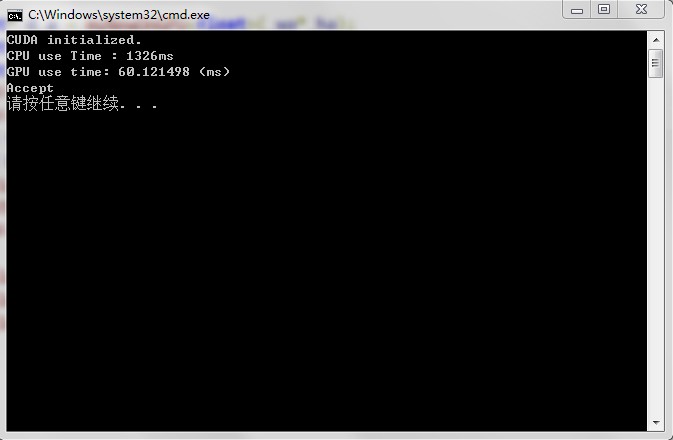
可以看出，GPU并行性能比CPU好很多，而且版本1优于版本0
整个工程下载：
/Files/bennycen/CUDAMatrixMul.rar
posted @
2011-07-26 17:01 bennycen 阅读(4602) |
评论 (1) |
编辑 收藏
题意：
给出两种操作：ADD(x)，将x添加到有序列表中；GET()返回全局迭代器所指的值，其中迭代器在GET操作后会自添加1
题解：
刚开始直接手打链表模拟，结果超时。这时应使用另外一种方法：使用大顶堆和小顶堆。
其中，对于序列S[1..n]，及表示迭代器位置的index，大顶堆维护排序后的S[1..index-1]，小顶堆维护
排序后的S[index..n],例如S[1..n] = 1,2,3,4,5,6,7，index = 4，则大顶堆为{1,2,3}，小顶堆为{4,5,6,7}
为什么要这样维护呢？因为当小堆最小的元素都大于大堆最大的元素时，那么序列中排第n个就是小堆最小的数了。
我们假设第k趟GET()后，有以下情景(GET后k自动加1)：
大顶堆：S[1..k]，堆顶元素为S[k]，小顶堆：S[k+1,n]，堆顶元素为S[k+1]，然后每当添加一个元素newE时，先添加到大顶堆中，这时如果出现大顶堆数大于小顶堆的数时，理应交换。
代码：
#include <queue>
#include <stdio.h>
using namespace std;
int m,n;
int sequence[30005];
struct cmp1
{
bool operator()(const int a,const int b)
{
return a>b;
}
};
struct cmp2
{
bool operator()(const int a,const int b)
{
return a<b;
}
};
void Test()
{
priority_queue<int,vector<int>,cmp1>q1;//小堆
priority_queue<int,vector<int>,cmp2>q2;//大堆
for (int i = 0; i < m; ++i)
{
scanf("%d",&sequence[i]);
}
int op;
int k = 0;
for (int i = 0; i < n; ++i)
{
scanf("%d",&op);
while(k < op)
{
q1.push(sequence[k]);
if (!q2.empty() && q1.top() < q2.top())
{
int t1 = q1.top();
q1.pop();
int t2 = q2.top();
q2.pop();
q1.push(t2);
q2.push(t1);
}
++k;
}
printf("%d\n",q1.top());
q2.push(q1.top());
q1.pop();
}
}
int main()
{
while(scanf("%d %d",&m,&n) != EOF)
{
Test();
}
return 0;
}
posted @
2011-06-02 15:34 bennycen 阅读(1691) |
评论 (0) |
编辑 收藏
摘要: 题意：如果单词A的结尾字母与单词B的首字母相同，那么可以认为是A到B相通。给出一系列单词，求这些词按照某种排列能否串通。题解：如果直接按照题意建模，以单词为顶点，边表示两两相通，那么将会得到哈密顿回路模型。显然是很难解的。换一种方式，以字母为顶点，边表示传送的单词，那么就得到欧拉回路模型的图，可以按照欧拉定理求解。以下给出Euler图的相关知识：Euler回路：G中经过每条边一次且仅一次的回路Eu...
阅读全文
posted @
2011-06-02 11:56 bennycen 阅读(1534) |
评论 (0) |
编辑 收藏
摘要: 题意：给出一个无向图，求在已知顶点v0的度不超过K的情况下，所得的最小生成树题解：首先不考虑v0点，先求得v1-v(n-1)的MST，然后分两种情况考虑：令d为v0的度情况1 ： 当d == 1，时 ，答案显然是min{edge(0,i)}+MST{v1-v(n-1)}当 1 < d <= K时，考虑逐步添加一条{0-i}边，添加边后势必构成回路，然后在回路中找到权值最大的边，然后在M...
阅读全文
posted @
2011-06-02 11:49 bennycen 阅读(1359) |
评论 (0) |
编辑 收藏