A*在游戏寻路算法里使用很广,可是感觉很多介绍它的文章故意让人看不懂。
仔细看了看gamedev.net的一片文章(A* Pathfinding for Beginners
http://www.gamedev.net/reference/articles/article2003.asp
),对A*更了解了一点,写点东西记录一下。
A*是一种启发式的算法,所谓的"启发式",就是对每一个搜索的位置进行评估,也就是把找的位置离目标的距离当成找点的一个依据,然后猜测这个点是否最佳("启发式"就是猜测)。
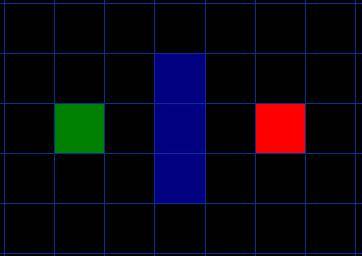
为了找到最佳的那个点
可以规定:
G = 从起点,沿着产生的路径,移动到网格上指定方格的距离。
H = 从网格上那个方格移动到终点B的预估移动距离。
F = G + H
F最小的点可以认为是该选的点。
引用一下原文的翻译:
我们令水平或者垂直移动的耗费为10,对角线方向耗费为14。我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号2(别怕),或者约1.414倍。为了简化,我们用10和14近似。比例基本正确,同时我们避免了求根运算和小数。
既然我们在计算沿特定路径通往某个方格的G值,求值的方法就是取它父节点的G值,然后依照它相对父节点是对角线方向或者直角方向(非对角线),分别增加14和10。例子中这个方法的需求会变得更多,因为我们从起点方格以外获取了不止一个方格。
H值可以用不同的方法估算。我们这里使用的方法被称为曼哈顿方法,它计算从当前格到目的格之间水平和垂直的方格的数量总和,忽略对角线方向。然后把结果乘以10。这被成为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数,在那里你不能沿对角线方向穿过街区。很重要的一点,我们忽略了一切障碍物。这是对剩余距离的一个估算,而非实际值,这也是这一方法被称为启发式的原因。想知道更多?你可以在这里找到方程和额外的注解。
第一步搜索的结果可以在下面的图表中看到。F,G和H的评分被写在每个方格里。正如在紧挨起始格右侧的方格所表示的,F被打印在左上角,G在左下角,H则在右下角。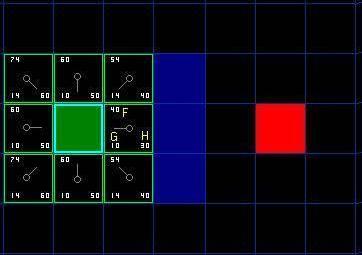
引用一下原文的翻译:
我们做如下操作开始搜索:
1,从点A开始,并且把它作为待处理点存入一个“开启列表”。开启列表就像一张购物清单。尽管现在列表里只有一个元素,但以后就会多起来。你的路径可能会通过它包含的方格,也可能不会。基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。也把他们加入开启列表。为所有这些方格保存点A作为“父方格”。当我们想描述路径的时候,父方格的资料是十分重要的。后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
为了继续搜索,我们简单的从开启列表中选择F值最低的方格。然后,对选中的方格做如下处理:
4,把它从开启列表中删除,然后添加到关闭列表中。
5,检查所有相邻格子。跳过那些已经在关闭列表中的或者不可通过的(有墙,水的地形,或者其他无法通过的地形),把他们添加进开启列表,如果他们还不在里面的话。把选中的方格作为新的方格的父节点。
6,如果某个相邻格已经在开启列表里了,检查现在的这条路径是否更好。换句话说,检查如果我们用新的路径到达它的话,G值是否会更低一些。如果不是,那就什么都不做。
另一方面,如果新的G值更低,那就把相邻方格的父节点改为目前选中的方格(在上面的图表中,把箭头的方向改为指向这个方格)。最后,重新计算F和G的值。如果这看起来不够清晰,你可以看下面的图示。

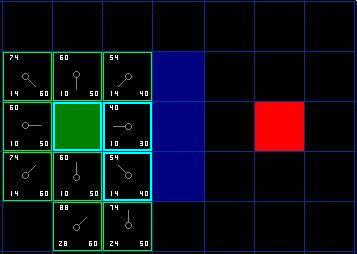
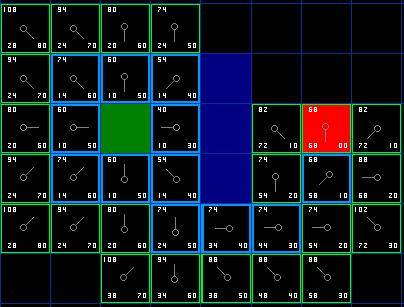
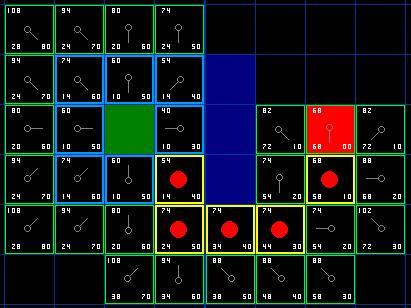
这样就可以找到最佳路径了。
在gameres上看见一个问题帖:
什么时候该用 Object object;
什么时候该用 Object *object;
object=new Object();
感觉看起来没什么区别,其实不一样:前一个是栈对象,后一个是堆对象。
引用一下别人对栈对象、堆对象的解释:
栈对象的优势是在适当的时候自动生成,又在适当的时候自动销毁,不需要程序员操心;而且栈对象的创建速度一般较堆对象快,因为分配堆对象时,会调用 operator new操作,operator new会采用某种内存空间搜索算法,而该搜索过程可能是很费时间的,产生栈对象则没有这么麻烦,它仅仅需要移动栈顶指针就可以了。但是要注意的是,通常栈空间容量比较小,一般是1MB~2MB,所以体积比较大的对象不适合在栈中分配。特别要注意递归函数中最好不要使用栈对象,因为随着递归调用深度的增加,所需的栈空间也会线性增加,当所需栈空间不够时,便会导致栈溢出,这样就会产生运行时错误。
堆对象,其产生时刻和销毁时刻都要程序员精确定义,也就是说,程序员对堆对象的生命具有完全的控制权。我们常常需要这样的对象,比如,我们需要创建一个对象,能够被多个函数所访问,但是又不想使其成为全局的,那么这个时候创建一个堆对象无疑是良好的选择,然后在各个函数之间传递这个堆对象的指针,便可以实现对该对象的共享。另外,相比于栈空间,堆的容量要大得多。实际上,当物理内存不够时,如果这时还需要生成新的堆对象,通常不会产生运行时错误,而是系统会使用虚拟内存来扩展实际的物理内存。
所以
当你知道你要使用的类型拥有准确数量时使用
Object object;当你不知道你要创建的类型有多少个时使用
Object *object;
object=new Object();
四元数常常可以在3D的书上看到。
但我的那本3D图形学书上,在没讲四元数是干什么的之前,就列了几张纸的公式,
大概因为自己还在上高中,不知道的太多,看了半天没看懂。。。
终于,在gameres上看到了某强人翻译的一个“4元数宝典 ”(原文是日本人写的。。。),感觉很好,分享下。
★旋转篇:
我将说明使用了四元数(si yuan shu, quaternion)的旋转的操作步骤
(1)四元数的虚部,实部和写法
所谓四元数,就是把4个实数组合起来的东西。
4个元素中,一个是实部,其余3个是虚部。
比如,叫做Q的四元数,实部t而虚部是x,y,z构成,则像下面这样写。
Q = (t; x, y, z)
又,使用向量 V=(x,y,z),
Q = (t; V)
也可以这么写。
正规地用虚数单位i,j,k的写法的话,
Q = t + xi + yj + zk
也这样写,不过,我不大使用
(2)四元数之间的乘法
虚数单位之间的乘法
ii = -1, ij = -ji = k (其他的组合也是循环地以下同文)
有这么一种规则。(我总觉得,这就像是向量积(外积),对吧)
用这个规则一点点地计算很麻烦,所以请用像下面这样的公式计算。
A = (a; U)
B = (b; V)
AB = (ab - U·V; aV + bU + U×V)
不过,“U·V”是内积,「U×V」是外积的意思。
注意:一般AB<>BA所以乘法的左右要注意!
(3)3次元的坐标的四元数表示
如要将某坐标(x,y,z)用四元数表示,
P = (0; x, y, z)
则要这么写。
另外,即使实部是零以外的值,下文的结果也一样。用零的话省事所以我推荐。
(4)旋转的四元数表示
以原点为旋转中心,旋转的轴是(α, β, γ)
(但 α^2 + β^2 + γ^2 = 1),
(右手系的坐标定义的话,望向向量(α, β, γ)的前进方向反时针地)
转θ角的旋转,用四元数表示就是,
Q = (cos(θ/2); α sin(θ/2), β sin(θ/2), γ sin(θ/2))
R = (cos(θ/2); -α sin(θ/2), -β sin(θ/2), -γ sin(θ/2))
(另外R 叫 Q 的共轭四元数。)
那么,如要实行旋转,
则 R P Q = (0; 答案)
请像这样三明治式地计算。这个值的虚部就是旋转之后的点的坐标值。
(另外,实部应该为零。请验算看看)
例子代码
/// Quaternion.cpp
/// (C) Toru Nakata, toru-nakata@aist.go.jp
/// 2004 Dec 29
#include <math.h>
#include <iostream.h>
/// Define Data type
typedef struct
{
double t; // real-component
double x; // x-component
double y; // y-component
double z; // z-component
} quaternion;
//// Bill 注:Kakezan 在日语里是 “乘法”的意思
quaternion Kakezan(quaternion left, quaternion right)
{
quaternion ans;
double d1, d2, d3, d4;
d1 = left.t * right.t;
d2 = -left.x * right.x;
d3 = -left.y * right.y;
d4 = -left.z * right.z;
ans.t = d1+ d2+ d3+ d4;
d1 = left.t * right.x;
d2 = right.t * left.x;
d3 = left.y * right.z;
d4 = -left.z * right.y;
ans.x = d1+ d2+ d3+ d4;
d1 = left.t * right.y;
d2 = right.t * left.y;
d3 = left.z * right.x;
d4 = -left.x * right.z;
ans.y = d1+ d2+ d3+ d4;
d1 = left.t * right.z;
d2 = right.t * left.z;
d3 = left.x * right.y;
d4 = -left.y * right.x;
ans.z = d1+ d2+ d3+ d4;
return ans;
}
//// Make Rotational quaternion
quaternion MakeRotationalQuaternion(double radian, double AxisX, double AxisY, double AxisZ)
{
quaternion ans;
double norm;
double ccc, sss;
ans.t = ans.x = ans.y = ans.z = 0.0;
norm = AxisX * AxisX + AxisY * AxisY + AxisZ * AxisZ;
if(norm <= 0.0) return ans;
norm = 1.0 / sqrt(norm);
AxisX *= norm;
AxisY *= norm;
AxisZ *= norm;
ccc = cos(0.5 * radian);
sss = sin(0.5 * radian);
ans.t = ccc;
ans.x = sss * AxisX;
ans.y = sss * AxisY;
ans.z = sss * AxisZ;
return ans;
}
//// Put XYZ into quaternion
quaternion PutXYZToQuaternion(double PosX, double PosY, double PosZ)
{
quaternion ans;
ans.t = 0.0;
ans.x = PosX;
ans.y = PosY;
ans.z = PosZ;
return ans;
}
///// main
int main()
{
double px, py, pz;
double ax, ay, az, th;
quaternion ppp, qqq, rrr;
cout << "Point Position (x, y, z) " << endl;
cout << " x = ";
cin >> px;
cout << " y = ";
cin >> py;
cout << " z = ";
cin >> pz;
ppp = PutXYZToQuaternion(px, py, pz);
while(1) {
cout << "\nRotation Degree ? (Enter 0 to Quit) " << endl;
cout << " angle = ";
cin >> th;
if(th == 0.0) break;
cout << "Rotation Axis Direction ? (x, y, z) " << endl;
cout << " x = ";
cin >> ax;
cout << " y = ";
cin >> ay;
cout << " z = ";
cin >> az;
th *= 3.1415926535897932384626433832795 / 180.0; /// Degree -> radian;
qqq = MakeRotationalQuaternion(th, ax, ay, az);
rrr = MakeRotationalQuaternion(-th, ax, ay, az);
ppp = Kakezan(rrr, ppp);
ppp = Kakezan(ppp, qqq);
cout << "\nAnser X = " << ppp.x
<< "\n Y = " << ppp.y
<< "\n Z = " << ppp.z << endl;
}
return 0;
}
http://staff.aist.go.jp/toru-nakata/quaternion.html
http://bbs.gameres.com/showthread.asp?threadid=73511
在gameres上看到的,感觉很创意。。。
实现方法
准备两个摄像机,对准同一点,交替渲染红和绿的画面,带上红绿眼镜 即可观察到4D的场景了!
即可观察到4D的场景了!
大家可以看看那这里,有源代码(C++&D3d实现的)
http://bbs.gameres.com/showthread.asp?threadid=73818

一个4D的例子
这周六数学竞赛,周日物理竞赛。
感觉暑假后对那些冲量矩啊,角动量啊,惠斯通电桥啊,无线网格啊,的感觉都好模糊了。。。
不过,个人认为重在享受这个过程,有没有拿到省一等奖是次要的。
祝自己好运。。。