之前一篇KMP讲的是直接的应用,这一篇将借助两道相似的POJ题目对next数组进行深入一些的讨论。
两道题目分别是:
POJ 1961 2406,题意是给出一个串s,找出这个能表示成某个字串A的K次联接,即s=[A...A] (K个A),要求K最大,即A最小。
暴力可以过2406,但1961没法过,超时。
看了discuss的讨论,只要计算KMP算法中的next数组,判断n (串长)能否被d = n-1-next[n-1] (即最后一个next)整除,若能,则s是s[next[n-1]...n-1]的n/d联接。具体细节没有证明。
下面给出我的一些想法,为什么以上判断是正确的。
首先,若s可以表示成[A...A],则next数组确实是符合以上整除的要求的,且从0到next[n-1]这个proper prefix (见上一篇KMP文章的定义)是s的最长的proper suffix。
其次,为什么d整除n,就能断定s是s[next[n-1]+1...n-1]的n/d次联接呢?
1) 用文字表述太麻烦,用下图说明
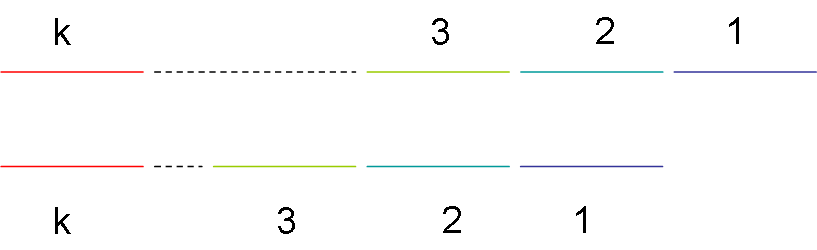
图中颜色一致的段是一样的(这是因为下面那段是上面那段的proper prefix),即上面的1等于下面的1,而由于下面的段是上面段的proper prefix,因此下面的1又等于上面的2,所以上面的1跟2是相等的。以此类推,上面的小段都是相等的。