glColor3f(0.3f, 0.9f, 0.0f);
for(int z = 0; z < _terrain->length() - 1; z++) {
//Makes OpenGL draw a triangle at every three consecutive vertices
glBegin(GL_TRIANGLE_STRIP);
for(int x = 0; x < _terrain->width(); x++) {
Vec3f normal = _terrain->getNormal(x, z);
glNormal3f(normal[0], normal[1], normal[2]);
glVertex3f(x, _terrain->getHeight(x, z), z);
normal = _terrain->getNormal(x, z + 1);
glNormal3f(normal[0], normal[1], normal[2]);
glVertex3f(x, _terrain->getHeight(x, z + 1), z + 1);
}
glEnd();
}
这里绘制地形。GL_TRIANGLE_STRIP是个新参数,它使OpenGL在每三个连续的顶点之间绘制一个三角形。如果你的顶点是v1,v2,v3...那么OpenGL会绘制三角形(v1,v2,v3),(v2,v3,v4),(v3,v4,v5),...为了绘制地形,对于每个z,我们以顶点(0,h1,z),(0,h2,z+1),(1,h3,z),(1,h4,z+1),(2,h5,z),(2,h6,z+1),...画三角形。使用triangle strips不仅比使用三角形更方便,速度也更快,由于发送给显卡的3D顶点更少了。我们的地形将像下面这样绘制:

我们绘制地形的这种方法,每个x-z平面网格点单元被向右外方的对角线分割为两个三角形。我们可以使用其他的分割线来分割每个单元,但如果我们的地形足够平滑,这变化并不大。我们也可以使用GL_QUADS来代替三角形,但当这个顶点不在同一平面上的时候这不是一个好的方法。
int main(int argc, char** argv) {
//...
_terrain = loadTerrain("heightmap.bmp", 20);
//...
} 在我们的main函数中,调用loadTerrain函数加载3D地形。
现在我们回头看看如何计算法向量。
//Computes the normals, if they haven't been computed yet
void computeNormals() {
if (computedNormals) {
return;
}
Vec3f** normals2 = new Vec3f*[l];
for(int i = 0; i < l; i++) {
normals2[i] = new Vec3f[w];
}
for(int z = 0; z < l; z++) {
for(int x = 0; x < w; x++) {
Vec3f sum(0.0f, 0.0f, 0.0f);
Vec3f out;
if (z > 0) {
out = Vec3f(0.0f, hs[z - 1][x] - hs[z][x], -1.0f);
}
Vec3f in;
if (z < l - 1) {
in = Vec3f(0.0f, hs[z + 1][x] - hs[z][x], 1.0f);
}
Vec3f left;
if (x > 0) {
left = Vec3f(-1.0f, hs[z][x - 1] - hs[z][x], 0.0f);
}
Vec3f right;
if (x < w - 1) {
right = Vec3f(1.0f, hs[z][x + 1] - hs[z][x], 0.0f);
}
if (x > 0 && z > 0) {
sum += out.cross(left).normalize();
}
if (x > 0 && z < l - 1) {
sum += left.cross(in).normalize();
}
if (x < w - 1 && z < l - 1) {
sum += in.cross(right).normalize();
}
if (x < w - 1 && z > 0) {
sum += right.cross(out).normalize();
}
normals2[z][x] = sum;
}
}
首先我们计算近似法向量,并保存在normals2变量中。估计给定点法向量的一种方法是取由这个点同相邻两个点组成的三角形的垂线。比如,三角形的顶点为这个点,这个点右边的点和这个外面的一个点,然后去这个三角形的垂线。
找到一个三角形的垂线,我们计算两个边的差乘。我们计算每个点的左右,里外四个边,然后计算一对边的差积决定一个三角形的垂直向量。对于每个顶点我们计算相邻的4个三角形的法向量并取均值(在和中正好成比例)。
几何上来说,4个法向量的均值究竟有什么意义?其实没有什么意义,只是我想出来的近似法向量的一种方法。计算机图形学主要原则是要看起来正确,因此来看看这种怪异的均值最后是否能工作。
注意必须对边缘的点使用一个if判断分支,因为他们没有4个相邻的三角形。
好了,我们计算一系列法向量。但是如果能将其平滑就更好了,这样每个法向量和其相邻的法向量就更加相似了。这样,我们3D场景的光照会更加平滑。对于只是用64个不同高度值的高度图特别重要,每个高度值都有精度问题,使光照看上去很粗糙。对了激励我们,这里是非平滑和平滑的法向量的对比图:
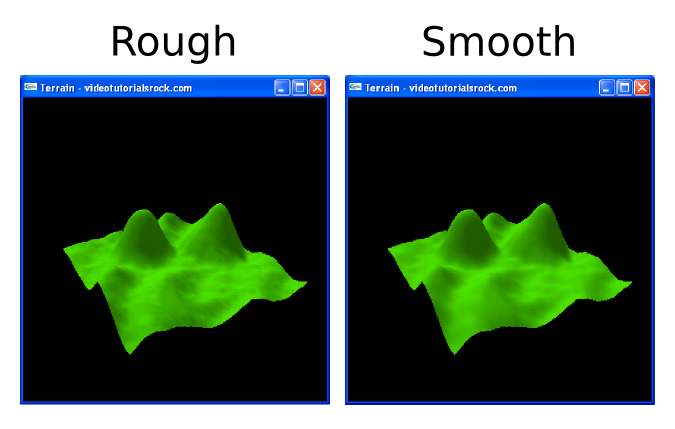
要怎样能平滑法向量呢?对于每个法向量,我们将其同周围的法向量做些平均。
const float FALLOUT_RATIO = 0.5f;
for(int z = 0; z < l; z++) {
for(int x = 0; x < w; x++) {
Vec3f sum = normals2[z][x];
if (x > 0) {
sum += normals2[z][x - 1] * FALLOUT_RATIO;
}
if (x < w - 1) {
sum += normals2[z][x + 1] * FALLOUT_RATIO;
}
if (z > 0) {
sum += normals2[z - 1][x] * FALLOUT_RATIO;
}
if (z < 0) {
sum += normals2[z + 1][x];
}
if (sum.magnitude() == 0) {
sum = Vec3f(0.0f, 1.0f, 0.0f);
}
normals[z][x] = sum;
}
}
对于每个法向量,取这个点的粗略的法向量和相邻点的粗略的法向量然后加权取均值。相邻的法向量权重为0.5,当前点的权重为1。这里的平均没有什么实际意义,但让场景好看。如果平均结果为0就指定一个任意向量。因为我们无法使用0向量(无法归一化),但有必须使用些什么。
我们场景里的光照看起来好极了。现在你了解了如何创建一个好看的3D地形啦!