基本方法的代码
好了,现在来看代码。警告:这些代码比前几棵的代码要复杂许多。在看8叉树的代码之前来看下其他的代码。
在include的声明之后,定义randomFloat函数,返回一个随机[0, 1)的float。
//Stores information regarding a ball
struct Ball {
Vec3f v; //Velocity
Vec3f pos; //Position
float r; //Radius
Vec3f color;
};
定义球的结构,有速度、位置、半径和颜色。速度表示在每个方向的移动速度。比如,速度(3, -2, 5)表示每秒沿着x的正半轴3个单位,向下每秒2个单位,负z轴方向每秒5个单位。
enum Wall {WALL_LEFT, WALL_RIGHT, WALL_FAR, WALL_NEAR, WALL_TOP, WALL_BOTTOM};
六面墙使用枚举型表示。
//Stores a pair of balls
struct BallPair {
Ball* ball1;
Ball* ball2;
};
//Stores a ball and a wall
struct BallWallPair {
Ball* ball;
Wall wall;
};
使用两个结构表示球-球和球-墙对,这样来表示潜在的碰撞。注意目前我忽略了球-墙碰撞。因为他们比球-球碰撞要简单许多,因此没有必要对其进行优化。不用担心,我们会处理的。
//Puts potential ball-ball collisions in potentialCollisions. It must return
//all actual collisions, but it need not return only actual collisions.
void potentialBallBallCollisions(vector<BallPair> &potentialCollisions,
vector<Ball*> &balls, Octree* octree) {
//Fast method
octree->potentialBallBallCollisions(potentialCollisions);
/*
//Slow method
for(unsigned int i = 0; i < balls.size(); i++) {
for(unsigned int j = i + 1; j < balls.size(); j++) {
BallPair bp;
bp.ball1 = balls[i];
bp.ball2 = balls[j];
potentialCollisions.push_back(bp);
}
}
*/
}
//Puts potential ball-wall collisions in potentialCollisions. It must return
//all actual collisions, but it need not return only actual collisions.
void potentialBallWallCollisions(vector<BallWallPair> &potentialCollisions,
vector<Ball*> &balls, Octree* octree) {
//Fast method
octree->potentialBallWallCollisions(potentialCollisions);
/*
//Slow method
Wall walls[] =
{WALL_LEFT, WALL_RIGHT, WALL_FAR, WALL_NEAR, WALL_TOP, WALL_BOTTOM};
for(unsigned int i = 0; i < balls.size(); i++) {
for(int j = 0; j < 6; j++) {
BallWallPair bwp;
bwp.ball = balls[i];
bwp.wall = walls[j];
potentialCollisions.push_back(bwp);
}
}
*/
}
在这些函数中,我们计算所有可能的球-球和球-墙碰撞,并加入到c++的vector容器中。他们仅仅向八叉树询问潜在的碰撞。如我所说,在说明了我们程序的基本机制之后再来看八叉树的工作机制。
如果你还不熟悉vector,那你可以将其看为一个变长的数组。你需要#include <vector>来使用它。通过调用vec.push_back(element)来在末尾添加元素。你可以通过vec[n]来访问和修改第(n+1)个元素,就像数组一样。你可以调用vec.size()来获取数组的大小。还有许多其他方法。(It slices, it dices, it does your homework and makes you breakfast.)声明一个BallPiars的数组如下vector<BallPair>。
接下来是moveBalls函数,它将所有的球移动速度*dt距离,使得在一个小的时间段里移动这些。然后是applyGreavity函数,在每个TIME_BETWEEN_UPDATES秒里调用。添加重力因素的做法是减少y轴的坐标,减少的值为y轴的速度*GRAVITY*TIME_BETWEEN_UPDATES。在现实生活中重力和这个类似,地球在y轴以每秒9.8m的速度使一个物体下降。
//Returns whether two balls are colliding
bool testBallBallCollision(Ball* b1, Ball* b2) {
//Check whether the balls are close enough
float r = b1->r + b2->r;
if ((b1->pos - b2->pos).magnitudeSquared() < r * r) {
//Check whether the balls are moving toward each other
Vec3f netVelocity = b1->v - b2->v;
Vec3f displacement = b1->pos - b2->pos;
return netVelocity.dot(displacement) < 0;
}
else
return false;
}
这个函数检测两个球目前是否相撞。 If (b1->pos - b2->pos).magnitudeSquared() < r * r不为真意味这两个球的距离比半径和要大,然后就可以知道他们没有相撞。否则检查两个球是否相向运动,如果他们向反方向运动,则很有可能刚刚撞击完,他们不会再相撞。
//Handles all ball-ball collisions
void handleBallBallCollisions(vector<Ball*> &balls, Octree* octree) {
vector<BallPair> bps;
potentialBallBallCollisions(bps, balls, octree);
for(unsigned int i = 0; i < bps.size(); i++) {
BallPair bp = bps[i];
Ball* b1 = bp.ball1;
Ball* b2 = bp.ball2;
if (testBallBallCollision(b1, b2)) {
//Make the balls reflect off of each other
Vec3f displacement = (b1->pos - b2->pos).normalize();
b1->v -= 2 * displacement * b1->v.dot(displacement);
b2->v -= 2 * displacement * b2->v.dot(displacement);
}
}
}
handleBallBallCollisions 使所有正在相撞的球相互弹开。首先,调用potentialBallBallCollisions 找到可能的碰撞。然后遍历所有的潜在碰撞对找到那一对是真的碰撞了。对于每个碰撞,通过将速度取反,方向为一个球心到另一个球心,让球相互弹开。下面的图显示如何计算碰撞之后小球的速度:
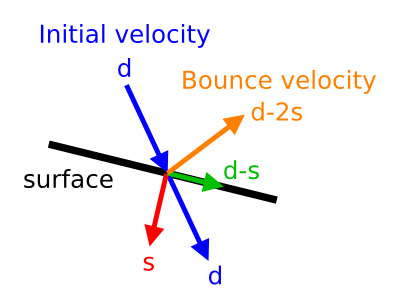
图中,d是小球初始的速度;s是球球方向上的投影;d-2s是弹开之后的速度。为了确定s,我们计算第二个球到第一个球的方向(b1->pos - b2->pos).normalize()。然后点乘初始速度,得到s。由于小球在弹开之后的速度没有下降,小球会永远碰撞下去。
testBallWallCollision 函数返回一个特定的球和给定的墙是否碰撞。同理,我们确保球是向着墙运动的以保证他们正在相撞。
//Handles all ball-wall collisions
void handleBallWallCollisions(vector<Ball*> &balls, Octree* octree) {
vector<BallWallPair> bwps;
potentialBallWallCollisions(bwps, balls, octree);
for(unsigned int i = 0; i < bwps.size(); i++) {
BallWallPair bwp = bwps[i];
Ball* b = bwp.ball;
Wall w = bwp.wall;
if (testBallWallCollision(b, w)) {
//Make the ball reflect off of the wall
Vec3f dir = (wallDirection(w)).normalize();
b->v -= 2 * dir * b->v.dot(dir);
}
}
}
这个函数使所有和墙相撞的球弹开。和handleBallBallCollisions类似,我们计算潜在的球-墙碰撞,遍历并找出实际的球-墙碰撞,然后让球弹开。我们通过将和墙垂直方向的速度取反实现弹开。
//Applies gravity and handles all collisions. Should be called every
//TIME_BETWEEN_UPDATES seconds.
void performUpdate(vector<Ball*> &balls, Octree* octree) {
applyGravity(balls);
handleBallBallCollisions(balls, octree);
handleBallWallCollisions(balls, octree);
}
现在将applyGravity, handleBallBallCollisions和handleBallWallCollisions放入performUpdate函数中,这个函数我们每个TIME_BETWEEN_UPDATES秒都要调用。
vector<Ball*> _balls; //All of the balls in play
float _angle = 0.0f; //The camera angle
Octree* _octree; //An octree with all af the balls
//The amount of time until performUpdate should be called
float _timeUntilUpdate = 0;
GLuint _textureId;
这是我们所有的全局变量。全局变量通常是糟糕的设计,因为理解全局变量,你可能要将整个main.cpp放在脑袋中。全局变量会通过令人迷惑的改变值或者在小的作用域中容易滥用。有比全局变量更好的解决方案,但这里不用因为我不想将注意力从碰撞检测转移。相反,我们假设这些不是全局变量,他们只能通过最顶层的函数访问,这些顶层的函数为initRendering, drawScene, handleKeypress, handleResize还有一个称之为cleanup的函数。为了使这些变量突出,使他们都以下划线开头。(另外,在c++中,变量不能以两个下划线开头或者一个下划线跟着一个大写字母。)
//Deletes everything. This should be called when exiting the program.
void cleanup() {
for(unsigned int i = 0; i < _balls.size(); i++) {
delete _balls[i];
}
delete _octree;
}
当我们退出程序,需要确保删除了所有的球和8叉树。