一:BF算法
如果让你写字符串的模式匹配,你可能会很快的写出朴素的bf算法,至少问题是解决了,我想大家很清楚的知道它的时间复杂度为O(MN),原因很简单,主串和模式串失配的时候,我们总是将模式串的第一位与主串的下一个字符进行比较,所以复杂度高在主串每次失配的时候都要回溯,图我就省略了。
二:KMP算法
刚才我们也说了,主串每次都要回溯,从而提高了时间复杂度,那么能不能在“主串”和“模式串”失配的情况下,主串不回溯呢?而是让”模式串“向右滑动一定的距离,对上号后继续进行下一轮的匹配,从而做到时间复杂度为O(M+N)呢?所以kmp算法就是用来处理这件事情的。
代码:
#pragma once
#include <iostream>
// --- 朴素匹配算法 ---
int NaiveMatch(const char * txt, const char * pat)
{
int nTxtLength = strlen(txt);
int nPatLength = strlen(pat);
int nTxt = 0;
int nPat = 0;
int nCount = 0; // 计数
while (nTxt <= nTxtLength - nPatLength && nPat < nPatLength)
{
++nCount;
if (pat[nPat] == txt[nTxt+nPat])
{
++nPat;
}
else
{
++nTxt;
nPat = 0;
}
}
std::cout << "NaiveMatch, compare counts: " << nCount << std::endl;
return (nPat == nPatLength ? nTxt : -1);
}
// --- KMP 匹配算法 ---
void GetNext(const char* pattern, int next[])
{
next[0] = 0;
int j = 0;
for (int i = 1; i < strlen(pattern); i++)
{
while( j > 0 && pattern[j] != pattern[i] )
{
j = next[j-1];
}
if (pattern[j] == pattern[i])
j++;
next[i] = j;
}
}
int KMPMatch(const char* src, const char* pattern, int next[])
{
int nSrc = 0;
int nPattern = 0;
int nCount = 0; // 计数
while(nSrc < strlen(src) && nPattern < strlen(pattern))
{
++nCount;
if (0 == nPattern || src[nSrc] == pattern[nPattern])
{
++nPattern;
++nSrc;
}
else
{
nPattern = next[nPattern];
}
}
std::cout << "KMP, compare counts: " << nCount << std::endl;
return (nPattern == strlen(pattern) ? nSrc - nPattern : -1);
}
#define PRINT_RESLUT(v) { if(-1 == (v)) std::cout << "No Find!"; else std::cout << "Position = " << (v); std::cout << std::endl << std::endl; }
int main()
{
const char* Src = "abc1aabc1aabc1aaababc1aababc1aabc1aaabc1aabc1aababc1aaabaabcbc1aa";
const char* Pattern = "abaabc";
int nPos = -1; // 保存匹配到的位置
/// 朴素匹配算法
nPos = NaiveMatch(Src, Pattern);
PRINT_RESLUT(nPos);
/// KMP匹配算法
int next[6] = {0};
GetNext(Pattern, next);
nPos = KMPMatch(Src, Pattern, next);
PRINT_RESLUT(nPos);
system("pause");
return 0;
}
运行结果:
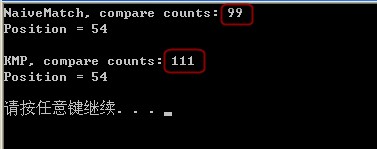
疑惑:为什么KMP的效率会更低?
