|
|
1.20
下面用 % 表示过程 remainder,那么正则序的过程如下:
(gcd 206 40)
(if (= 40 0) 206 (gcd 40 (% 206 40)))
(gcd 40 (% 206 40))
(if (= (% 206 40) 0) ;<## 1> [6]
40
(gcd (% 206 40) (% 40 (% 206 40))
(gcd (% 206 40) (% 40 (% 206 40)))
(if (= (% 40 (% 206 40)) 0) ;<## 2> [4]
(% 206 40)
(gcd (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))))
(gcd (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))
(if (= (% (% 206 40) (% 40 (% 206 40))) 0) ;<## 4>[2]
(% 40 (% 206 40))
(gcd (% (% 206 40) (% 40 (% 206 40)))
(% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))))
(gcd (% (% 206 40) (% 40 (% 206 40)))
(% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))))
(if (= (% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))) 0) ;<## 7>[0]
(% (% 206 40) (% 40 (% 206 40)))
(gcd ...)
(% (% 206 40) (% 40 (% 206 40))) ;<## 4>[2]
可以看出需要调用 remainder 共 1+2+4+7+4 = 18 次。
应用序计算过程如下:
(gcd 206 40)
(if (= 40 0) 206 (gcd 40 (% 206 40))) ;<##>
(gcd 40 6)
(if (= 6 0) 40 (gcd 6 (% 40 6))) ;<##>
(gcd 6 4)
(if (= 4 0) 6 (gcd 4 (% 6 4))) ;<##>
(gcd 4 2)
(if (= 2 0) 4 (gcd 2 (% 4 2))) ;<##>
(gcd 2 0)
(if (= 0 0) 2 (gcd 0 (% 2 0)))
2
可以看出共需 4 次。
1.16
(define (fast-expt x n)
(fast-expt-iter x n 1))
(define (fast-expt-iter x n a)
(cond ((= n 0) a)
((even? n) (fast-expt-iter (square x)
(/ n 2)
a))
(else (fast-expt-iter x
(- n 1)
(* a x)))))
1.17
(define (multi x y)
(if (= y 0)
0
(+ x (multi x (- y 1)))))
(define (fast-multi x y)
(cond ((= y 0) 0)
((even? y) (double (fast-multi x
(half y))))
(else (+ x (fast-multi x (- y 1))))))
(define (double x) (+ x x))
(define (half y) (/ y 2))
1.18
(define (double x) (+ x x))
(define (half y) (/ y 2))
(define (fast-multi x y)
(fast-multi-iter x y 0))
(define (fast-multi-iter x y p)
(cond ((= y 0) p)
((even? y) (fast-multi-iter (double x)
(half y)
p))
(else (fast-multi-iter x (- y 1) (+ p x)))))
1.19
;T(pq):(a,b)=>(bq+aq+ap, bp+aq)
;T(pq):(bq+aq+ap, bp+aq)=>((bp+aq)q + (bq+aq+ap)q + (bq+aq+ap)p,
; (bp+aq)p + (bq+aq+ap)q)
; => (2bpq+2aqq+bqq+2apq+app, bpp+2apq+bqq+aqq)
; => (b(2pq+qq)+a(2pq+qq)+a(qq+pp), b(qq+pp)+a(2pq+qq))
;q' = 2pq+qq
;p' = qq+pp
;
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(fib-iter a
b
(+ (* p p) (* q q))
(+ (* 2 p q ) (* q q))
(/ count 2)))
(else (fib-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- count 1)))))
1.14
计算过程的树如下:
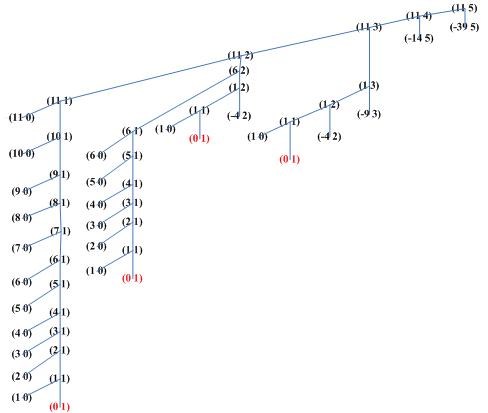
很容易看出,计算过程的空间需求,也就是树的深度,取决于最左边的子树,即(n 1),它的深度是n+6,O(n).
然后对于计算步数,也就是树的节点数,我们知道对于一个二叉树,树的节点数 = 左子树节点数 + 右子树节点数 + 1.
先来看 (n 1) 子树,设它的节点数是f(n), 而且总有,非叶节点左子树节点数为1
当 n=1,f(1) = 3
n>1, f(n) = 1 + f(n-1) + 1 = f(n-1) + 2 = f(n-2) + 2*2
= f(n-(n-1)) + 2*(n-1) = 2n + 1
= O(n)
再来看 (n 2) 子树,设它的节点数 g(n), 设 ┌ n/5 ┐ = A
g(n) = f(n) + g(n-5) + 1 = f(n) + f(n-5) + g(n-5*2) + 2
= f(n) + ... + f(n-5*(A-1)) + g(n-5*A) + 2A
= O(n^2)
依此类推,可以得出结论 (n 5) 的计算步数增长的阶 为 O(n^5)
1.15
a) 12.15 连除 5次 3 小于 0.1 ,所以是 5次
b) 可以看出每调用一次 p 过程,需要递归1次 sine ,空间加1,计算步数加2,关键是p的次数:
对于a,调用次数t,那么 a*3^(-t) < 0.1 , 即 10a < 3^t ==> lg(10a)/lg3 < t,
所以增长阶 空间和时间 都为 O(log a)
我为什么推荐 SICP?
向大家推荐 SICP,不知道有多少人看了,也不知道有多少人明白了,更不知道有多少人惊叹了。或者你根本不屑一顾,或者你看见 Lisp 那层层括号心生畏惧,又或者你了了一瞥,觉得没什么精彩之处。那我真的很失望。
我为什么要推荐SICP,而且为什么如此执着?这本不算厚的书带给我的观念,是从未有过的,是关乎于软件本质的。曾几何时,我觉得我看到了计算机编程书中没有的哲学观,但这一次我的梦破灭了,那些已经被写进书里差不多快 30 年了。
对于 SICP,我真正算看完的,恐怕只有第一章。我现在就来谈谈我的心得,以再次向你展现这本书的魔力。
第一章作为基础,作者并没有象后续章节写太多的软件思想,主要还是介绍 Scheme 语言,所以草草看去,没什么精辟之处。不过在第一章中,作者用了大量的篇幅来探讨数学问题,因为他想向你揭示程序设计中的核心哲学:抽象。而数学无疑是最好的例子。
了解数学史的人,应该知道整个数学史,就是一个不断抽象的历史。古希腊人将字母引入计算,使数学不再只是算术,而且具有表达抽象规则的能力。近代数学对函数和微积分的探求中,用 f(x) 替代了多项式表达式,函数更一般了,然后 n 维空间、复分析、映射、泛函,抽象代数、群论,等等等等,直到集合论,摧毁了数学的基石,使数学界再次陷入沉思。
构造程序的方法也是抽象。从最简单的元素开始,基本元素(自演算表达式,包括数字,字符串和布尔值),然后定义基本过程(基本运算符,四则运算和布尔运算),进一步,自定义标识符(如同代数),再自定义过程(函数),再将过程作为值参与运算(高阶过程)。一步步的抽象,形成了整个程序的结构。而我们编程,无非就是从现实世界抽象出模型,再将模型不断的提炼抽象,属性、方法、类、继承、层次、框架。
编程就是一个不断抽象的过程。我再次把作者在第一章末写下的结论抄在这里,作为最后的注脚。
“作为编程者,我们应该对这类可能性保持高度敏感,设法从中设别出程序中的基本抽象,基于它们去进一步构造,并推广它们以创建威力更强大的抽象。当然,这并不是说总应该采用尽可能抽象的方式去写程序,程序设计专家们知道如何根据工作中的情况,去选择合适的抽象层次。但是,能基于这种抽象去思考确实是最重要的,只有这样才可能在新的上下文中去应用它们。高阶过程的重要性,就在于我们能显式地用程序设计语言的要素去描述这些抽象,使我们能像操作其他计算元素一样去操作它们。”
1.11
递归计算过程为
(define func-recu
(lambda(n)
(cond ((< n 3) n)
(else (+ (func-recu (- n 1))
(* 2 (func-recu (- n 2)))
(* 3 (func-recu (- n 3))))))))
迭代计算过程为
(define func-iter
(lambda(a b c n)
(if (= n 0)
a
(func-iter b c (+ (* 3 a) (* 2 b) c) (- n 1)))))
(define (func n) (func-iter 0 1 2 n))
1.12
中文版原题翻译有误,应为计算pascal三角中的元素。
;pas(n,k)
;if (k=1) or (k=n), then pas(n,k) = 1
;else pas(n,k) = pas(n-1,k-1) + pas(n-1,k)
(define pas (lambda(n k)
(if (or (= k 1) (= k n))
1
(+ (pas (- n 1) (- k 1))
(pas (- n 1) k)))))
1.13
中文版原题翻译遗漏 提示 :ψ=(1-√5)/2
已知,φ^2 = φ + 1, 那么 φ^n = φ^(n-1) + φ^(n-2)
同理,ψ^2 = ψ + 1, 那么 ψ^n = ψ^(n-1) + ψ^(n-2)
又 φ-ψ = (1+√5)/2 - (1-√5)/2 = √5
when n=0, Fib(0) = 0 = (φ^0-ψ^0)/√5
when n=1, Fib(1) = 1 = √5/√5 = (φ-ψ)/√5
when n>2, Fib(n) = Fib(n-1) + Fib(n-2) = (φ^(n-1)-ψ^(n-1))/√5 + (φ^(n-2)-ψ^(n-2))/√5
= ((φ^(n-1)+(φ^(n-2))) - (ψ^(n-1)+ψ^(n-2)))/√5
= (φ^n - ψ^n)/√5
又 -1< ψ < 0, 故 -0.5< -1/√5< ψ^n/√5 < 1/√5 <0.5
, 而 φ^n/√5 = ψ^n/√5 + Fib(n)
可知 |φ^n/√5 - Fib(n)| < 0.5, Fib(n)是最接近φ^n/√5的整数。
首先,可以写出这个函数的函数式:
0, y = 0;
f(x,y) = 2y, x = 0;
2, y = 1;
f(x-1, f(x, y-1));
那么,对于 f(0,n), n>=0
当 n >= 1 时, f(0,n) = 2n ,
而当 n = 0 时, f(0,0) = 0 = 2*0, 也满足 2n ,
故 f(0,n) = 2n, n>=0.
对于f(1,n), n>=1
当 n > 1 时,有 f(1,n) = f(0, f(1, n-1)) = 2*f(1,n-1),
设 f(1,n) = 2^n
if n = 1, f(1,1) = 2 = 2^1
when n > 1, if f(1,n-1) = 2^(n-1)
then f(1,n) = 2*f(1,n-1) = 2*(2^(n-1)) = 2^n
故 f(1,n) = 2^n, n>0.
对于f(2,n), n>0
if n > 1 ,then f(2,n) = f(1, f(2, n-1)) = 2^f(2,n-1),
设 f(2,n) = 2^(2^(... (n 个 2)
if n = 1, then f(2,1) = 2
when n > 1, if f(2, n-1) = 2^(2^(... (n-1)
then f(2,n) = 2^f(2,n-1) = 2^(2^(
这样我们对于 (A 1 10) = 2^10 = 1024, (A 2 4) = 2^(2^(2^2)) = 2^16 = 65536
而 (A 3 3) = (A 2 A(3 2)) = A(2 A(2 A(2 1))) = (A 2 4) = 2^16 = 65536
(f n) = (A 0 n) = 2n
(g n) = (A 1 n) = 2^n
(h n) = (A 2 n) = 2^(2^(... (n个2)
---------------------------------------------
在网上可以找到关于 Ackermann 函数的讨论,主要是针对这个双递归如何用迭代来实现,Ackermann 函数是 德国数学家W.Ackermann 在1928年提出的。在 WikiPedia 英文版上可以搜索 Ackermann function
词条,有详细介绍,不过这个Ackermann function
略有不同。如下图:
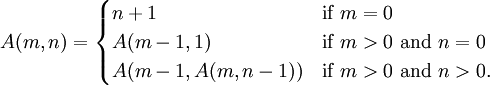
很显然,第一个是递归的,第二个是迭代的。
(+ 4 5)
(if (= 4 0) 5 (inc (+ (dec 4) 5)))
(inc (+ 3 5))
(inc (if (= 3 0) 5 (inc (+ 2 5))))
(inc (inc (if (= 2 0) 5 (inc (+ 1 5)))))
(inc (inc (inc (if (= 1 0) 5 (inc (+ 0 5))))))
(inc (inc (inc (inc (if (= 0 0) 5 (inc (+ (dec 0) 5)))))))
(inc (inc (inc (inc 5))))
(inc (inc (inc 6)))
(inc (inc 7))
(inc 8)
9
(+ 4 5)
(if (= 4 0) 5 (+ 3 6))
(if (= 3 0) 6 (+ 2 7))
(if (= 2 0) 7 (+ 1 8))
(if (= 1 0) 8 (+ 0 9))
(if (= 0 0) 9 (+ (dec 0) (inc 9)))
9
采用1.7中的变化率为终止检测。
(define (cube-root x)
(cube-root-iter x 1.0 x))
(define (cube-root-iter last-guess guess x)
(if (enuf? last-guess guess)
guess
(cube-root-iter guess (improve guess x) x)))
(define (enuf? x y)
(< (/ (abs (- x y)) y) 0.001))
(define improve (lambda (y x)
(/ (+ (/ x (* y y)) (* 2 y)) 3)))
目前为止,程序的表现形式是对过程的叙述,顺序、分支、循环结构是最基本的原子形式。而面向过程的分析和设计无疑是最自然的框架结构,它将过程形式的代码段再次迭代的以过程形式组合,形成整个程序。就像将句子连成段,将段连成章,将章连成篇,将篇连成书。这也是最符合阅读者思维的形式,整个程序就像一个内含超链接的文本小说,主体上是流畅的,符合连续思维的。
面向对象程序不能说是颠覆性改变,它的原子表现形式仍然是顺序、分支和循环。而由于依赖于过程性系统的装载,其整体的最外层仍然是一个过程性的函数。它与面向过程在其表现形式上的不同,仅仅存在于中间层。
面向对象程序的表现形式是词条式的,至少是传记体的,而不是编年史。你可以想象,一部小说,作者首先把所有的故事按照角色重新归类,再分割为一个个小故事,可以想象是这样的:
——传记式:
《张三传》
张三,秦人,少年,虬髯黑脸,为人仗义。
逸事一:若傍晚时访之,必留宿,夜必邀相饮。三十三年春,李四自华阴来,……
《李四传》
李四,中原人,白脸壮年书生,十六岁举秀才。
逸事一:其人好游,某年遇张三……
——词条式:
醉酒: 张三与李四饮酒,大醉……
举秀才: 李四,十六时……
张三其人: 秦人,少年,虬髯黑脸,为人仗义……
巧遇: 三十三年,李四巧遇张三……
仗义好客: 张三好客,若傍晚时访之,必留宿,夜必邀相饮……
这种表现形式是某种词条式的分裂,故事被不断的片段化,一个比较好的面向对象程序一般会有大量的细粒度对象,对象的属性和方法都不多,方法都很短。虽然这种表现形式能解决一些过程性叙述的不足,但无疑过分的碎片化会带来理解上困难,传记式尚好,词条式就很难了。这就是面向对象程序在形式上出现的弱点。分析设计时,需时时脑中回想整体结构,以防偏离。而阅读维护时,需要把这些片段慢慢织起来,连成一个故事。
----------------------------------------------
将SICP的注脚240记在这里:
对象模型对世界的近似在于将其分割为独立的片断,函数式模型则不是沿着对象间的边界去做模块化,当“对象”之间不共享的状态远远大于它们所共享的状态时,对象模型就特别好用。这种对象观点失效的一个地方就是量子力学,在那里,将物体看作独立的粒子就会导致悖论和混乱。将对象观点与函数式观点合并可能与程序设计的关系不大,而是与基本认识论有关的论题。
对于正文中的 good-enough? 谓词,设所求 x 的真实平方根为 xt,那么我们的依据是当 guess 从 1 趋向与 xt 的平方差 小于 c(0.001) 时,guess 近似于 xt。实际当 xt^2 也就是 x 足够小时, guess 会 逐渐稳定在 √c 附近。从下面实验可以看出:
> (sqrt (square 0.1))
0.10032578510960607
> (sqrt (square 0.05))
0.054237622808967656
> (sqrt (square 0.01))
0.03230844833048122
> (sqrt (square 0.005))
0.031515954454847304
> (sqrt (square 0.001))
0.031260655525445276
> (sqrt (square 0.0001))
0.03125010656242753
>
因为 guess^2 < c + x
, 当 x < c 时,guess 就更多的依赖于 c 了。
对于特别大的数,由于浮点数在特别大时,离散性非常明显,相邻的两个数之间的差距会非常大,导致 |guess^2 - x| 始终 大于 c,计算便进入了 无限循环。
比如计算 (sqrt 1e300)
使用变化率改进后的代码如下:
(define (sqrt-new x)
(sqrt-iter-new x 1.0 x))
(define (sqrt-iter-new s1 s2 x)
(if (enuf-new? s1 s2)
s2
(sqrt-iter-new s2 (improve s2 x) x)))
(define (enuf-new? s1 s2)
(< (/ (abs (- s1 s2)) s1) 0.001))
可以测算几个数,验证结果还是比较好的。
> (sqrt-new (square 1e150))
1.0000000000084744e+150
> (sqrt-new (square 1e-150))
1.0000000000084744e-150
|