一般仿射变换
3x3矩阵仅能表达3D中的线性变换,不能包含平移。经过4x4矩阵的武装后,现在我们可以构造包含平移在内的一般仿射变换矩阵了。例如:
(1)绕不通过原点的轴旋转。
(2)沿不穿过原点的平面缩放。
(3)沿不穿过原点的平面镜像。
(4)向不穿过原点的平面正交投影。
它们的基本思想是将变换的"中心点"平移到原点,接着进行线性变换,然后再将"中心点"平移回原来的位置。开始使用平移矩阵T将点P移到原点,接着用线性变换矩阵R进行线性变换,最终的仿射变换矩阵M等于矩阵的积,即:TRT-1。T-1是平移矩阵,执行和T相反的变换。
观察这种矩阵的一般形式,它非常有趣。让我们先用 "分块"形式写出前面用到的T、R、T-1。

可以看出,仿射变换中增加的平移部分仅仅改变了4x4矩阵的最后一行,并没有影响到上面所包含的线性变换的3x3部分。
透视投影
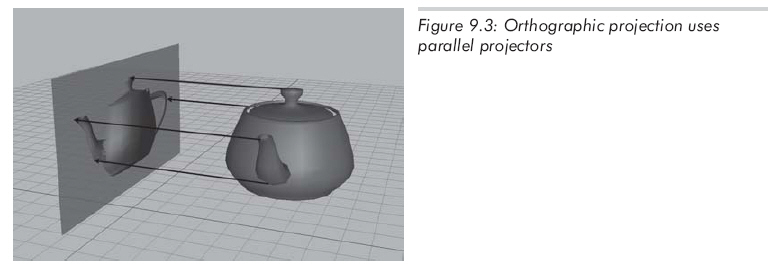
学习透视投影最好的方法是将它和平行投影相比较。正交投影也称作平行投影,因为投影线都是平行的(投影线是指从原空间中的点到投影点的连线)。正交投影中的平行线如图9.3所示:
3D中的透视投影仍然是投影到2D平面上,但是投影线不再平行,实际上,它们相交于一点,该点称作投影中心。如图9.4所示:
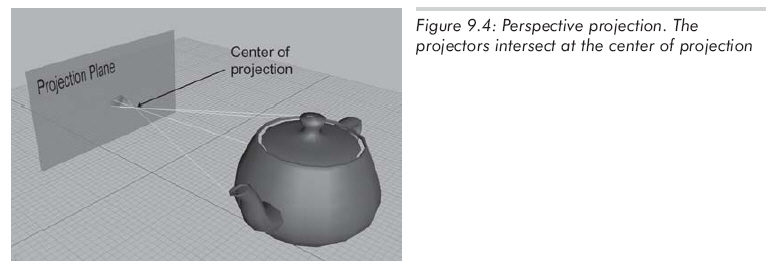
因为投影中心在投影平面前面,投影线到达平面之前已经相交,所以投影平面上的图像是翻转的。当物体远离投影中心时,正交投影仍保持不变,但透视投影变小了。如图9.5所示:

图9.5中,右边的茶壶离投影平面更远,所以它的投影比离投影平面较近的那个茶壶小。这是一种非常重要的视觉现象,称作透视缩略。
小孔成像
透视投影在图形学中非常重要,因为它是人类视觉系统的模型。实际上,人类视觉系统远比这复杂,因为我们有两只眼睛,而且对于每只眼睛,投影表面(视网膜)不是一个平面。所以,让我们来看一个简单些的例子----小孔成像。小孔成像系统就是一个盒子,一侧上有小孔,光线穿过小孔照射到另一侧的背面,那里就是投影平面。如图9.6所示:
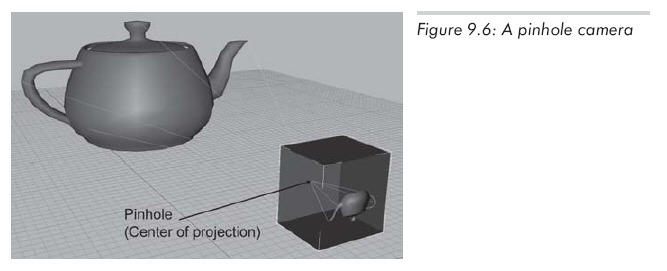
图9.6中,盒子左面和右面是透明的,以使你能看见盒子内部。注意盒子内部的投影是倒着的,这是因为光线(投影线)已经在小孔处(投影中心)相交了。
让我们探索小孔成像背后的几何原理。设想一个3D坐标系,它的原点在投影中心,z轴垂直于投影平面,x和y轴平行于投影平面。如图9.7所示:
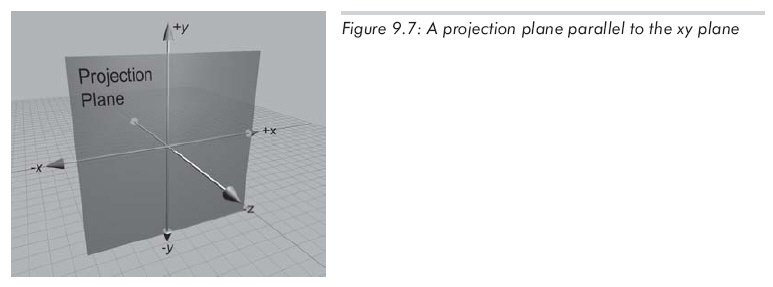
让我们看看能否计算出任意点p通过小孔投影到投影平面上的坐标p'。首先,需要知道小孔到投影平面的距离,设为d。因此,投影平面为z=-d。现在,从另一个角度来看问题,求出新的y。如图9.8所示。
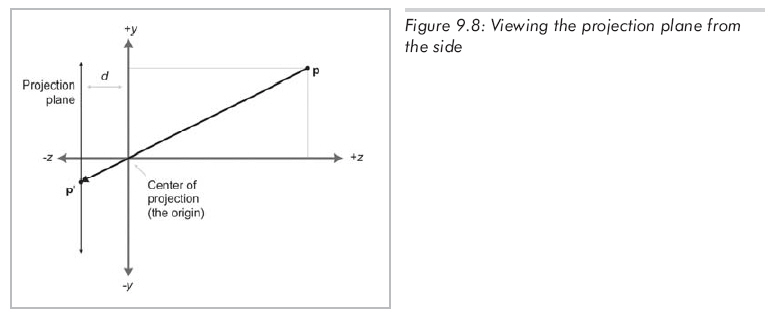
由相似三角形得到:
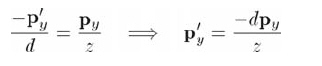
注意小孔成像颠倒了图像,py和py'的符号相反。px'的值可通过类似的方法求得:
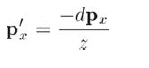
所有投影点的z值都是相同的:-d。因此,点p通过原点向平面z=-d投影的结果如公式9.11所示:
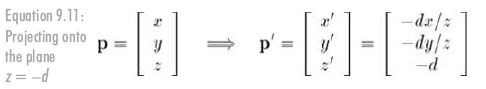
在实际应用中,负号会带来不必要的复杂性。所以将投影平面移到投影的前面(也就是说,平面z=d),如图 9.9所示:
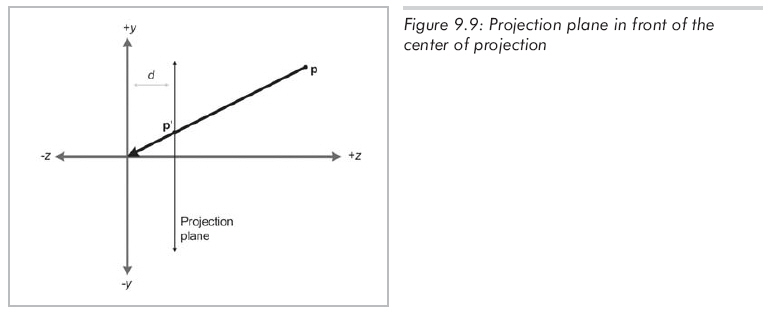
当然,这对于实际的小孔成像是不可能的。因为设置小孔的目的就是使光线只能通过小孔,但在计算机数学世界中,可以不理会这些规定。如你所愿,将投影平面移到投影中心前面,烦人的负号消失了,如公式9.12所示:
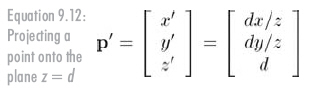
使用4x4矩阵进行透视投影
从4D到3D的变换就意味着除法运算,因此我们可以利用4x4阶矩阵来编写代码,以实现透视投影。基本思想是提出一个关于p'的公式,其中的x、y、z有公分母,然后构造一个4x4矩阵,使w与这个公分母相等。这里我们假设初始点处有w=1。
先对3D形式表达的p'公式变形,可以得到:
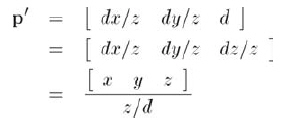
将4D齐次向量变换到3D时,要用4D向量除以w,反推可知p'的4D形式为:
[x y z z/d]
因此我们需要一个4x4矩阵,它可接收一个奇异的齐次向量。该向量的形式为[x, y, z, 1],然后将其变换为上述形式。这样的矩阵如公式9.13所示:

这样就得到了一个4x4投影矩阵,有几个需要注意的地方:
(1)乘以这个矩阵并没有进行实际的透视投影变换,它只是计算出合适的分母。投影实际发生在从4D向3D变换时。
(2)存在多种变换。例如,将投影平面放在z=0处而投影中心在[0, 0, -d],这将导致一个不同的公式。
(3)这里看起来比较复杂,似乎只需要简单地除以z,不必劳烦矩阵。那么为什么要使用齐次矩阵呢?第一,4x4矩阵提供了一个方法将投影表达为变换,这样就能和其他变换相连接;第二,使得投影到不平行于坐标轴的平面变得可行。实际上,我们不需要齐次坐标做任何运算,但4x4矩阵提供了一种简洁的方法表达和操纵投影变换。
(4)实际的图形几何管道中的投影矩阵不像这里导出的那样,还有许多重要的细节需要考虑。如用以上矩阵对向量进行变换后,z值实际上被舍弃了,而很多图形系统的z缓冲用到了该值。