eryar

B样条曲线比Bezier曲线更灵活，它的灵活性来自于你对基函数灵活地控制。我将对B样条的各组成部分进行讲解，首先讲一下控制顶点（Control Points）。

Control Points 控制顶点

Bezier曲线的控制顶点对整条曲线都有影响，即改变某一顶点的位置，对整条曲线都有影响，因而Bezier曲线不具有局部修改性。

由于灵活性的缘故，你可以对B样条设置任意数量的控制顶点，也可以确定各控制顶点的影响范围。

Degree and Order 次数和阶数

多项式曲线时，曲线的次数是由多项式中变量指数最高项确定。Bezier曲线时，曲线的次数由控制顶点数N确定，即N个控制顶点的曲线的次数是（N-1）次。基于这一点，我将引入一些新的术语来讨论曲线的次数和阶数，即阶数（Order）由设计值k确定，次数（Degree）则为（k-1）。

B样条把控制顶点数N与曲线的次数和控制顶点影响范围解耦。再抽象点说，曲线上的点只受一些控制顶点的影响，而不是任意控制顶点。或者说每个控制顶点只影响曲线上的一部分点的值。这就有意思啦，因为你对曲线有了局部修改的权力。你可用16个控制顶点定义一条曲线，但是它的阶数为4。如图4.1所示，移动一个控制顶点只会影响曲线上的一部分。若要用Bezier曲线来实现，就只能是把几个Bezier曲线拼接啦。

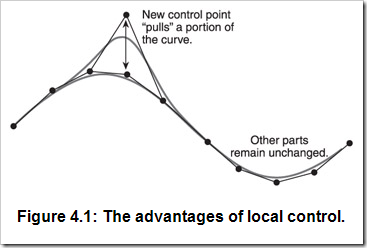
我已经讲到了术语阶数（Order）、次数（Degree），及控制顶点对曲线区间的影响，但是并没有讲到具体是怎样影响的。使用Bezier曲线时，没有任何的机制来限制影响的区间，因为任意一个控制顶点的改变都会影响到曲线上的每个点。B样条给你更多的控制，正是由于有节点向量（Knot Vectors）的机制。

Knot Vectors 节点向量

节点向量的目的就是描述控制顶点的影响范围。想象一下你想画一个有五个控制顶点的三阶曲线，每个控制顶点只会影响到参数区间上的曲线的一小部分。你可以描述任意一个控制顶点的影响范围为：[t₀, t₃], [t ₁, t₄], [t₂, t₅], [t₃, t₆], [t₄, t₇]。也可以在一个单一序列中紧凑的写成：[t₀ t₁ t₂ t₃ t₄ t₅ t₆ t₇]。这就是节点向量。图4.3所示为正式地表示了节点向量的影响范围：

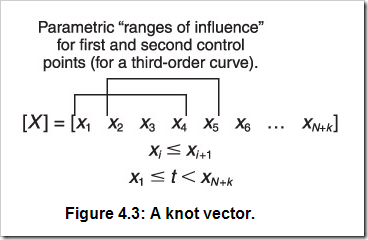
还可以从本例中推出几个更普遍的结论。首先，一个节点向量必须有N+k个元素；其次，节点向量必须是单调递增的。即每个节点向量的元素必须比前一个大或相等。单调递增的区间可以是任意的，当然也可以是[0，1]。下面是三个节点向量的例子。注意第二个节点向量和第三个在功能上相同，即用它们将会生成相同的曲线：

[X] = [3 4 5 6 7 8]

[X] = [1 2 3 4 5 6 7 8]

[X] = [0.125 0.25 0.375 0.5 0.625 0.75 0.875 1.0]

本书中大部分情况下将会使用整型的节点向量值，如第二种，因为这样解释起来要简单些。而在程序代码中，我将使用单位化后的节点向量，因为当参数区间为[0，1]时，考虑不同的范围要简单些。这两种情况产生的曲线没什么不同。

通常喜欢按节点向量是否均匀分布把节点向量分为均匀节点向量和非均匀节点向量。各举例如下：

• [X] = [1 2 3 4 5 6] (uniform)

• [X] = [1 3 5 7 9 11] (uniform)

• [X] = [1 2 2 3 3 4] (nonuniform)

• [X] = [1 2 3 3 4 5] (nonuniform)

节点向量还有两种类型：开放（Open）和周期性的（Periodic）。

至此为止，你已经知道创建B样条曲线的所有内容，除了B样条的基函数。知道一系列控制顶点可以用来定义曲线；知道可以用阶数及其相应的次数来描述曲线的属性；知道节点向量的机制，控制顶点是怎样来影响曲线的。你还需要一个基本的部分，即把上面所有组合在一起来画些东西，这就是基函数（the Basis Function）。

B样条基函数 B-Spline Basis Functions

在第三章讲Bezier曲线时，生活要简单的多。Bezier曲线的Bernstein基函数只是控制顶点的函数。现在，有了更多的灵活性，但是需要关注的就更多。（能力越大，责任越大。）除了控制顶点以外，B样条基函数还需要解释曲线的次数，还有由节点矢量定义的区间。这个基函数不是由Bernstein多项式定义的，而是由Cox-de Boor递归公式定义的。这个著名的递推公式的发现是B样条理论的最重要的进展。

B样条基的性质：

1. 递推性。由递推公式可以表明；
2. 局部支承性。局部支承性表明B样条基是定义在整个参数轴上，但仅在支承区间上有大于零的值，在这个区间外均为零。B样条由其支承区间内的所有节点决定。
3. 规范性。

    

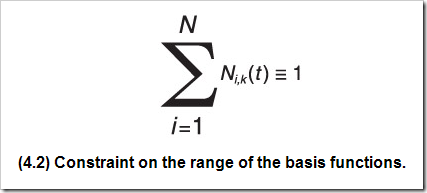
4. 可微性。在节点区间内部是无限次可微的。

这些公式初看起来很吓人，其实不然，只要你理解它们都是做什么用的。画Bezier曲线时，可以根据Bernstein基函数很容易就推出一个基函数。现在必须根据阶数来递推去找到基函数。从一阶基函数开始推导，因为便于图示和举例。

想像一下我想用四个控制顶点画一个四阶三次曲线，我选择节点矢量为[X] = [0, 0, 0, 0, 1, 1, 1, 1]。在继续后面内容之前，用图4.3中的术语来考虑一下这个节点矢量。这个节点矢量让每个控制顶点的改变都会影响到整条曲线，听起来很耳熟？