OpenCascade中网格的数据结构
Mesh Data Structure in OpenCascade
eryar@163.com
摘要Abstract:本文对网格数据结构作简要介绍,并结合使用OpenCascade中的数据结构,将网格数据在OpenSceneGraph中可视化。
关键字KeyWords:OpenCascade、OpenSceneGraph、Triangulation、Mesh Data Structure
一、引言 Introduction
三角网格就是全部由三角形组成的多边形网格。多边形和三角网格在图形学和建模中广泛使用,用来模拟复杂物体的表面,如建筑、车辆、人体,当然,还有茶壶等自由曲面。任意多边形网格都能转换成三角网格。三角网格以其简单性而吸引人,相对于一般多边形网格许多操作对三角网格列容易。
常用的网格数据文件有:
1.Wavefront OBJ(*.obj)
2.3D Max(*.max, *.3ds)
3.VRML(*.vrl)
4.Inventor(*.iv)
5.PLY(*.ply, *.ply2)
6.STL(*.stl)
7.Off(*.off) in CGAL library
有些文件以文本方式保存,有些可以以二进制方式保存。如下图所示为OBJ文件的格式:

Figure 1.1 Wavefront OBJ File Format
l Vertices
n 以‘V’开始;
n 其后为坐标值(x,y,z);
l Faces
n 以‘F’开始;
n 其后为面的顶点索引值;
l Other properties
n Normal, texture coordinates, material, etc.
二、三角网格的表示 Mesh Data Structure
三角网格为一个三角形列表,所以最直接的表示方法是用三角形数组:
struct Triangle
{
Vector3 p[3];
};
struct TriangleMesh
{
int triCount;
Triangle* triList;
};
对于某些应用程序,这种表示方法已经足够。然而,术语“网格”隐含的相邻三角形的连通性未在这种简单表示中有任何体现。实际应用中出现的三角网格,每个三角形都和其他三角形共享边。于是三角网格需要存储三类信息:
l 顶点。每个三角形有三个顶点,各顶点都有可能和其他三角形共享;
l 边。连接两个顶点的边,每个三角形有三条边;
l 面。每个三角形对应一个面。我们可以用顶点或边列表表示面;
根据应用程序的不同,有多种有效的网格表示方法。常用的一种标准的存储格式为索引三角网格。
在索引三角网格中,我们维护了两个列表:顶点表与三角形表。每个顶点包含一个3D位置,也可能有表面法向量、纹理映射坐标、光照值附加数据。每个三角形由顶点列表的三个索引值组成。通常顶点列出的顺序是非常重要的,因为我们必须考虑面的“正面”和“反面”。从前面看时,我们将用顺时针方向列出顶点。
在OpenCascade中,分别用类TColgp_Array1OfPnt和Poly_Array1OfTriangle表存储顶点表和三角形表。注意到索引三角形列表中的邻接信息是隐含的,即边信息没有存储,但我们可以通过搜索三角形表找出公共边。和前面“三角形数组”方式相比,这种方式确实能节省不少空间。原因是信息存于顶点级别,它的整数索引比之三角形数组里存储的顶点重复率要小得多。实践中,三角网里确实有大量的连接性问题。
简单索引三角网格对于基本应用已经足够了。但为更加高效地实现某些操作还可以进一步改进。主要的问题是邻接信息没有显式表达,所以必须从三角形列表中搜索。另一种表达方法可以常数时间内取得这种信息。方法是显式维护一个边列表,每边由两个端点定义,同时维护一个共享该边的三角形列表。这样三角形可视为三条边而非三个点的列表,也就是说它是边列表的索引。该思想的一个扩展称作“Winged Edge”模型(翼边模型),对每一顶点,存储使用该点的边的索引。这样三角形和边都可以通过定位点列表快速查找。
大多数显卡并不直接支持索引三角网。渲染三角形时,一般是将三个顶点同时提交。这样,共享顶点会多次提交,三角形用到一次就提交一次。因为内存和图形硬件间的数据传输是瓶颈,所以许多API和硬件支持特殊三角网格式以减少传输量。基本思想是排序点和面,使得显存中已有的三角形不需要再次传输。
从最高灵活性到最低灵活性,我们讨论三种方案:
n 顶点缓存;
n 三角带Triangle Strip;
n 三角扇Triangle Fan;
三、程序示例 Code Example
在安装好的CGAL库中发现其例子中有很多off文件,其格式同常见的网格文件格式基本相同,结合OpenCascade和OpenSceneGraph,读取off文件,将其表示的网格模型显示出来。程序代码如下所示:
1 /*
2 * Copyright (c) 2013 eryar All Rights Reserved.
3 *
4 * File : Main.cpp
5 * Author : eryar@163.com
6 * Date : 2013-08-10 18:02
7 * Version : V1.0
8 *
9 * Description : Mesh Viewer for the general mesh file format.
10 * Poly_Triangulation data structure can save vertices and triangle index.
11 *
12 */
13
14 // OpenSceneGraph library.
15 #include <osgDB/ReadFile>
16 #include <osgViewer/Viewer>
17 #include <osgGA/StateSetManipulator>
18 #include <osgViewer/ViewerEventHandlers>
19
20 #pragma comment(lib, "osgd.lib")
21 #pragma comment(lib, "osgDBd.lib")
22 #pragma comment(lib, "osgGAd.lib")
23 #pragma comment(lib, "osgViewerd.lib")
24
25 // OpenCascade library.
26 #include <TColgp_Array1OfPnt.hxx>
27 #include <Poly_Array1OfTriangle.hxx>
28 #include <Poly_Triangulation.hxx>
29
30 #pragma comment(lib, "TKernel.lib")
31 #pragma comment(lib, "TKMath.lib")
32
33 /**
34 * @breif Build the mesh from *.off file.
35 */
36 osg::Node* buildMesh(const std::string& fileName)
37 {
38 std::ifstream offFile(fileName.c_str());
39 std::string strBuffer;
40
41 osg::ref_ptr<osg::Geode> geode = new osg::Geode();
42 osg::ref_ptr<osg::Geometry> triGeom = new osg::Geometry();
43 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array();
44 osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array();
45
46 Standard_Integer nbNodes = 0;
47 Standard_Integer nbTriangles = 0;
48
49 // Ignore "OFF"
50 offFile>>strBuffer;
51 offFile>>nbNodes>>nbTriangles>>strBuffer;
52
53 TColgp_Array1OfPnt nodes(0, nbNodes);
54 Poly_Array1OfTriangle triangles(0, nbTriangles);
55
56 // Read node coordinate and store them.
57 Standard_Real dx = 0.0;
58 Standard_Real dy = 0.0;
59 Standard_Real dz = 0.0;
60
61 for (Standard_Integer i = 0; i < nbNodes; i++)
62 {
63 offFile>>dx>>dy>>dz;
64
65 nodes(i).SetCoord(dx, dy, dz);
66 }
67
68 // Read the triangles
69 Standard_Integer ni = 0;
70 Standard_Integer n1 = 0;
71 Standard_Integer n2 = 0;
72 Standard_Integer n3 = 0;
73
74 for (Standard_Integer i = 0; i < nbTriangles; i++)
75 {
76 offFile>>ni>>n1>>n2>>n3;
77
78 triangles(i).Set(n1, n2, n3);
79 }
80
81 // Construct the mesh data by Poly_Triangulation.
82 gp_Pnt node1;
83 gp_Pnt node2;
84 gp_Pnt node3;
85 Poly_Triangle triangle;
86 Handle_Poly_Triangulation T = new Poly_Triangulation(nodes, triangles);
87
88 for (Standard_Integer i = 0; i < nbTriangles; i++)
89 {
90 triangle = triangles.Value(i);
91
92 triangle.Get(n1, n2, n3);
93
94 node1 = nodes.Value(n1);
95 node2 = nodes.Value(n2);
96 node3 = nodes.Value(n3);
97
98 gp_XYZ vector12(node2.XYZ() - node1.XYZ());
99 gp_XYZ vector13(node3.XYZ() - node1.XYZ());
100 gp_XYZ normal = vector12.Crossed(vector13);
101 Standard_Real rModulus = normal.Modulus();
102
103 if (rModulus > gp::Resolution())
104 {
105 normal.Normalize();
106 }
107 else
108 {
109 normal.SetCoord(0., 0., 0.);
110 }
111
112 vertices->push_back(osg::Vec3(node1.X(), node1.Y(), node1.Z()));
113 vertices->push_back(osg::Vec3(node2.X(), node2.Y(), node2.Z()));
114 vertices->push_back(osg::Vec3(node3.X(), node3.Y(), node3.Z()));
115
116 normals->push_back(osg::Vec3(normal.X(), normal.Y(),normal.Z()));
117 }
118
119 triGeom->setVertexArray(vertices.get());
120 triGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::TRIANGLES, 0, vertices->size()));
121 triGeom->setNormalArray(normals);
122 triGeom->setNormalBinding(osg::Geometry::BIND_PER_PRIMITIVE);
123
124 geode->addDrawable(triGeom);
125
126 return geode.release();
127 }
128
129 int main(int argc, char* argv[])
130 {
131 osgViewer::Viewer myViewer;
132
133 std::string strFile;
134
135 (argc > 1) ? strFile = argv[1] : strFile = "ChineseDragon-10kv.off";
136
137 myViewer.setSceneData(buildMesh(strFile));
138
139 myViewer.addEventHandler(new osgGA::StateSetManipulator(myViewer.getCamera()->getOrCreateStateSet()));
140 myViewer.addEventHandler(new osgViewer::StatsHandler);
141 myViewer.addEventHandler(new osgViewer::WindowSizeHandler);
142
143 return myViewer.run();
144 }
程序效果图如下所示:
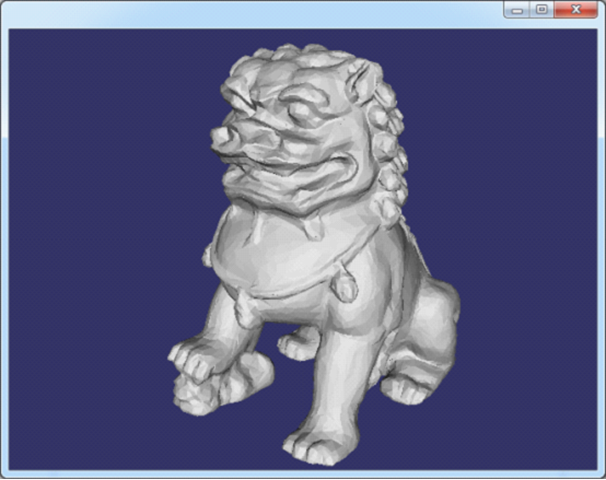
Figure 3.1 ChineseDragon-10kv.off

Figure 3.2 Camel.off

Figure 3.3 cow.off
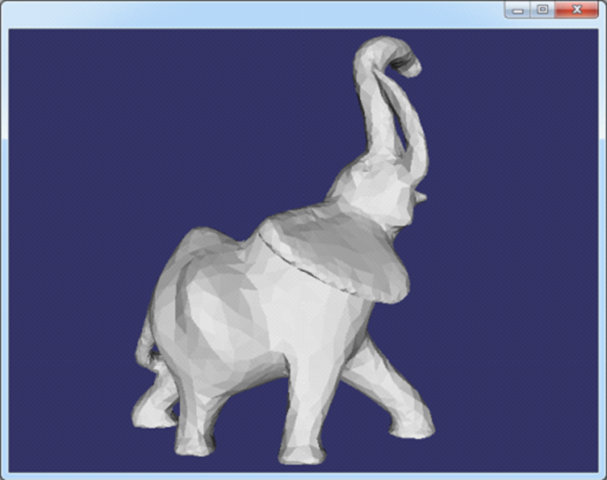
Figure 3.4 elephant.off
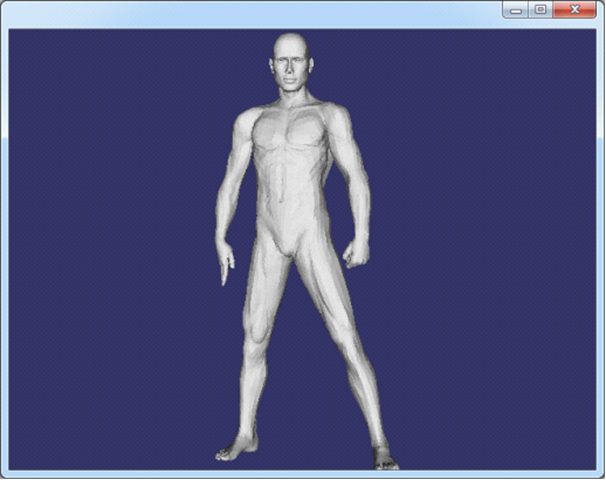
Figure 3.5 man.off
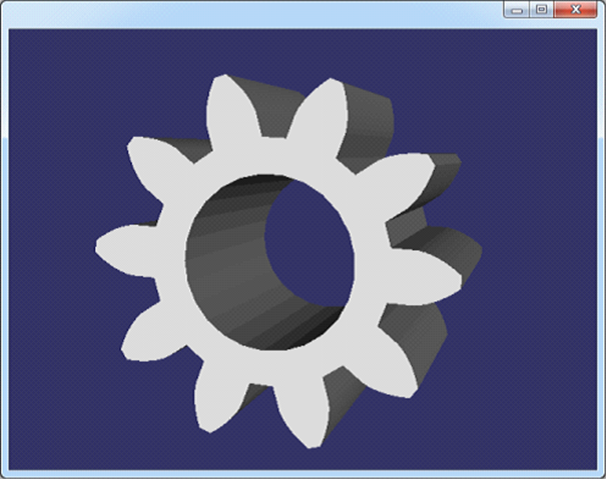
Figure 3.6 pinion.off
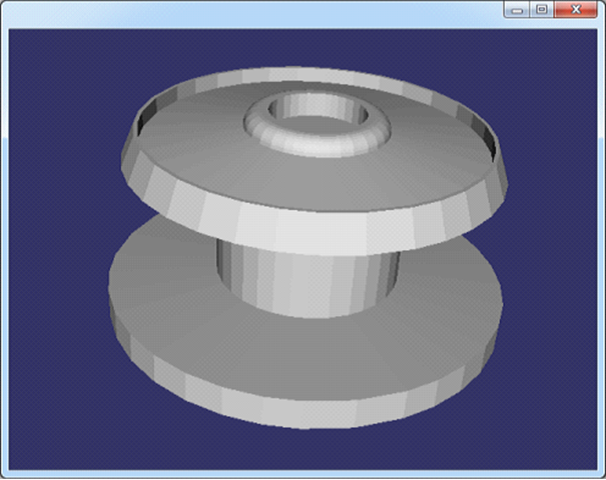
Figure 3.7 spool.off
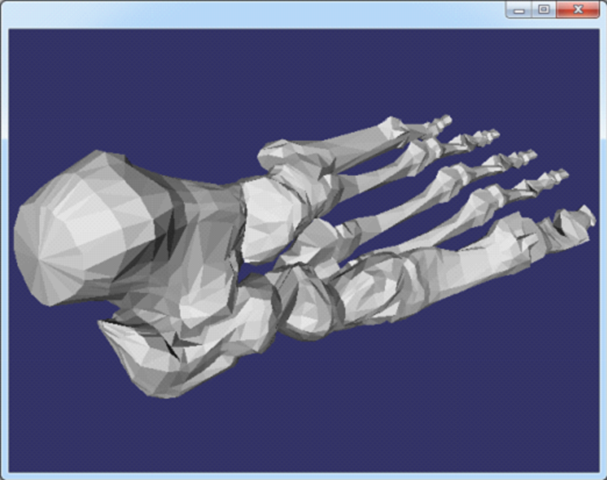
Figure 3.8 bones.off
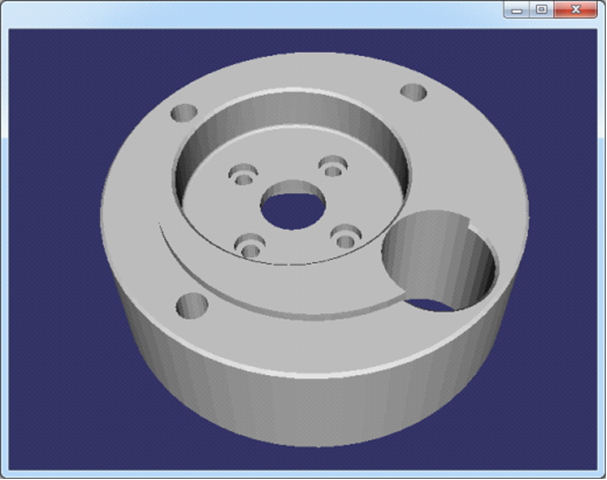
Figure 3.9 couplingdown.off
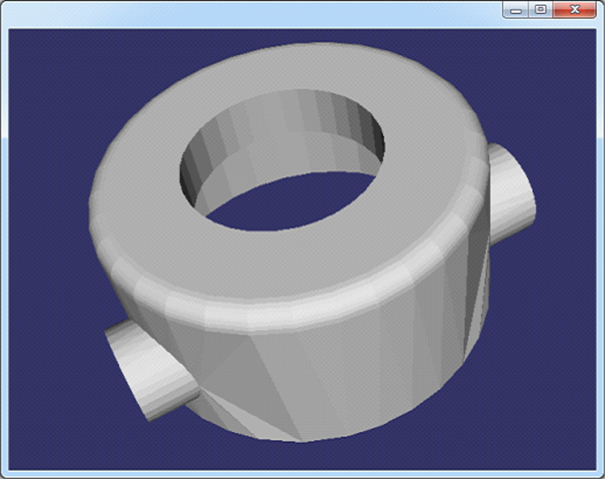
Figure 3.10 rotor.off
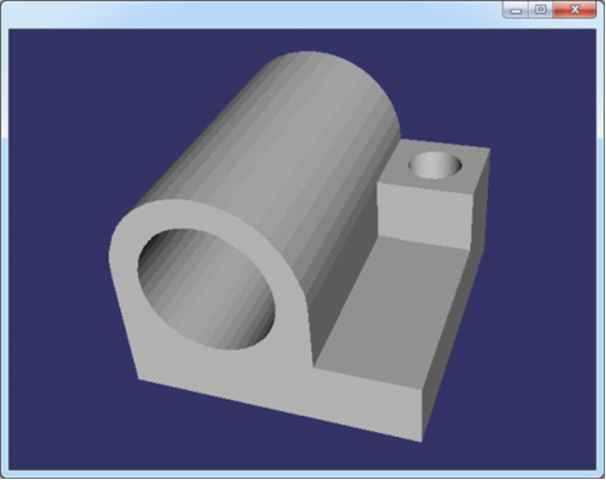
Figure 3.11 joint.off
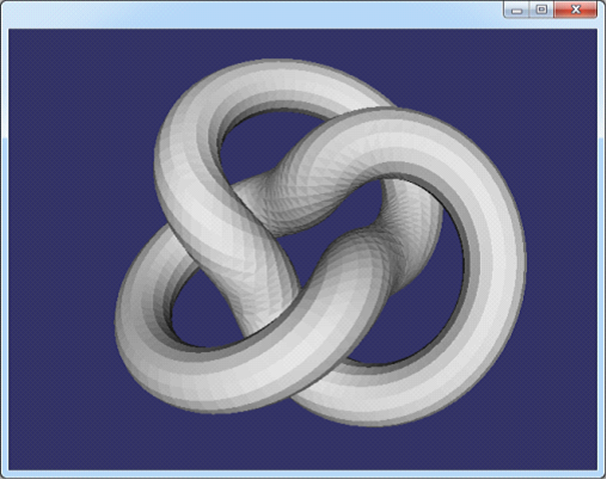
Figure 3.12 knot1.off

Figure 3.13 anchor.off
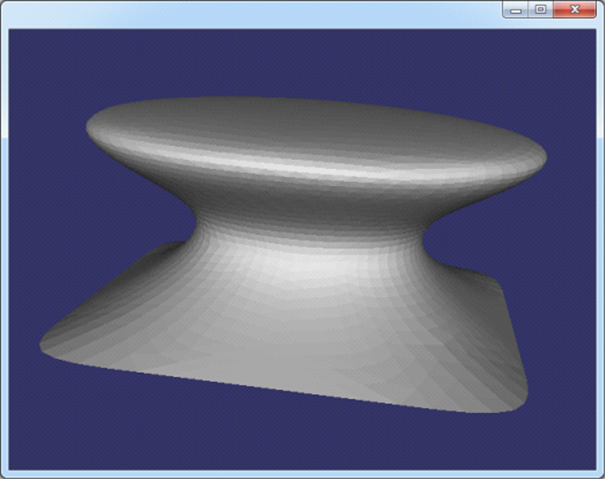
Figure 3.14 mushroom.off
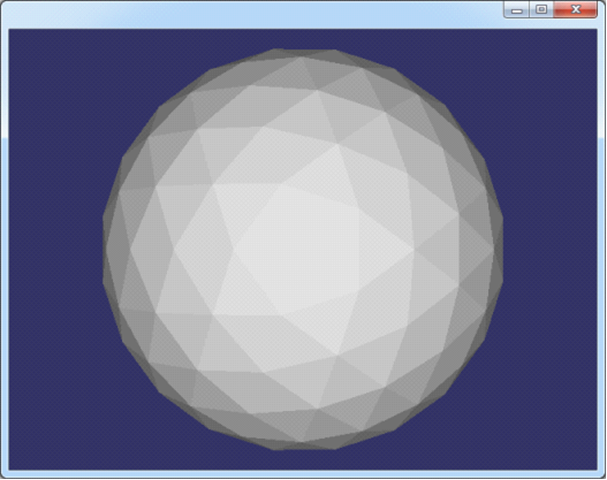
Figure 3.15 sphere.off
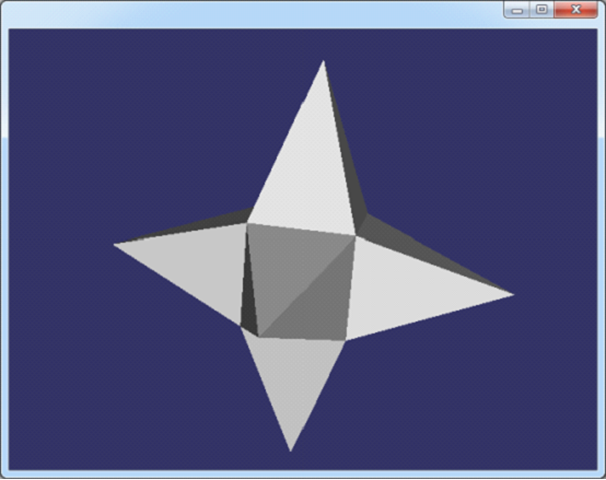
Figure 3.16 star.off
看到这些三维模型,很有感觉!在有关计算机图形学的期刊上有可能也会看到上面的模型。
四、结论 Conclusion
三角网格在计算中用来近似表示三维模型。存储三角网格的标准方式是使用索引三角网格方式。结合OpenCascade中的数据结构,将CGAL示例中的off文件在OpenSceneGraph中显示出来,感觉很棒!