OpenCASCADE 曲线向曲面投影

eryar@163.com

Abstract: Project a curve on a surface no matter the surface is a plane or BSpline Surface. The projected result curve are all BSpline Curve generated by approx algorithm.

Keywords: BRep, Project Curve Surface,

1 Introduction

OpenCASCADE中提供了几何曲线向曲面投影的功能，得到的投影线是曲面上的一条曲线。使用类GeomProjLib的静态函数Project(C, S)和ProjectOnPlane(C, P, D)。

在画法几何与机械制图中，机械图样的绘制是以投影法为依据的。本文主要介绍OpenCASCADE中曲线向曲面投影的实现原理。

2 Project On Plane

在画法几何中投射线互相平行的投影方法叫做平行投影。在平行投影中，以投射线与投影面的关系又可分为正投影法和斜投影法。投射线与投影面相倾斜的平行投影法，叫做斜投影法。投射线与投影面相垂直的平行投影法，叫做正投影法。工程上采用的正投影法来绘制图样。正投影法又因法国学者蒙若(G. Monge, 1746~1818)首次从理论上加以系统阐述而有蒙若法之称。

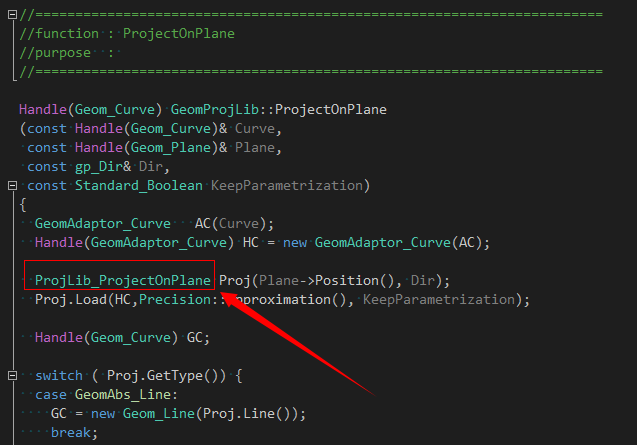
在OpenCASCADE中与平行投影对应的类是ProjLib_ProjectOnPlane，其输入数据有待投影的曲线Curve，投影平面Plane以及投影方向Dir。这里的投影方向Dir与投影平面法向不平行时为斜投影，投影方向Dir与投影平面法向平行时为正投影。

通过查看类ProjLib_ProjectOnPlane的源码实现，可以总结出这个算法的处理流程：

首先输入数据，有待投影的曲线、投影平面及投影方向等。如果投影曲线是特殊曲线，即简单的曲线如直线、圆、椭圆等，计算其投影结果。结果可能还会是简单的曲线。最后处理一般曲线的投影，这时主要使用拟合算法来生成投影曲线，结果都是B样条曲线。

在这个类中我们也可以学习如何使用底层的曲线拟合功能。拟合算法的关键是定义拟合函数。如在此类中，定义的拟合函数ProjLib_OnPlane如下：

主要是实现其中的虚函数Value():

这个函数的作用是计算对应曲线Curve的参数U的空间点在方向D上与平面Pl的交点。可以结合下图写出这个公式：

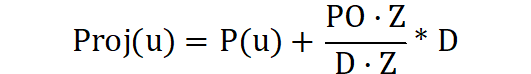
其中P(u)是曲线上对应参数U的点，D是投影方向，Z是平面的法向，O是平面的基点坐标。设P(u)沿投影方向D的长度为x时与平面有交点P1，根据向量P(u)P1与平面法向Z的投影距离与向量P(u)O与平面法向Z的投影距离相等可以列出方程：x*D*Z = PO * Z解出x，即上式中方向D前面的分式。

在看懂这个公式的基础上，建议同学们可以自己写出求1阶微分的公式：

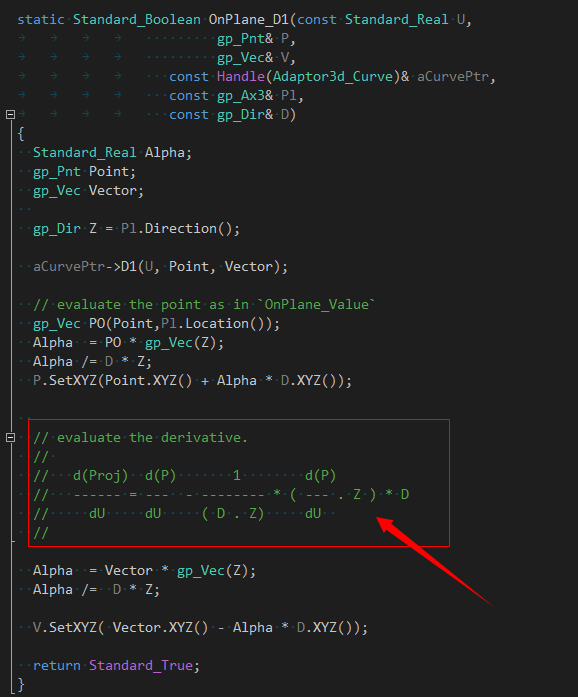
有了拟合函数，就可以调用曲线拟合类来拟合投影曲线：

函数参数中最后一个是拟合曲线的返回值，即一条B样条曲线。

3 Project On Surface

类ProjLib_ProjectOnSurface实现曲线向曲面上的投影，其注释有“Constructs 3D-Curve from the normal projection of the curve on the surface”。其中Normal是曲面法向的意思，还是结合源码来进行说明。

曲线向曲面投影的处理流程与曲线向平面投影类似，关键都是拟合函数的定义。

从实现方法可以看出是通过计算点到曲面的极值来计算对应曲线参数U的点与曲面的交点。这个交点与曲线参数U对应的点的连线方向即曲面在交点处的法向。从而去理解曲面Normal投影的含义，因为在BRep中对应的有相应的投影算法。

4 Conclusion

在OpenCASCADE中曲线向平面投影可以与机械制图中的平行投影对应起来。在处理曲线向曲面投影的算法主要是曲线拟合算法。结合源码理解拟合函数的定义方法，通过对拟合函数的理解，还可以实现曲线向网格面的投影功能。