投影矩阵的实现以及如何从投影矩阵中获取各视裁体平面(教程):
flipcode@msn.com
一.投影的实现:
以D3D为例,先看一下D3D有前设置投影矩阵参数的函数:
D3DXMATRIX *WINAPI D3DXMatrixPerspectiveFovLH(
D3DXMATRIX *pOut,
FLOAT fovy,
FLOAT Aspect,
FLOAT zn,
FLOAT zf
);
第一个是输出的结果,第二个是视角,第三个是屏幕宽高比,第四个是近平面,第五个是远平面.
其实如果不用作视裁剪,只作屏幕投影的话只需用到fovy和aspect,下面我们先求ys的投影,而求出
ys后x的投影xs我们只需根据屏幕宽高比aspect来作一下调整就可以了.
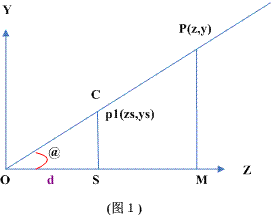
(图1)
o = camera's postion
SC = screen's upper half hight (i.e. screen height/2)
p = a point will project to our screen
d = OS (the distance from O to S)
下面来求ys:
由于OSP1与OMP相似,故
d/z = ys/y
转换一下,得:
ys = d*y/z
现在只差一个未知的d了,
那么d怎么求呢?下面来看一个图:
o = camera's postion
SC = screen's upper half hight (i.e. screen height/2)
d = OA (the distance from O to A)
@ = fov/2
从上图可知tag(@)=SC/d即tag(fov/2)=SC/d,其中fov是已知的(由参数传进),
那么SC呢?查看D3D的文档知道D3D的project空间的
可视范围定义为x∈[-1,1], y∈[-1,1], z∈[0,1]的一个长方体(下面图2和图3)。
(注:ogl的是z∈[[1,1])
从project空间的z负半轴看看我们的变换目标
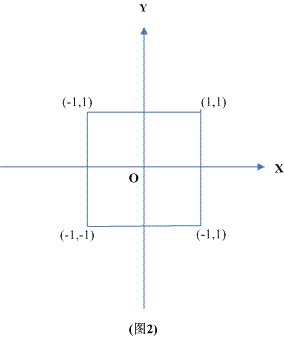
从project空间的x正半轴看看我们的变换目标
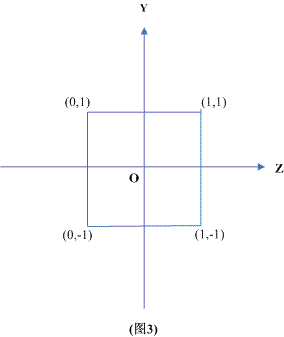
这可看作中间坐标系,从这个坐标系到屏幕坐标只需作放缩和平移操作即可
这样定义的好处是避免一些设备相关性的东西来分散我们的注意力,集中把算法
弄好后而在最后再作调整就可以了.
从上图看出SC=1,故d=1/tag(fov/2)=cot(fov/2);
好,经过这么一番折腾我们最终得到了ys= y*d/z=y*cot(fov/2)/z;
而xs计算同理,但是由于屏幕宽高实际上是不等的,所以可通过参数aspect纵横比
进行调整,xs=x*cot(fov/2)/z/aspect;,另外为了得以使用矩阵乘法,
我们可以利用w分量来保存z(因为w分量在投影矩阵之前都没用到过),
最后才让x/w,y/w来得到正确的投影值,
从而可以得到矩阵如下:
d/aspect 0 0 0
0 d 0 0
0 0 1 1
0 0 0 0
(其中d=cot(fov/2))
二.裁剪:
由上面矩阵我们就可以将一个三维的物体坐标转投影转换到二维的屏幕空间了,但是为了
去掉那些离摄象相很近或是在摄象机后面(投影会变反)或是离摄像很远的物体从而减轻
渲染的负担(以及修正反向投影),我们还要处理一个要投影到(0-1)的z分量.
而这个时候就要用到D3DXMatrixPerspectiveFovLH的最后两个参数了(i.e.近平面及远平面)
下面来讨论它:
如图:
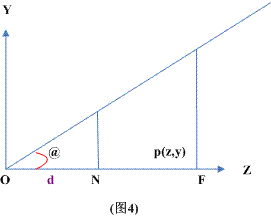
o = camera's postion
@ = fov/2
N = near plane
F = far plane
p = a point will project to our screen
从上图可以看到N就是我们要作裁剪用的近平面,而F就是我们要作裁剪用远平面,
近平面和远平面可从参数得来,这时我们想作的是让落在N和F上的点映射到0到1的
线性坐标上,也就是说当p的z=N时投影后的zs=0,而当z=F时投影后的zs=1;
这个很好办:zs=(z-N)/(F-N)即可.
好了,这一步也轻松办到了,但是我们前面为了实际用矩阵变换来作投影而让其在
投影后再/w(w保存z值)才是最后的结果. 既然这样那么我们所求的就是还未除过w的
投影值为zw. 想一下,当z=F时我们投影后的zs=zw/z=1,也就是zs=zw/F=1;所以zw=zs*F,
因为前面求得zs=(z-N)/(F-N),所以zw=F*(z-N)/(F-N);(简单验证一下:当z=N时,zw=0,这时
zs=0/w还是0,而当z增大时0<zw<=F,也就是0<zs<=1,而直到z=F时,zw=F,这时zs=F/w=F/F=1),
为了方便将其分解成:zw=(z*F-N*F)/(F-N)=z*F/(F-N)-N*F/(F-N)
这样就可以把它应用到矩阵中,如下:
d/aspect 0 0 0
0 d 0 0
0 0 F/(F-N) 1
0 0 -N*F/(F-N) 0
以上公式可以代替D3DXMatrixPerspectiveFovLH来作测试:
void myMatrixPerspectiveFovLH(mat4 *out, float fov, float aspect, float n, float f)
{
float h = tanf(0.5*fov);
float w = h * aspect;
out = mat4( 1.0f/w, 0, 0, 0
0 1.0f/h 0 0
0 0 f/(f-n) 1
0 0 -n*f/(f-n) 0);
}
其中1.0f/h 就是cot(fov/2), aspect=width/height
三.从投影矩阵获取视裁体:
上面已说过对一点投影后的各分量值所在范围为:
-1<xs<1;
-1<ys<1;
0<zs<1;
其中xs/ys/zs是除过w后的值,而未除过w的值所在范围是:
-w<xw<w; -w<yw<w;
0<zw<w;
对各不等式进分解后得:
xw+w>0;且xw-w<0;
yw+w>0;且yw-w<0;
zw>0;且xw-w<0;
我们知道xw/yw/zw是一个在view space中的点v(xv,yv,zv,wv)(其中wv=1)乘上投影矩阵后的各分量值(当然还未除以w),那么
点v(xv,yv,zv,wv)是如何乘上投影矩阵的呢?是这样的:
xw = xv*prj_11+yv*prj_21*prj_31+wv*prj_41;
zw = xv*prj_12+yv*prj_22*prj_32+wv*prj_42;
zw = xv*prj_13+yv*prj_23*prj_33+wv*prj_43;
w = xv*prj_14+yv*prj_24*prj_34+wv*prj_44;
即:
xw = v dop col1;
yw = v dop col2;
zw = v dop col3;
w = v dop col4;
(说明:上述col1和col2及col3其实表达了一个投影坐标系,其中col1表示x轴,col2表示y轴,col3表示z轴,
而点v乘上这个坐标系就相当于求出点v在此新坐标系中各分量上的投影值,此外col4只是简单的为了让点v点乘它时求得w=原点v的w分量值)
故:
xw+w>0;
即:
v dop col1 + v dop col4 > 0;
即:
v dop ( col1 + col4 ) > 0;
也就是:
xv*(prj_11+prj_14) + yv*(prj_21+prj_24) + zv*(prj_31+prj_34) + wv*(prj_41+prj_44) > 0;
我们知道平面公式是: ax+by+cz+d=0,故上面其实表示的就是视裁体的左平面向内,其中它的法线是:
(prj_11+prj_14), (prj_21+prj_24), (prj_31+prj_34).
而由于wv=1,
故它的距离是(prj_41+prj_44).
同理我们可以求出视裁体的其它平面.
四.Frustum Culling
我们知道,视裁体的六个面是朝向内的,由上面已经得到了各平面等式,只要用P DOP N + D看是否大于0就可以知道点P是否在一个平面
内,最后点P如果在所有平面内的才是在视裁体内.
而当判断一个物体是否在视裁体内时,我们只需对物体的包围盒进行测试,例如,测试一个包围球是否在视裁体内,只要判断所有P DOP N + D
>2的1/2次方*R不等式成立即可.
参考文档:
fast extraction of viewing frustum planes from the world-view-projection matrix