这本书对于入门级的人来说是一个不错的选择,它囊括了很多关于计算机方面的知识,能够使你对这方面的知识有个广泛的了解。
对于小数的存储常用的是浮点记数法。
浮点记数法简介
对于知识的掌握,通过例子的学习是一个很好的方式。为了考虑到例子的简易型,用一个字节来存储浮点数。那么如01101011这样的二进制序列表示的是什么小数呢?
一个字节中浮点记数法有如下成分:
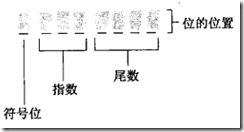
在01101011这么一个串中,符号位是0表示非负,1则表示负,指数为110,表示位数将乘以2^(指数),也就是将小数点从尾数位的最左边移动指数个位,如果指数为正,向右移动;反之,向左移动指数位。110是用余码的方式进行记录的。对于余码,我采用的解析的方式是,将最高为取反,按照补码的方式进行读取。
110--->010,表示2;0100--->1100,表示-4;
既然提到了补码,就解释一下补码,最高位为零的补码其值直接读取,0110--->6;最高为为1的补码,其值的读取方式,从右往左遇到第一个1之后的所有位取反,读出值后加个负号,1101--->0011,则-3。当然对于0和最小的负数,不适合上述的方式,但是也很容易就能给出其值。
再让我们回到0,110,1011这个串中,尾数.1011最左断含有一个小数点,由于110--->2,因此小数点向右移动两位则10.11,此时读取值2+1/2+1/4=2又3/4。
至此,我们已经知道小数是如何存储在二进制串中,也知道了如何将其转换为10进制数值,那么该提出注意事项的时候了。
1. 规范化形式
尾数最左端的一位必须是1,否则会出现多意的现象。如00111100,01000110,都可以解码为3/8。
2. 截断误差
整型值会出现溢出现象,同样浮点数也会出现类似的现象。如利用一字节浮点记数法存储值2又5/8,先用二进制进行表示10.101,而尾数只有4位,因此会出现截断。
还有一个需要注意的是浮点记数法表示的数值加法中,它们相加的顺序很重要。
如,2+1/4+1/8+1/8+1/8+1/8,当到2(5/8)+1/8时,2(5/8)用二进制表示为10.101,这将发生截断,变成10.10,继续加1/8则会持续阶段。当反过来进行加法运算时,则不会出现截断的现象。
由于实际浮点数具有较长的位数,能够较好的运用于一般的浮点数运算中。但是这样的问题在一些应用中是很严重的(如航海系统),小的误差在不断的加法运算中累加,最终产生严重的后果,因此对于精度要求较好的运算中,可以选择采用分数表示法,分装一个表示分数的类。