一、数论算法
1．求两数的最大公约数
2．求两数的最小公倍数
3．素数的求法
A.小范围内判断一个数是否为质数：
B.判断longint范围内的数是否为素数（包含求50000以内的素数表）：

二、图论算法
1．最小生成树
A.Prim算法：
B.Kruskal算法：(贪心)
按权值递增顺序删去图中的边，若不形成回路则将此边加入最小生成树。
2.最短路径
A.标号法求解单源点最短路径：
B.Floyed算法求解所有顶点对之间的最短路径：
C. Dijkstra 算法：
3.计算图的传递闭包
4．无向图的连通分量
A.深度优先
B 宽度优先（种子染色法）
5．关键路径
几个定义： 顶点1为源点，n为汇点。
a. 顶点事件最早发生时间Ve[j], Ve [j] = max{ Ve [j] + w[I,j] },其中Ve (1) = 0;
b. 顶点事件最晚发生时间 Vl[j], Vl [j] = min{ Vl[j] – w[I,j] },其中 Vl(n) = Ve(n);
c. 边活动最早开始时间 Ee[I], 若边I由<j,k>表示，则Ee[I] = Ve[j];
d. 边活动最晚开始时间 El[I], 若边I由<j,k>表示，则El[I] = Vl[k] – w[j,k];
若 Ee[j] = El[j] ，则活动j为关键活动，由关键活动组成的路径为关键路径。
求解方法：
a. 从源点起topsort,判断是否有回路并计算Ve;
b. 从汇点起topsort,求Vl;
c. 算Ee 和 El;
6．拓扑排序
找入度为0的点，删去与其相连的所有边，不断重复这一过程。
例 寻找一数列，其中任意连续p项之和为正，任意q 项之和为负，若不存在则输出NO.
7.回路问题
Euler回路(DFS)
定义：经过图的每条边仅一次的回路。（充要条件：图连同且无奇点）
Hamilton回路
定义：经过图的每个顶点仅一次的回路。
一笔画
充要条件：图连通且奇点个数为0个或2个。
9．判断图中是否有负权回路 Bellman-ford 算法
x[I],y[I],t[I]分别表示第I条边的起点，终点和权。共n个结点和m条边。
10．第n最短路径问题
*第二最短路径：每举最短路径上的每条边，每次删除一条，然后求新图的最短路径，取这些路径中最短的一条即为第二最短路径。
*同理，第n最短路径可在求解第n-1最短路径的基础上求解。

三、背包问题
*部分背包问题可有贪心法求解：计算Pi/Wi
数据结构：
w[i]:第i个背包的重量；
p[i]:第i个背包的价值；
1．0-1背包： 每个背包只能使用一次或有限次(可转化为一次)：
A.求最多可放入的重量。
B.求可以放入的最大价值。
F[I,j] 为容量为I时取前j个背包所能获得的最大价值。
F [i,j] = max { f [ i – w [ j ], j-1] + p [ j ], f[ i,j-1] }
C.求恰好装满的情况数。
2．可重复背包
A求最多可放入的重量。
F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志，为布尔型。
状态转移方程为
f[I,j] = f [ I-1, j – w[I]*k ] (k=1.. j div w[I])
B.求可以放入的最大价值。
f[i,j] = max { f [i- k*w[j], j-1] + k*p[j] } (0<=k<= i div w[j])
其中f[i,j]表示容量为i时取前j种背包所能达到的最大值。
C.求恰好装满的情况数。
Ahoi2001 Problem2
求自然数n本质不同的质数和的表达式的数目。
思路一，生成每个质数的系数的排列，在一一测试，这是通法。
思路二，递归搜索效率较高

思路三：可使用动态规划求解
四、排序算法
1.快速排序：
B.插入排序：
思路：当前a[1]..a[i-1]已排好序了，现要插入a[i]使a[1]..a[i]有序。
C.选择排序：
D. 冒泡排序
E.堆排序：
F. 归并排序
G.基数排序
思想：对每个元素按从低位到高位对每一位进行一次排序
五、高精度计算
高精度数的定义：
1．高精度加法
2．高精度减法
3．高精度乘以低精度
4．高精度乘以高精度
5．高精度除以低精度
6．高精度除以高精度

六、 树的遍历
1．已知前序中序求后序
2．已知中序后序求前序
3．已知前序后序求中序的一种

七 进制转换
1任意正整数进制间的互化
除n取余
2实数任意正整数进制间的互化
乘n取整
3负数进制：
设计一个程序，读入一个十进制数的基数和一个负进制数的基数，并将此十进制数转换为此负 进制下的数：-R∈{-2，-3，-4,....-20}
八 全排列与组合的生成
1排列的生成：（1..n）
2组合的生成(1..n中选取k个数的所有方案)

九.查找算法
1折半查找
2树形查找
二叉排序树：每个结点的值都大于其左子树任一结点的值而小于其右子树任一结点的值。
查找

十、贪心
*会议问题
（1） n个活动每个活动有一个开始时间和一个结束时间，任一时刻仅一项活动进行，求满足活动数最多的情况。
解：按每项活动的结束时间进行排序，排在前面的优先满足。
（2）会议室空闲时间最少。
（3）每个客户有一个愿付的租金，求最大利润。
（4）共R间会议室，第i个客户需使用i间会议室，费用相同，求最大利润。
十一、回溯法框架
1. n皇后问题
2.Hanoi Tower h(n)=2*h(n-1)+1 h(1)=1

十二、DFS框架

十三、BFS框架

十五、数据结构相关算法
1．链表的定位函数

2．单链表的插入操作
3．单链表的删除操作
4．双链表的插入操作（插入新结点q）
5．双链表的删除操作

原文链接：http://old.blog.edu.cn/user3/Hailer/archives/2006/1545396.shtml

     摘要: FOJ Hotter Colder http://acm.fzu.edu.cn/problem.php?pid=1014 求线段的中位线，线段相交求交点，求凸多边形的面积， 无归之室 http://acm.fzu.edu.cn/problem.php?pid=1016 本题精度要求非常高，用三角函数的话，很容易就wa.. Reflections http://acm.fzu.e...  阅读全文

Euler的任意四面体体积公式（已知边长求体积）

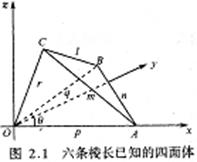
已知4点坐标求体积（其中四个点的坐标分别为（x1,y1,z1）,（x2,y2,z2）,（x3,y3,z3）,（x4,y4,z4）

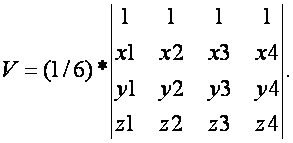
注意事项：

1. 注意舍入方式(0.5的舍入方向);防止输出-0.

2. 几何题注意多测试不对称数据.

3. 整数几何注意xmult和dmult是否会出界;

   符点几何注意eps的使用.

4. 避免使用斜率;注意除数是否会为0.

5. 公式一定要化简后再代入.

6. 判断同一个2*PI域内两角度差应该是

   abs(a1-a2)<beta||abs(a1-a2)>pi+pi-beta;

   相等应该是

   abs(a1-a2)<eps||abs(a1-a2)>pi+pi-eps;

7. 需要的话尽量使用atan2,注意:atan2(0,0)=0,

   atan2(1,0)=pi/2,atan2(-1,0)=-pi/2,atan2(0,1)=0,atan2(0,-1)=pi.

8. cross product = |u|*|v|*sin(a)

   dot product = |u|*|v|*cos(a)

9. (P1-P0)x(P2-P0)结果的意义:

   正: <P0,P1>在<P0,P2>顺时针(0,pi)内

   负: <P0,P1>在<P0,P2>逆时针(0,pi)内

   0 : <P0,P1>,<P0,P2>共线,夹角为0或pi

原文链接：http://cschf.spaces.live.com/blog/cns!E113B8D05D833E2B!140.entry
写几点不熟悉的
12. 判断点是否在多边形中
13. 判断线段是否在多边形内
25. 计算线段或直线与线段的交点
27. 求线段或直线与圆的交点

判断点是否在多边形中：

判断点P是否在多边形中是计算几何中一个非常基本但是十分重要的算法。以点P为端点，向左方作射线L，由于多边形是有界的，所以射线L的左端一定在多边形外，考虑沿着L从无穷远处开始自左向右移动，遇到和多边形的第一个交点的时候，进入到了多边形的内部，遇到第二个交点的时候，离开了多边形，……所以很容易看出当L和多边形的交点数目C是奇数的时候，P在多边形内，是偶数的话P在多边形外。

但是有些特殊情况要加以考虑。如图下图(a)(b)(c)(d)所示。在图(a)中，L和多边形的顶点相交，这时候交点只能计算一个；在图(b)中，L和多边形顶点的交点不应被计算；在图(c)和(d) 中，L和多边形的一条边重合，这条边应该被忽略不计。如果L和多边形的一条边重合，这条边应该被忽略不计。

为了统一起见，我们在计算射线L和多边形的交点的时候，1。对于多边形的水平边不作考虑；2。对于多边形的顶点和L相交的情况，如果该顶点是其所属的边上纵坐标较大的顶点，则计数，否则忽略；3。对于P在多边形边上的情形，直接可判断P属于多边行。由此得出算法的伪代码如下：
    count ← 0;
    以P为端点，作从右向左的射线L; 
    for 多边形的每条边s
     do if P在边s上 
          then return true;
        if s不是水平的
          then if s的一个端点在L上
                 if 该端点是s两端点中纵坐标较大的端点
                   then count ← count+1
               else if s和L相交
                 then count ← count+1;
    if count mod 2 = 1 
      then return true;
    else return false;
其中做射线L的方法是：设P'的纵坐标和P相同，横坐标为正无穷大（很大的一个正数），则P和P'就确定了射线L。

判断点是否在多边形中的这个算法的时间复杂度为O(n)。

另外还有一种算法是用带符号的三角形面积之和与多边形面积进行比较，这种算法由于使用浮点数运算所以会带来一定误差，不推荐大家使用。

判断线段是否在多边形内：

线段在多边形内的一个必要条件是线段的两个端点都在多边形内，但由于多边形可能为凹，所以这不能成为判断的充分条件。如果线段和多边形的某条边内交（两线段内交是指两线段相交且交点不在两线段的端点），因为多边形的边的左右两侧分属多边形内外不同部分，所以线段一定会有一部分在多边形外(见图a)。于是我们得到线段在多边形内的第二个必要条件：线段和多边形的所有边都不内交。

线段和多边形交于线段的两端点并不会影响线段是否在多边形内；但是如果多边形的某个顶点和线段相交，还必须判断两相邻交点之间的线段是否包含于多边形内部（反例见图b)。

 

因此我们可以先求出所有和线段相交的多边形的顶点，然后按照X-Y坐标排序(X坐标小的排在前面，对于X坐标相同的点，Y坐标小的排在前面，这种排序准则也是为了保证水平和垂直情况的判断正确)，这样相邻的两个点就是在线段上相邻的两交点，如果任意相邻两点的中点也在多边形内，则该线段一定在多边形内。

证明如下：

命题1：
如果线段和多边形的两相邻交点P1 ，P2的中点P' 也在多边形内，则P1, P2之间的所有点都在多边形内。

证明：
假设P1,P2之间含有不在多边形内的点，不妨设该点为Q，在P1, P'之间，因为多边形是闭合曲线，所以其内外部之间有界，而P1属于多边行内部，Q属于多边性外部，P'属于多边性内部，P1-Q-P'完全连续，所以P1Q和QP'一定跨越多边形的边界，因此在P1,P'之间至少还有两个该线段和多边形的交点，这和P1P2是相邻两交点矛盾，故命题成立。证毕。

由命题1直接可得出推论：
推论2：
设多边形和线段PQ的交点依次为P1,P2,……Pn，其中Pi和Pi+1是相邻两交点，线段PQ在多边形内的充要条件是：P，Q在多边形内且对于i =1, 2,……, n-1，Pi ,Pi+1的中点也在多边形内。
在实际编程中，没有必要计算所有的交点，首先应判断线段和多边形的边是否内交，倘若线段和多边形的某条边内交则线段一定在多边形外；如果线段和多边形的每一条边都不内交，则线段和多边形的交点一定是线段的端点或者多边形的顶点，只要判断点是否在线段上就可以了。
至此我们得出算法如下：
    if 线端PQ的端点不都在多边形内 
      then return false;
    点集pointSet初始化为空;
    for 多边形的每条边s
      do if 线段的某个端点在s上
           then 将该端点加入pointSet;
         else if s的某个端点在线段PQ上
           then 将该端点加入pointSet;
         else if s和线段PQ相交 // 这时候已经可以肯定是内交了
           then return false;
    将pointSet中的点按照X-Y坐标排序;
    for pointSet中每两个相邻点 pointSet[i] , pointSet[ i+1]
      do if pointSet[i] , pointSet[ i+1] 的中点不在多边形中
           then return false;
    return true;
这个过程中的排序因为交点数目肯定远小于多边形的顶点数目n，所以最多是常数级的复杂度，几乎可以忽略不计。因此算法的时间复杂度也是O(n)。

计算线段或直线与线段的交点:

设一条线段为L0 = P1P2，另一条线段或直线为L1 = Q1Q2 ，要计算的就是L0和L1的交点。
1． 首先判断L0和L1是否相交（方法已在前文讨论过），如果不相交则没有交点，否则说明L0和L1一定有交点，下面就将L0和L1都看作直线来考虑。

2． 如果P1和P2横坐标相同，即L0平行于Y轴

a) 若L1也平行于Y轴，

i. 若P1的纵坐标和Q1的纵坐标相同，说明L0和L1共线，假如L1是直线的话他们有无穷的交点，假如L1是线段的话可用"计算两条共线线段的交点"的算法求他们的交点（该方法在前文已讨论过）；
ii. 否则说明L0和L1平行，他们没有交点；

b) 若L1不平行于Y轴，则交点横坐标为P1的横坐标，代入到L1的直线方程中可以计算出交点纵坐标；

3． 如果P1和P2横坐标不同，但是Q1和Q2横坐标相同，即L1平行于Y轴，则交点横坐标为Q1的横坐标，代入到L0的直线方程中可以计算出交点纵坐标；

4． 如果P1和P2纵坐标相同，即L0平行于X轴

a) 若L1也平行于X轴，

i. 若P1的横坐标和Q1的横坐标相同，说明L0和L1共线，假如L1是直线的话他们有无穷的交点，假如L1是线段的话可用"计算两条共线线段的交点"的算法求他们的交点（该方法在前文已讨论过）；
ii. 否则说明L0和L1平行，他们没有交点；

b) 若L1不平行于X轴，则交点纵坐标为P1的纵坐标，代入到L1的直线方程中可以计算出交点横坐标；

5． 如果P1和P2纵坐标不同，但是Q1和Q2纵坐标相同，即L1平行于X轴，则交点纵坐标为Q1的纵坐标，代入到L0的直线方程中可以计算出交点横坐标；

6． 剩下的情况就是L1和L0的斜率均存在且不为0的情况

a) 计算出L0的斜率K0，L1的斜率K1 ；

b) 如果K1 = K2 

i. 如果Q1在L0上，则说明L0和L1共线，假如L1是直线的话有无穷交点，假如L1是线段的话可用"计算两条共线线段的交点"的算法求他们的交点（该方法在前文已讨论过）；
ii. 如果Q1不在L0上，则说明L0和L1平行，他们没有交点。
c) 联立两直线的方程组可以解出交点来
这个算法并不复杂，但是要分情况讨论清楚，尤其是当两条线段共线的情况需要单独考虑，所以在前文将求两条共线线段的算法单独写出来。另外，一开始就先利用矢量叉乘判断线段与线段（或直线）是否相交，如果结果是相交，那么在后面就可以将线段全部看作直线来考虑。需要注意的是，我们可以将直线或线段方程改写为ax+by+c=0的形式，这样一来上述过程的部分步骤可以合并，缩短了代码长度，但是由于先要求出参数，这种算法将花费更多的时间。

求线段或直线与圆的交点:

设圆心为O，圆半径为r，直线（或线段）L上的两点为P1,P2。

1. 如果L是线段且P1，P2都包含在圆O内，则没有交点；否则进行下一步。

2. 如果L平行于Y轴，

a) 计算圆心到L的距离dis；
b) 如果dis > r 则L和圆没有交点；
c) 利用勾股定理，可以求出两交点坐标，但要注意考虑L和圆的相切情况。
3. 如果L平行于X轴，做法与L平行于Y轴的情况类似；

4. 如果L既不平行X轴也不平行Y轴，可以求出L的斜率K，然后列出L的点斜式方程，和圆方程联立即可求解出L和圆的两个交点；

5. 如果L是线段，对于2，3，4中求出的交点还要分别判断是否属于该线段的范围内。

一、点的基本运算
1. 平面上两点之间距离 1
2. 判断两点是否重合 1
3. 矢量叉乘 1
4. 矢量点乘 2
5. 判断点是否在线段上 2
6. 求一点饶某点旋转后的坐标 2
7. 求矢量夹角 2

二、 线段及直线的基本运算
1. 点与线段的关系 3
2. 求点到线段所在直线垂线的垂足 4
3. 点到线段的最近点 4
4. 点到线段所在直线的距离 4
5. 点到折线集的最近距离 4
6. 判断圆是否在多边形内 5
7. 求矢量夹角余弦 5
8. 求线段之间的夹角 5
9. 判断线段是否相交 6
10.判断线段是否相交但不交在端点处（内交） 6
11.求线段所在直线的方程 6
12.求直线的斜率 7
13.求直线的倾斜角 7
14.求点关于某直线的对称点 7
15.判断两条直线是否相交及求直线交点 7
16.判断线段是否相交，如果相交返回交点 7

三、多边形常用算法模块
1. 判断多边形是否简单多边形 8
2. 检查多边形顶点的凸凹性 9
3. 判断多边形是否凸多边形 9
4. 求多边形面积 9
5. 判断多边形顶点的排列方向，方法一 10
6. 判断多边形顶点的排列方向，方法二 10
7. 射线法判断点是否在多边形内 10
8. 判断点是否在凸多边形内 11
9. 寻找点集的graham算法 12
10.寻找点集凸包的卷包裹法 13
11.判断线段是否在多边形内 14
12.求简单多边形的重心 （HDU1115）15
13.求凸多边形的重心 17
14.求肯定在给定多边形内的一个点 17
15.求从多边形外一点出发到该多边形的切线 18
16.判断多边形的核是否存在 19 

四、 圆的基本运算
1 .点是否在圆内 20
2 .求不共线的三点所确定的圆 21

五、矩形的基本运算
1.已知矩形三点坐标，求第4点坐标 22

六、常用算法的描述 22

七、补充
1．两圆关系： 24
2．判断圆是否在矩形内： 24
3．点到平面的距离： 25
4．点是否在直线同侧： 25
5．镜面反射线： 25
6．矩形包含： 26
7．两圆交点： 27
8．两圆公共面积： 28
9. 圆和直线关系： 29
10. 内切圆： 30
11. 求切点： 31
12. 线段的左右旋： 31
13．公式： 32

附上一篇博客：计算几何算法概览 

 

zoj上的计算几何题
Vol I
1010 by pandahyx
1032 by javaman
1037 by Vegetable Bird
1041 by javaman
1081 by Vegetable Bird
1090 by Vegetable Bird

Vol II
1104 by javaman
1123 by javaman
1139 by Vegetable Bird
1165 by javaman
1199 by Vegetable Bird

Vol V
1426 by Vegetable Bird
1439 by Vegetable Bird
1460 by Vegetable Bird
1472 by Vegetable Bird

Vol VI
1597 by Vegetable Bird

Vol VII
1608 by Vegetable Bird
1648 by Vegetable Bird

Vol XII
2102 by pandahyx
2107 by pandahyx
2157 by pandahyx

Vol XIII
2234 by pandahyx

Vol XIV
2318 by ahyangyi
2394 by qherlyt

Vol XV
2403 by Vegetable Bird

 1.  一种是用矢量叉乘法：
        由三个顶点向所求的点引出矢量（注意方向），然后任意用其中两个矢量形成平面，再用这个平面和剩下的矢量叉乘，得出一个新矢量，方向向里，则在三角形外，反之在里面。
2.用面积方法

题目：一共来了n(0<n<25)个同学，按照组队规则（自由组队，每队人数不限），一共会有多少种不同的组队方案呢？
递推式是：a[i][j]=a[i-1][j-1]+a[i-1][j]*j;

而且。a[i][0]应该是为0，不为1的。

此外还得注溢出。要用__int64类型。
http://acm.hdu.edu.cn/showproblem.php?pid=1292

在ICPC比赛中，个人能力方面，如果粗略地分的话，大致可以分为算法能力、代码能力和查错能力。那些大学才开始参加比赛的选手，写代码的基本功一般会比较扎实，主要瓶颈应该是算法能力。而对于OI转ICPC的选手来说，代码能力往往是最大的缺陷。随着OI转ICPC的选手逐渐增多，代码能力的问题愈发暴露了出来。

一、如何定义代码能力

Comars曾经给代码能力作过一个比较准确的定义。2004年暑假时，Comars曾经说过：他认为150行以内的题目，他的1Y率非常高，并且保持稳定；而当代码长度超过150行以后，1Y率就开始急速下降了。如果我们画出一条1Y率的曲线的话，150行就是一个转折点。我们不妨认为，150行就是Comars当时的代码能力。一年以后，经过努力，Comars把代码能力提高到了250行。不过，这已经是后话了。

二、如何提高代码能力

我一直觉得写程序和写文章是一个对很好的类比。

写文章需要先从宏观入手，构思文章的结构。写程序同样需要。一个好的结构，就是一个好的开始。一个好的开始，是成功的一半。
一篇好的文章需要各种句式和词藻的合理组合。体现到写程序上来，就是一些单句以及三五行的小结构的熟练使用。这些都是需要平时总结和积累的。

但凡文章写得好的人，一定看过很多别人写的文章。同样的道理，多看别人的程序，用心地去看，也可以提高自己的代码能力。
我鼓励队员去看别人写的程序，特别是像Comars这样的选手写的程序。从优秀的程序中，我们可以体会别人良好的程序结构，同时也可以学到很多写程序的技巧――三五行的小技巧。在和Comars做队友的两年时间里，我通过看Comars的程序，学会了很多小技巧。逐渐地，我觉得我写的某些程序已经和Comars有点相像了。
那么，如果身边没有Comars这样优秀的选手可以借鉴，该怎么办呢？其实没关系。任何一个程序都是可以看的。一个程序，就算写得再差，总还会有一两个闪光点，要想办法把它们找出来。另外，程序里写得不好的地方，也要一一找出来。
读程序，从某种角度来看，就像读史。好的历史是用来借鉴的；不好的历史则应该引以为戒。读程序也是一样，择其善者而从之，其不善者而改之。

三、谨慎地对待STL和SCL

STL - Standard Template Library。在ICPC的选手中，STL是相当受欢迎的。的确，如果STL用得好，程序可以精简很多。既提高了编程的速度，也提高了编程的准确性。
SCL - Standard Code Library，就是标准程序库。对很多选手来说，SCL可是命根子啊

我觉得STL和SCL都不是坏东西，但是需要谨慎地使用。

我向来不主张队员一进队就开始用STL（虽然这种现象普遍存在 ）。我认为，STL的作用是锦上添花，而不是雪中送炭。比方说，一个heap写得很熟练的队员，我觉得他可以偷偷懒，用一下STL。但是，那些不太会写heap的队员，就不应该用STL里的heap。因为，他们真正应该做的是掌握写heap的能力――这才是最本质的代码能力。
学会用STL是件很爽的事情。但是须知有所得必有所失。如果过早地接触STL，会让你失去很多锻炼代码能力的机会。

至于SCL，我的主张是尽量不用。
不可否认，队里确实有一些人SCL用得很好。但是，我至今仍然没有见过一个SCL用得很好，同时有拥有很强的代码能力的人。同样是有所得必有所失，你平时习惯了去抄程序，必然少了很多自己构思程序的机会，从而影响代码能力的提高。
当然，我也不是完全反对去使用SCL，偶尔用一下也是可以的，例如在比赛中。但是，需要注意的是，一定要用自己整理的SCL。我见过有人拿着一本别人整理的SCL，虽然内容很齐整，但是我没见他用对过。因为这本SCL不是他整理的，他自己都不知道每个程序在使用的时候应该注意些什么，于是一用就错。

算法名言(含义深刻啊)

问题是这样的：问用n条直线最多能将平面分成多少个区域？ 
这也是一个很简单的递归问题： L[n] = L[n-1] + n;    (L[0] = 1)
    通项公式如下：L[n] = n * (n + 1) / 2 + 1     ( n>= 0 )

如果不用直线的话，用一个一般的折线，那么n个这样的折线最多可以拆分平面:
         D[n] = L[2*n] - 2 * n;
         D[n] = 2 * n ^ 2 - n + 1;

如果用"Z"字型的线，n个折线最可拆分平面：
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=652
         Z[n] = Z[n-1] + 9*n - 8;
         Z[n] = (9*n^2 - 7*n + 2) / 2;

1 #include<stdio.h>
2 int main()
3 {
4     int n;
5     while(scanf("%d",&n)!=EOF){
6         printf("%d\n",(9*n*n-7*n+2)/2);
7     }
8     return 0;
9 }

        每个符号三角形都是由它的第一行“+,-”号分布决定的，据此可演算出所有分布的三角形，对其进行统计即可。

        同时将一个n行三角形T的+，-号个数分别记为pos_num(n),neg_num(n)，其第一行中的+，-号个数记为x(n),y(n)，则可得到下式：

        pos_num(n)=x(n)+pos_num(n-1)

        neg_num(n)=y(n)+neg_num(n-1)

        由此，我们可以从n=1开始，利用前面n=k-1的结果，迭代求出n=k的分布情形，然后对n=k的所有分布统计。

题中，n<=24，时间空间均有限制，我们可以先求出所有结果，然后保存到数组直接取来输出。这是ACM题中很常见的情况。