Euler的任意四面体体积公式（已知边长求体积）

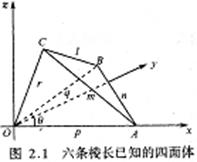
已知4点坐标求体积（其中四个点的坐标分别为（x1,y1,z1）,（x2,y2,z2）,（x3,y3,z3）,（x4,y4,z4）

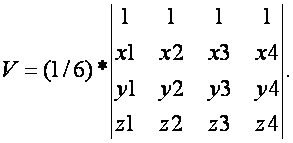
注意事项：

1. 注意舍入方式(0.5的舍入方向);防止输出-0.

2. 几何题注意多测试不对称数据.

3. 整数几何注意xmult和dmult是否会出界;

   符点几何注意eps的使用.

4. 避免使用斜率;注意除数是否会为0.

5. 公式一定要化简后再代入.

6. 判断同一个2*PI域内两角度差应该是

   abs(a1-a2)<beta||abs(a1-a2)>pi+pi-beta;

   相等应该是

   abs(a1-a2)<eps||abs(a1-a2)>pi+pi-eps;

7. 需要的话尽量使用atan2,注意:atan2(0,0)=0,

   atan2(1,0)=pi/2,atan2(-1,0)=-pi/2,atan2(0,1)=0,atan2(0,-1)=pi.

8. cross product = |u|*|v|*sin(a)

   dot product = |u|*|v|*cos(a)

9. (P1-P0)x(P2-P0)结果的意义:

   正: <P0,P1>在<P0,P2>顺时针(0,pi)内

   负: <P0,P1>在<P0,P2>逆时针(0,pi)内

   0 : <P0,P1>,<P0,P2>共线,夹角为0或pi