我编写的第一个JAVA程序，在Eclipse上成功运行！发博文表示庆贺，向Java处理大整数进发……
public class main{
public static void main(String[] args) {
System.out.println("Hello");
}
}
虽然Java里面有很多知识，目前对于我来说都是未知，但只要一步步努力，一点点进步，菜鸟起飞啦！
附上一篇文章：
JAVA大数处理(BigInteger,BigDecimal) 今日见了一个名词
SDK（Software Development Kit, 即软件开发工具包 ）
posted @
2010-10-07 21:08 孟起 阅读(210) |
评论 (0) |
编辑 收藏
把在n条线段中（以（0,0）为起点）放入m个点，使其等分为m+1份。
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3414
#include<stdio.h>
#include<math.h>
struct point
{
double x,y,len;
}p[1002];
int main()
{
int n,m,i,j,ca=1;
double ave,len,ax,ay;
while(scanf("%d%d",&n,&m)!=EOF)
{
p[0].x=0; p[0].y=0; ave=0;
for(i=1;i<=n;i++){
scanf("%lf%lf",&p[i].x,&p[i].y);
p[i].len=sqrt((p[i].x-p[i-1].x)*(p[i].x-p[i-1].x)+(p[i].y-p[i-1].y)*(p[i].y-p[i-1].y));
//printf("%.3f %.3f %.3f\n",p[i].x,p[i].y,p[i].len);
ave+=p[i].len;
}
ave/=(m+1); //每一份的均长
j=0; //沿着线段走
// printf("%.3f\n",ave);
printf("Route %d\n",ca++);
for(i=1;i<=m;i++)
{
len=0;
for(; j<n;j++)
{
if(len+p[j+1].len>ave)
break;
len+=p[j+1].len;
}
double res=ave-len;
//printf("%d %.3f\n",j,res);
ax=p[j].x+(res/p[j+1].len)*(p[j+1].x-p[j].x);
ay=p[j].y+(res/p[j+1].len)*(p[j+1].y-p[j].y);
printf("CP%d: (%.3lf, %.3lf)\n",i,ax,ay);
p[j].x=ax; p[j].y=ay;
p[j+1].len=sqrt((p[j+1].x-p[j].x)*(p[j+1].x-p[j].x)+(p[j+1].y-p[j].y)*(p[j+1].y-p[j].y));
}
}
return 0;
}posted @
2010-10-07 18:25 孟起 阅读(346) |
评论 (0) |
编辑 收藏一个环形的圈怎样用最少次数把它从顺时针变成逆时针（只能相邻位置交换位置）
一个环形，最优结果是把这个环分成 相差 最少的2部分，这2部分按照直线来求出结果再求和
直线如果把1234 换成4321
是冒泡的次数。。首先4123（3）+4312（2）+4321（1）=6
本题是把n看成两个 n/2 ，然后求出进行反序（冒泡）的次数
#include <stdio.h>
int main()
{
int n,t,r;
while(scanf("%d",&n)!=EOF)
{
t=n/2; r=n-t;
printf("%d\n",t*(t-1)/2+r*(r-1)/2);
}
return 0;
}
posted @
2010-10-07 10:10 孟起 阅读(722) |
评论 (0) |
编辑 收藏解决一个问题通常有多种方法， 我们总想找到最高效的，所以需要对比不同算法执行所用的时间。可惜的是，C++中提供的方法一般只能精确到毫秒级。
提供一种更加精确的方法。编写一个函数，可以在C++中这样写：
__declspec (naked) unsigned __int64 GetCpuCycle( void )
{
_asm
{
rdtsc
ret
}
}
RDTSC的返回值存放在EDX EAX中， EDX为高32位，EAX为低32位。这里的 RDTSC 指令( Read Time Stamp Counter )， 获得CPU的高精度时间戳。
这样以来我们就可以在随处获得当前的CPU自上电以来的时间周期数了：
unsigned __int64 iCpuCycle = GetCpuCycle();
根据这个数字我们可以计算出上电以来所经历的时间( 秒s )：
second = iCpuCycle / CPU主频率( HZ );
1GHZ = 1,000 MHZ = 1,000,000 KHZ = 1,000,000,000 HZ;
获取两次作差就可以得到运行的时间了。其实没必要换算成时间，关注差值就行了。
PS：
可以放心一个unsigned __int64 不会溢出 - - 可以计算一下你的CPU能保存多少年的时间。。
根据这一方法有几个好处： 一是精度高，二是函数调用开销最小，三是平台限制小，四是具有和CPU主频相对应的直接关系。。。 但是由于精度高，得到的数字浮动比较大。。
posted @
2010-10-06 21:39 孟起 阅读(651) |
评论 (0) |
编辑 收藏A triangle field is numbered with successive integers in the way shown on the picture below.
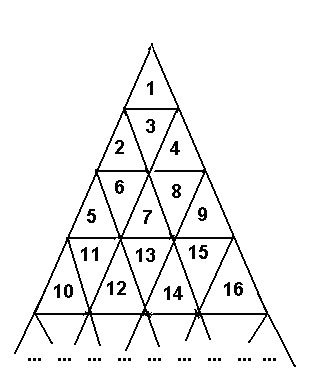
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
#include <stdio.h>
#include<math.h>
int main()
{
int temp,n,m,s,flag=3,cn,cm,zb,yb,cc,k,sj;
while(scanf("%d%d",&m,&n)==2 )
{
flag=3; s=0; k=0;
if(m>n)
{
temp=m; m=n; n=temp;
}
cn=(int)ceil(sqrt(n)); //判断n和m所在层数
cm=(int)ceil(sqrt(m));
cc=abs(cn-cm); //判断两点层差
zb=m+(cn-1)*(cn-1)-(cm-1)*(cm-1); //判断m辐射到n层所及范围的左边界和右边界
yb=zb+2*cc;
if(n>=zb && n <=yb) //判断n在m范围所须步数
{
s=2*(cc);
k=1;
}
else
{
if(n<zb) //判断n到m边界及m点所须步数和
s=2*(cc)+abs(n-zb);
else
s=2*(cc)+abs(n-yb);
}
sj=m-(cm-1)*(cm-1); //判断三角类型0正,1倒
if(abs(n-m)% 2 !=(cc) % 2)
{
if(sj % 2 ==1 )
flag=1;
else
flag=0;
}
if(flag==1 && k==1)
s=s-1; //假如n点在m点辐射范围内,正三角-1,倒三角+1,不在不判断.
if(flag==0 && k==1)
s=s+1;
printf("%d\n",s);
}
return 0;
}
cn-1)*(cn-1)是1到n-1行末尾的数，也就是1-n的里面小三角形的个数~，
(cm-1)*(cm-1);也是一样的嘛~
两个相减就是m行的个数了！~ m加个数不就是左边界了嘛~
zb+两倍的行差就是右边界了！~
而且正三角所到的边界是正三角型，反三角所到的边界是反三角型，这点要注意！
posted @
2010-10-06 18:05 孟起 阅读(1302) |
评论 (1) |
编辑 收藏http://acm.hdu.edu.cn/showproblem.php?pid=1875
Kruscal最小生成树 注意对double类型的快排可不要写错了
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
struct road{
int x,y;
double v;
}r[5002];
struct point{
int a,b;
}p[102];
int cmp(const void *a,const void *b)
{
struct road *aa=(struct road *)a;
struct road *bb=(struct road *)b;
return aa->v > bb->v ? 1:-1;
}
int bin[102];
int find(int x)
{
int r=x;
while(bin[r]!=r)
r=bin[r];
int y=x;
while(bin[y]!=y)
{
y=bin[y];
bin[y]=r;
}
return r;
}
int main()
{
int t,n,i,j,num,cnt;
double ans;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d%d",&p[i].a,&p[i].b);
num=0;
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++){
r[num].x=i, r[num].y=j;
r[num].v=sqrt(1.0*(p[i].a-p[j].a)*(p[i].a-p[j].a)+(p[i].b-p[j].b)*(p[i].b-p[j].b));
num++;
}
for(i=0;i<n;i++)
bin[i]=i;
qsort(r,num,sizeof(r[0]),cmp);
i=0; ans=0; cnt=0;
while(r[i].v<10)
i++;
for(;i<num && cnt<n-1;i++)
{
if(r[i].v>1000) break;
int fx=find(r[i].x), fy=find(r[i].y);
if(fx!=fy)
{
bin[fx]=fy;
cnt++;
ans+=r[i].v;
}
}
if(cnt==n-1)
printf("%.1lf\n",ans*100);
else
printf("oh!\n");
}
return 0;
}
posted @
2010-10-06 10:26 孟起 阅读(571) |
评论 (0) |
编辑 收藏
最简单的dijkstra应用，别的就不说了 题目链接：
http://acm.hdu.edu.cn/showproblem.php?pid=1874
#include<stdio.h>
#include<string.h>
#define MAXN 201
#define MAX 999999
int dist[MAXN][MAXN],x[MAXN];
int main()
{
int n,m,i,j,t,s,d,a,b,time,min;
while(scanf("%d%d",&n,&m)==2)
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if(i==j)
dist[i][j]=0;
else
dist[i][j]=MAX;
}
}
for(i=0;i<m;i++)
{
scanf("%d%d%d",&a,&b,&time);
dist[a][b]=dist[b][a]=time<dist[a][b]?time:dist[a][b];
}
scanf("%d%d",&s,&d);
for(i=0;i<n;i++)
x[i]=dist[s][i];
dist[s][s]=1;
t=0;
while(t!=-1)
{
min=-1;
t=-1;
for(i=0;i<n;i++)
if(dist[i][i]==0&&(min==-1||x[i]<min))
{
min=x[i];
t=i;
}
if(t!=-1)
{
dist[t][t]=1;
for(i=0;i<n;i++)
if(x[i]>x[t]+dist[t][i])
{
x[i]=x[t]+dist[t][i];
}
}
}
if(x[d]<MAX)
printf("%d\n",x[d]);
else
printf("-1\n");
}
return 0;
}
posted @
2010-10-06 09:23 孟起 阅读(519) |
评论 (0) |
编辑 收藏
思路如下，只要房子的号码是个完全平方数就可以逃跑了。
为什么呢？？？
因为完全平方数比方是25，只能分解为1，5，25，这三个数，以1代表门开了，0代表关了，则此时的序列就是1，0，1，
所以只要对输入的数求下平方根就好了。
换句话说在区间[1,n]中能整除n的数的个数，当n是平方数是奇数个，否则是偶数个。
http://acm.hdu.edu.cn/showproblem.php?pid=1337
#include<stdio.h>
#include<math.h>
int main()
{
int n,a;
scanf("%d",&n);
while(n--)
{
scanf("%d",&a);
printf("%d\n",(int)sqrt(a*1.0));
}
return 0;
}
posted @
2010-10-05 20:07 孟起 阅读(580) |
评论 (0) |
编辑 收藏在一无限大的二维平面中，我们做如下假设：
1、 每次只能移动一格；
2、 不能向后走（假设你的目的地是“向上”，那么你可以向左走，可以向右走，也可以向上走，但是不可以向下走）；
3、 走过的格子立即塌陷无法再走第二次；
求走n步不同的方案数（2种走法只要有一步不一样，即被认为是不同的方案）。
http://acm.hdu.edu.cn/showproblem.php?pid=2563
1 /*设a[n]是向上走n步的方法数，b[n]是向左或向右走的方法数，
2 则a[n]=a[n-1]+b[n-1], b[n]=２*a[n-1]+b[n-1]
3 因为f[n]=a[n]+b[n]
4 化简得f[n]=3*a[n-1]+2*b[n-2]=2*f[n-1]+a[n-1]=2*f[n-1]+f[n-2]
5 */
6 #include<stdio.h>
7 int main()
8 {
9 int i,t,n,f[22];
10 f[1]=3; f[2]=7;
11 for(i=3;i<=20;i++)
12 f[i]=2*f[i-1]+f[i-2];
13 scanf("%d",&t);
14 while(t--)
15 {
16 scanf("%d",&n);
17 printf("%d\n",f[n]);
18 }
19 return 0;
20 }
posted @
2010-10-05 11:54 孟起 阅读(623) |
评论 (0) |
编辑 收藏