《Near Optimal Hierarchical Path-Finding》中提出了一种层次A*算法，正好能够用于解决项目大地图寻路的问题。大致思路是：1）预处理。将地图划分为nxn大小的区块，找出每个区块与周围四个区块在边界上的互通点，在区块中使用局部A*对找出的点做连通性测试并将其保存下来；2）寻路时，使用预处理得到的数据（边界上的可通点与区块内部的互通点），先在区块层级上做一次A*，根据结果再在每个区块中使用局部A*找到区块与区块之间的路径，最终得到完整路径。
一、A* Path-Finding
A*算法就不多讲了，可参考：
A*算法的优化可从搜索节点储存和OpenList排序两方面入手。
二、预处理
每个相邻区块（C1和C2）都有一条由公共边，该边两侧小格组成L1和L2，则连通点集E满足下列条件：
- E ⊂ L1 ∪ L2
- ∀t ∈ L1 ∪ L2 : t ∈ E ⇔ symm(t) ∈ E ，其中symm(t)为对称关系
- E不含不可行走格子
对在E中且同边的连续格子取其中点，如下图所示：
_thumb.png "Image(6)")
对上面得到的位于同一区块的点集合使用local A*做连通性测试，下图用直线连接来表示两点互通：
_thumb.png "Image(7)")
三、寻路
使用区块连通信息，进行区块级A*，得到区块之间的连接点，如果在预处理时保存了区块内互通点的路径，就不必再进行区块内的local A*了。
实验结果表明，在未采用区块内预存路径的情况下，中长距离寻路使用层次A*后的平均效率是普通A*的5倍以上，距离越长效率对比越明显。
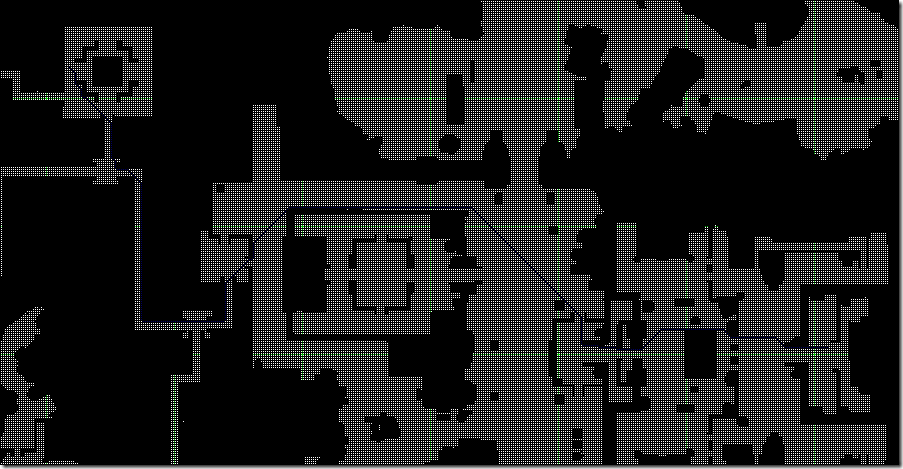
A* 93ms
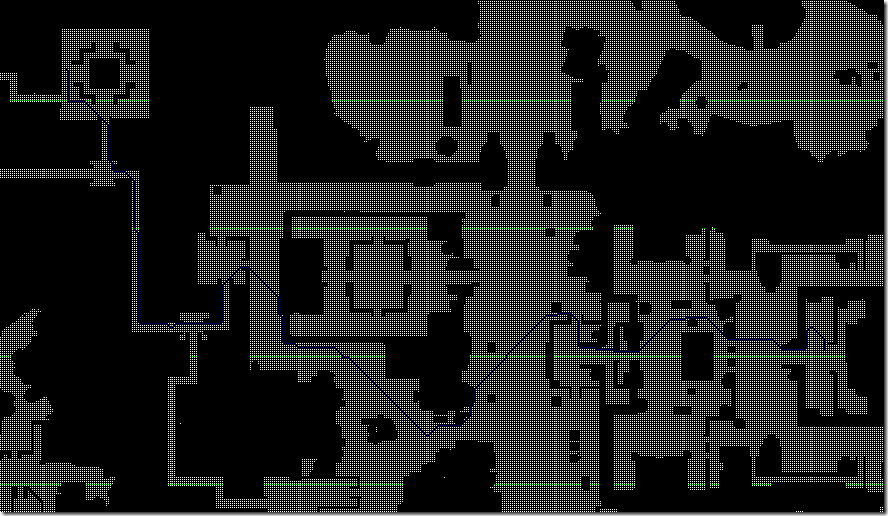
HPA* 15ms
从上图中可以看出，HPA*得到的路径并不是最优的，它是在最优和效率上的折中，适合作为长距离寻路的一种优化方案。
四、优化点
- 可扩展为多层而不仅限于一层
- 预存区块内连通点路径
- 区块边界可通面积较大时，产生不自然路径，如下图所示：
一个改进的方法是对过长的边界再做划分：
_thumb.png "Image(5)")