Prime Distance
|
简单刷表
|
| Yahtzee |
DP |
| Request for Proposal |
简单题 |
| Australian Voting |
模拟 |
| Chocolate Chip Cookies |
geometry |
Prime Distance
题目大意就是给你一个区间[l,r],找出这里相邻素数的最大距离和最小距离
刷表是经典而实用的方法Yahtzee
给十三种5个骰子的状态,十三种规则,每种规则下每个状态有一个得分,问怎样分配规则与状态之间的对应关系,让得分最大,同时要注意的是如果前六种规则下的得分如果>=63,那么总得分要加上35!
首先预处理出每种规则下每个状态的得分情况!
如果没有最后一个限制,那么我们可以有两种做法:1,二分图的最大权匹配;2,DP!但是有了最后一个限制,用匹配的话不知怎么下手,我只能想到dp!dp[i][j][k]表示前i种骰子状态已经分配好,分配的情况压缩成一个整数j,并且前六种规则的得分是k的状态,那么状态转移就是 dp[i][j][k] = {max(dp[ i - 1 ][ j - (1<<h) ][ k - score[h][i] ] ) (0<=h<=6),max(max(dp[ i - 1 ][ j - (1<<h) ][ k ])( 7<=h<13) } (j的第h位为1) ! 复杂度大概是13*2^13*64 ; 中间记录前一个状态, 最后递归输出就好了~
Request for Proposal:
Australian Voting:
按照题意模拟就好了~
Chocolate Chip Cookies
题目大意就是有一些点(200个), 用一个给定半径(r==5cm)的圆,最多能罩住多少个点
200个点的话 o ( n^3 )能过,这样我们有了算法,要罩住最多的点,那个圆必须至少要
卡住两个点
枚举每两个点确定圆心,在检查所有的点是否在圆内。想法很自然
细节问题上就是如何找到圆心(确定半径和两个圆上的点)
这是基本功 如果说直接解方程有些繁琐这里有好方法:
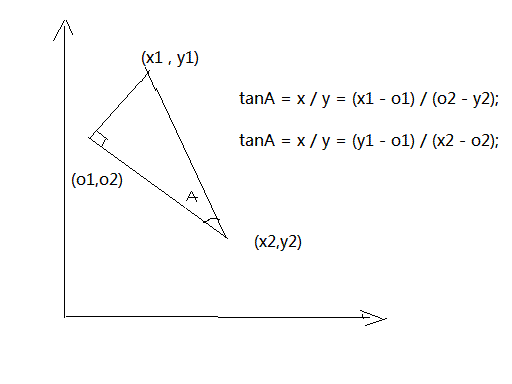
这样只要解二元一次方程,可参考以下代码:
1 struct point {double x, y;};
2
3 bool centre(point p, point q, double r,point &o1, point &o2)
4 //两点一半径会确定两个圆心 o1 o2
5 {
6 double rise,run,theta;
7 double chordlen, perplen;
8 double tantheta,tantheta1;
9
10 chordlen = sqrt( (p.x-q.x)*(p.x-q.x) + (p.y-q.y)*(p.y-q.y) );
11 if (chordlen > 2*r) { return false; }
12 tantheta = sqrt(r*r*4 - chordlen*chordlen)/(chordlen);
13 //圆心角<poq的半角的正切值
14
15 run = (p.x-q.x)/2;
16 rise = (p.y-q.y)/2;
17 o1.x= (p.x+q.x)/2 + rise * tantheta;
18 o1.y= (p.y+q.y)/2 + -run * tantheta;
19 o2.x= (p.x+q.x)/2 + -rise * tantheta;
20 o2.y = (p.y+q.y)/2 + run * tantheta;
21 //结合点积就能得出上式
22 return true;
23 }
24