学习normal mapping时，首先需要理解什么是TBN矩阵，在http://blog.csdn.net/soilwork/archive/2006/12/30/1468860.aspx中的环形图已经可以很容易理解TBN的三个分量含义了，但是对于如何计算，找了很多地方都没有一个比较“通俗”的算法（实际上是我没有看懂...）
这里介绍一种本人想到的最容易看懂的算法，不过计算量还是比较大呵呵





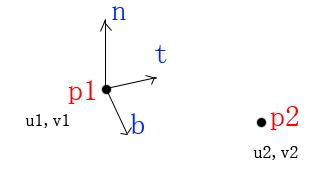
如图，已知2个点，坐标分别是P1，P2，还已知他们的纹理坐标，分别是（u1，v1）和（u2，v2），还知道了第一个点的法向量，我们要计算的就是P1的tangent space，即除了法向量外的所谓的“副法向量”B 和所谓的“tangent向量”T。

直接假设所求的B和T在世界坐标中的值：B=（xb，yb，zb），T=（xt，yt，zt）

很容易就知道：
T·B=0
N·T=0
B·N=0
另外他们都是单位向量，又有：
|T|=1
|B|=1
接下来，我们可以用点1的各个数据来表示点2的坐标位置：

P1+T*（u2-u1）+B*（v2-v1）=P2（或者uv交换位置：P1+T*（v2-v1）+B*（u2-u1）=P2，具体是那个可以不管...）


这样6个未知量6个方程，就可以计算得出点1的tangent space了~~

从这里也可以理解到，当纹理贴图坐标不够连续时为什么normal mapping的效果会不理想，因为计算一个点的tangent space还要依赖周围的点的信息