A Knight's Journey
| Time Limit: 1000MS |
|
Memory Limit: 65536K |
| Total Submissions: 18085 |
|
Accepted: 6095 |
Description
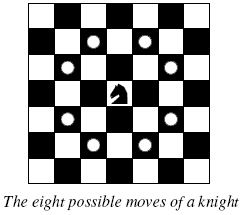
Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
Sample Input
3
1 1
2 3
4 3
Sample Output
Scenario #1:
A1
Scenario #2:
impossible
Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4
这个题目要求给出遍历棋盘的字典序，所以要给扩展一个顺序，我也不明白为什么这样是字典序
dx[8][2]={{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}};
这个搜索顺序总是先找字母数字小的，即以左上角为原点，当前为（i,j）总是找比先找比该点行或列小的，在找行或列大的，
行列中总是先找行
这里的行要按字母顺序，列要按数字顺序，样例很纠结、
如果是存在能遍历棋盘上所有点的解的话，那从棋盘上任意一点出发总能遍历棋盘上所有的点，、
这里要 1
#include<stdio.h>
2#include<string.h>
3#include<math.h>
4
int dx[8][2]=
{{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}};
5int stack[100][2];
6int n,m,tot;
7int mark[27][27];
8short flag;
9void print()
10{
11
int i;
12 for (i=1;i<=tot ;i++ )
13
{
14 printf("%c%d",stack[i][0]+64,stack[i][1]);
15
}
16 printf("\n");
17
}
18void dfs(int num)
19{
20 int i,xn,yn,x,y,numn;
21 if (num==tot&&!flag)
22 {
23 print();
24 flag=1;
25 return;
26 }
27 x=stack[num][0];
28 y=stack[num][1];
29 for (i=0;i<8 ;i++ )
30 if (flag==0)
31 {
32 xn=x+dx[i][0];
33 yn=y+dx[i][1];
34 if ((xn>0)&&(xn<=n)&&(yn>0)&&(yn<=m)&&(mark[xn][yn]==0))
35 {
36 numn=num+1;
37 mark[xn][yn]=1;
38 stack[numn][0]=xn;stack[numn][1]=yn;
39 dfs(numn);
40 mark[xn][yn]=0;
41 }
42 }
43 else return;
44}
45int main()
46{
47 int t,i;
48 scanf("%d",&t);
49 for (i=1;i<=t ;i++ )
50 {
51 scanf("%d%d",&m,&n);
52 memset(mark,0,sizeof(mark));
53 memset(stack,0,sizeof(stack));
54 mark[1][1]=1;
55 tot=n*m;
56 flag=0;
57 stack[1][0]=1;
58 stack[1][1]=1;
59 printf("Scenario #%d:\n",i);
60 dfs(1);
61 if (!flag)
62 {
63 printf("impossible\n");
64 }
65 //if (i!=t)
66 {
67 printf("\n");
68 }
69 }
70 return 0;
71}
72 求字典序
所以应从（1，1）开始遍历