这题其实是一个树状数组的思维转换题，一般来说我们是该一个点，求一段和(对于一维的)。但是如果出现下面情况，你会如何处理？(借用TC里介绍树状数组的那个大哥的,链接在我上一篇树状数组文章里)
There is an array of n cards. Each card is putted face down on table. You have two queries:
1. T i j (turn cards from index i to index j, include i-th and j-th card - card which was face down will be face up; card which was face up will be face down)
2. Q i (answer 0 if i-th card is face down else answer 1)
这里是更新一段，但是只求一点，和我们一般的思路不一样，但是不打紧，我们可以改变思维，我们可以这样想(引用)
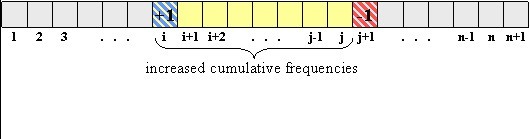
This has solution for each query (and 1 and 2) has time complexity O(log n). In array f (of length n + 1)we will
store each query T (i , j) - we set f[i]++ and f[j + 1]--. For each card k between i and j (include i and j)
sum f[1] + f[2] + ... + f[k] will be increased for 1, for all others will be same as before
(look at the image 2.0 for clarification), so our solution will be described sum
(which is same as cumulative frequency) module 2.
看了这之后，是不是发现原来还可以这样啊，呵呵，这就是思维转换了，如果你已经知道这中思路了，那么这篇文章基本不用看了，因为你已经会
好了，接下来我们说说POJ这题吧，你是不是发现这题和上面那个英文描述的题很像呢，只不过这个是二维的，恩，确实，其实上面那个就是
POJ_2155的一维版本，好了这样说，你应该懂了吧。下面看看代码吧(建议先自己想哦)，再提供篇集训论文吧
CODE
1/**//*
2
ID:Klion
3 PROG:POJ_2155
4 LANG:C++
5
*/
6
#include <iostream>
7using namespace std;
8int n;
9int num[1002][1002];
10void update(int x,int y)
11
{//这里确实很帅啊
12 int y1;
13 while(x <= n)
14
{
15 y1 = y;
16 while(y1 <= n)
17 {
18 num[x][y1] ^= 1;
19 y1 += (y1 & -y1);
20
}
21 x += (x & -x);
22 }
23}
24void work(int x1,int y1,int x2,int y2)
25{//主要是这里，好好想清楚
26 update(x1,y1);
27 update(x2+1,y1);
28 update(x1,y2+1);
29 update(x2+1,y2+1);
30}
31int read(int x,int y)
32{
33 int ret=0;
34 int y1;
35 while(x > 0)
36 {
37 y1 = y;
38 while(y1 > 0)
39 {
40 ret = ((ret + num[x][y1]) & 1);
41 y1 -= (y1 & -y1);
42 }
43 x -= (x & -x);
44 }
45 ret &= 1;
46 return ret;
47}
48int main(void)
49{
50 freopen("POJ_2155.in","r",stdin);
51 freopen("POJ_2155.out","w",stdout);
52 int t;
53 int x1,y1,x2,y2;
54 int x,y;
55 int l;
56 char str[2];
57 scanf("%d",&t);
58 while(t--)
59 {
60 memset(num,0,sizeof(num));
61 scanf("%d%d%*c",&n,&l);
62 for(int i = 0;i < l;i++)
63 {
64 scanf("%s",str);
65 if('Q' == str[0])
66 {
67 scanf("%d%d%*c",&x,&y);
68 printf("%d\n",read(x,y));
69 }
70 else
71 {
72 scanf("%d%d%d%d%*c",&x1,&y1,&x2,&y2);
73 work(x1,y1,x2,y2);
74 }
75 }
76 printf("\n");
77 }
78 return 0;
79}
80