题意
一开始想到用二维线段树,但是我没写过二维的,只写过一维的。后来问了下别人,说一维也行(一开始我也想到是不是可以用一维的,但是很快就被我自己给否定了,我认为那样时间会不够的,后来再第11个点还真的不够)。于是就写了一个一维的线段树。把每一行进行一次线段树操作。这样空间也可以开出来,变成复杂度也不高。可是交上去之后在第11个点超时了。给的是2S,我的运行了2.67S。有人说可以从后往前染色,那样的话,如果某个区域已经染色了,那么后面就不用在染色了,因为在染色是没有意义的。无奈不会实现,想着用并查集稍微加速下,可是发现不怎么好合并(哪位高人看了给指点指点,看到一牛人写了点,不过由于水平问题,实在不知并查集怎么实现这个问题的),于是一直TLE,今天看了nocow的题解,发现基本是用矩形切割做的.推荐看薛茅的论文,开始对这个东西我还一无所知。终于在那看到个线段树的,第11组数据也只有0.7S。后来看了下,发现那个程序也是用一维的线段树搞的,不过比我的实现的好,首先不是每一行都进行一次线段树操作,那样时间肯定是不够的。我们来看下面这幅图,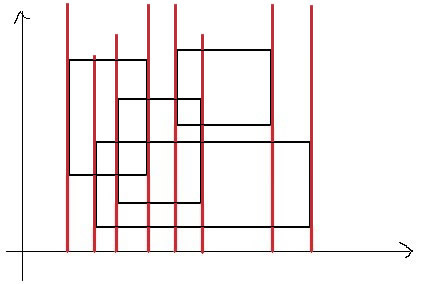
图中的黑色框是原矩形,红色的是我们投影的那些值(这里没有画大矩形的两条边)。
我们首先对垂直X轴的边投影(其中包括原来大矩形的两条边),得到一些列的值,那么以后只要对这些值中相邻的两个之间(图中的红色线条之间的区域)进行一次线段树的操作这样的话可以减少不少的操作,也就是说原来的一行进行一次,可以把某些行进行合并,因为这些行(每两条相邻的红色线段之间的行)的颜色都一样的。这样操作之后最大一组数据用时0.7S.
似乎这题的标准解法是矩形切割。到时再去看看。
下面再看看矩形切割的方法。(代码不是我的。官方的,我只加了点注释)
直接上代码
下面的一个图贴在代码里面会乱,在这贴下吧(我无语了,还是会乱,只好截图了)
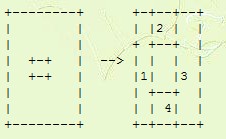
  CODE CODE
1 #include <stdio.h> #include <stdio.h>
2 #include <stdlib.h> #include <stdlib.h>
3 #include <string.h> #include <string.h>
4
5  FILE *fp,*fo;/**//*输入输出文件*/ FILE *fp,*fo;/**//*输入输出文件*/
6
7 struct rect struct rect
8   {/**//*矩形结构体*/ {/**//*矩形结构体*/
9 int c; int c;
10 int x1,y1,x2,y2; int x1,y1,x2,y2;
11 }; };
12
13  int c[2501];/**//*颜色的多少*/ int c[2501];/**//*颜色的多少*/
14 rect r[10001]; rect r[10001];
15
16 int intersect(rect a,const rect &b,rect out[4]) int intersect(rect a,const rect &b,rect out[4])
17   { {
18  /**//* do they at all intersect? */ /**//* do they at all intersect? */
19 if(b.x2<a.x1||b.x1>=a.x2) if(b.x2<a.x1||b.x1>=a.x2)
20 return 0; return 0;
21 if(b.y2<a.y1||b.y1>=a.y2) if(b.y2<a.y1||b.y1>=a.y2)
22 return 0; return 0;
23  /**//*上面表示不相交*/ /**//*上面表示不相交*/
24  /**//* they do */ /**//* they do */
25
26 rect t; rect t;
27
28 if(b.x1<=a.x1&&b.x2>=a.x2&&b.y1<=a.y1&&b.y2>=a.y2) if(b.x1<=a.x1&&b.x2>=a.x2&&b.y1<=a.y1&&b.y2>=a.y2)
29  return -1; /**//*全部覆盖前面的某个矩形*/ return -1; /**//*全部覆盖前面的某个矩形*/
30
31  /**//* cutting `a' down to match b */ /**//* cutting `a' down to match b */
32  /**//*********************** /**//***********************
33 +--------+ +-+--+--+ +--------+ +-+--+--+
34 | | | |2 | | | | | |2 | |
35 | | + +--+ | | | + +--+ |
36 | +-+ | --> | | | | | +-+ | --> | | | |
37 | +-+ | |1 | |3 | | +-+ | |1 | |3 |
38 | | | +--+ | | | | +--+ |
39 | | | | 4 | | | | | | 4 | |
40 +--------+ +-+--+--+ +--------+ +-+--+--+
41 ***********************/ ***********************/
42  int nout=0;/**//*记录分成多少块*/ int nout=0;/**//*记录分成多少块*/
43  if(b.x1>=a.x1) if(b.x1>=a.x1)  {/**//*上右图中的1*/ {/**//*上右图中的1*/
44 t=a,t.x2=b.x1; t=a,t.x2=b.x1;
45 if(t.x1!=t.x2) if(t.x1!=t.x2)
46 out[nout++]=t; out[nout++]=t;
47 a.x1=b.x1; a.x1=b.x1;
48 } }
49  if(b.x2<a.x2) if(b.x2<a.x2)  {/**//*上右图中的3*/ {/**//*上右图中的3*/
50 t=a,t.x1=b.x2; t=a,t.x1=b.x2;
51 if(t.x1!=t.x2) if(t.x1!=t.x2)
52 out[nout++]=t; out[nout++]=t;
53 a.x2=b.x2; a.x2=b.x2;
54 } }
55  if(b.y1>=a.y1) if(b.y1>=a.y1)  {/**//*上右图中的4*/ {/**//*上右图中的4*/
56 t=a,t.y2=b.y1; t=a,t.y2=b.y1;
57 if(t.y1!=t.y2) if(t.y1!=t.y2)
58 out[nout++]=t; out[nout++]=t;
59 a.y1=b.y1; a.y1=b.y1;
60 } }
61  if(b.y2<a.y2) if(b.y2<a.y2)  {/**//*上右图中的2*/ {/**//*上右图中的2*/
62 t=a,t.y1=b.y2; t=a,t.y1=b.y2;
63 if(t.y1!=t.y2) if(t.y1!=t.y2)
64 out[nout++]=t; out[nout++]=t;
65 a.y2=b.y2; a.y2=b.y2;
66 } }
67 return nout; return nout;
68 } }
69
70  int main(void) int main(void)  { {
71 fp=fopen("rect1.in","rt"); fp=fopen("rect1.in","rt");
72 fo=fopen("rect1.out","wt"); fo=fopen("rect1.out","wt");
73
74 int a,b,n; int a,b,n;
75 fscanf(fp,"%d %d %d",&a,&b,&n); fscanf(fp,"%d %d %d",&a,&b,&n);
76  /**//*把原始矩形加进去*/ /**//*把原始矩形加进去*/
77 r[0].c=1; r[0].c=1;
78 r[0].x1=r[0].y1=0; r[0].x1=r[0].y1=0;
79 r[0].x2=a; r[0].x2=a;
80 r[0].y2=b; r[0].y2=b;
81
82 rect t[4]; rect t[4];
83
84 int i,j,rr=1; int i,j,rr=1;
85 for(i=0;i<n;i++) for(i=0;i<n;i++)
86   { {
87 int tmp; int tmp;
88 fscanf(fp,"%d %d %d %d %d",&r[rr].x1,&r[rr].y1,&r[rr].x2,&r[rr].y2,&r[rr].c); fscanf(fp,"%d %d %d %d %d",&r[rr].x1,&r[rr].y1,&r[rr].x2,&r[rr].y2,&r[rr].c);
89
90 if(r[rr].x1>r[rr].x2) if(r[rr].x1>r[rr].x2)
91   { {
92 tmp=r[rr].x1; tmp=r[rr].x1;
93 r[rr].x1=r[rr].x2; r[rr].x1=r[rr].x2;
94 r[rr].x2=tmp; r[rr].x2=tmp;
95 } }
96 if(r[rr].y1>r[rr].y2) if(r[rr].y1>r[rr].y2)
97   { {
98 tmp=r[rr].y1; tmp=r[rr].y1;
99 r[rr].y1=r[rr].y2; r[rr].y1=r[rr].y2;
100 r[rr].y2=tmp; r[rr].y2=tmp;
101 } }
102
103 int nr=rr; int nr=rr;
104 rect curr=r[rr++]; rect curr=r[rr++];
105 for(j=0;j<nr;j++) for(j=0;j<nr;j++)
106   { {
107 int n=intersect(r[j],curr,t); int n=intersect(r[j],curr,t);
108  if(!n)/**//*和r[j]不相交*/ if(!n)/**//*和r[j]不相交*/
109 continue; continue;
110 if(n==-1) if(n==-1)
111   {/**//*全部覆盖r[j]*/ {/**//*全部覆盖r[j]*/
112 memmove(r+j,r+j+1,sizeof(rect)*(rr-j-1)); memmove(r+j,r+j+1,sizeof(rect)*(rr-j-1));
113  /**//*把r数组从r[j+1]全部往前移一位*/ /**//*把r数组从r[j+1]全部往前移一位*/
114  j--;/**//*进行相应的调整*/ j--;/**//*进行相应的调整*/
115 rr--; rr--;
116 nr--; nr--;
117 continue; continue;
118 } }
119  r[j]=t[--n];/**//*分成几块*/ r[j]=t[--n];/**//*分成几块*/
120  for(;n-->0;)/**//*把分成的几块加进去*/ for(;n-->0;)/**//*把分成的几块加进去*/
121 r[rr++]=t[n]; r[rr++]=t[n];
122 } }
123 } }
124
125  for(i=0;i<rr;i++)/**//*现在每一块都是单一颜色的 直接统计*/ for(i=0;i<rr;i++)/**//*现在每一块都是单一颜色的 直接统计*/
126 c[r[i].c]+=(r[i].x2-r[i].x1)*(r[i].y2-r[i].y1); c[r[i].c]+=(r[i].x2-r[i].x1)*(r[i].y2-r[i].y1);
127
128 for(i=1;i<=2500;i++) for(i=1;i<=2500;i++)
129  if(c[i])/**//*输出*/ if(c[i])/**//*输出*/
130 fprintf(fo,"%d %d\n",i,c[i]); fprintf(fo,"%d %d\n",i,c[i]);
131
132 return 0; return 0;
133 } }
134

|
|
常用链接
留言簿(1)
随笔分类(99)
随笔档案(71)
好友链接
搜索
最新评论

阅读排行榜
评论排行榜
|
|