(当个日记记录Treap这一结构,详细参见http://www.nocow.cn/index.php/Treap, 在这里我着重讲一下旋转)
Treap,它其它就是一个二叉查找树(BST)+堆(HEAP). 它的数据有两个:关键值(key),优先级(fix).
用struct表示Treap的结点的结构如下:
struct node
{
datatype key;
int fix;
node * left;
node * right;
}
Treap的key值满足BST的性质:即任一个Treap的结点x,若y是x的左子树,则y.key<=x.key,若y为x的右子树,则y.key>=x.key.
同时Treap的fix满足Heap的性质(在这里以最大堆为例):即任一个Treap的结点x,若y为x的左子树或右子树,则x.fix>=y.fix.
如下图所示则为Treap

Treap的作用:它的作用同BST一样,引入优先级这一概念是为了防止BST退化成一链表(BST的建立依籁于结点的插入顺序,当有序的插入时,则BST为一链表,其它查找插入的复杂度o(n)),当然我们完全可以随机的插入结点,但是有时候我们事先并不知道所有结点,在这种情况下我们可以采用Treap,即当需要插入的一个新的key值,我们可以随机的生成一个优先级(fix),然后通过fix约束Treap,从而达到随机生成BST的目的.
为了插入和删除之后仍然保持Treap的两个性质,在这里Treap提供了两种旋转的操作,右旋和左旋
(1)结点右旋:node x,令y=x->left; 先将y的右子树作为x的左子树,然后将x作为y的右子树, 最后将y作为x原父结点的子树(原x为左子树,此时y仍然为左子树,x为右子树,y也为右子树)如下图所示.
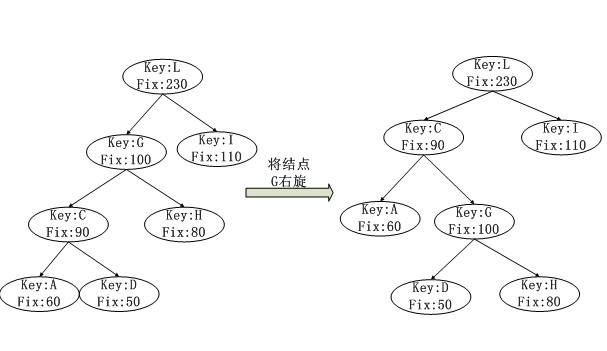
(2)结点左旋:同右旋刚好相反.node x,令y=x->right; 先将y的左子树作为x的右子树,然后将x作为y的左子树, 最后将y作为x原父结点的子树(原x为左子树,此时y仍然为左子树,x为右子树,y也为右子树)如下图所示.
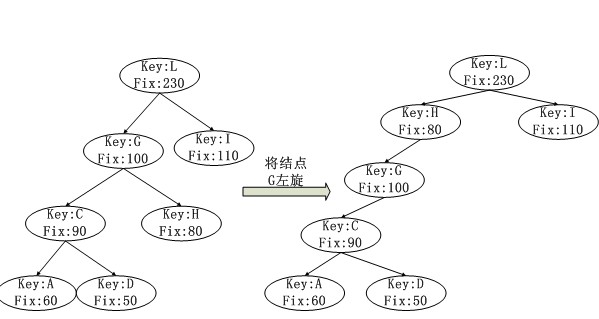
由上可见,旋转操作之后仍然满足BST的特性,但是改变Heap的性质.
插入操作:有了旋转操作后,插入变得十分简单.它只需要将结点(key,fix)按BST插入到Treap,此时若不满足Heap的性质,若结点x的左子树的fix大于x的fix,则只需要左旋,若结点y的右子树的fix值大于x的fix,则左旋.直至满足Heap的性质.
删除操作:只需要将删除的结点旋转至叶结点,直接插除即可.
对于其它的查找,后继,最小值等操作均同BST一样,在这里便不再详述.附有C++ Treap实现.
using std::ostream;
using std::endl;
using std::cout;
class Treap
{
private:
struct node
{
int key;
int fix;//priority,for heap
node * left,*right;//left child and right child
node(const int &_k):key(_k),left(NULL),right(NULL),fix(rand())
{
}
};
friend std::ostream & operator <<(std::ostream &os,node * const &r)
{
if(r==NULL)
return os;
os<<r->left;
os<<r->key<<std::endl;
os<<r->right;
return os;
}
inline void rol_l(node * &x)//rotate to left on node x
{
node * y=x->right;
x->right=y->left;
y->left=x;
x=y;
}
inline void rol_r(node * &x)//rotate to right on node x
{
node * y=x->left;
x->left=y->right;
y->right=x;
x=y;
}
void insert(node * & r,const int &key)
{
if(r==NULL)
{
r=new node(key);
}else
{
if(key<r->key)
{
insert(r->left,key);
if(r->left->fix>r->fix)
rol_r(r);
}else
{
insert(r->right,key);
if(r->right->fix>r->fix)
rol_l(r);
}
}
}
void remove(node * &r,const int &key)
{
if(r==NULL)
return;
if(key<r->key)
remove(r->left,key);
else if(key>r->key)
remove(r->right,key);
else
{
//remove node r
if(r->left==NULL && r->right==NULL)
{
delete r;
r=NULL;
}else if(r->left==NULL)
{
node * t=r;
r=r->right;
delete r;
}else if(r->right==NULL)
{
node * t=r;
r=r->left;
delete t;
}else
{
if(r->left->fix<r->right->fix)
{
rol_l(r);
remove(r->left,key);
}else
{
rol_r(r);
remove(r->right,key);
}
}
}
}
bool find(node * const & r,const int &key)
{
if(r==NULL)
return false;
if(r->key==key)
return true;
else
if(key<r->key)
return find(r->left,key);
else
return find(r->right,key);
}
void free(node * &r)
{
if(r==NULL)
return;
free(r->left);
free(r->right);
delete r;
r=NULL;
}
node * root;
public:
Treap():root(NULL)
{
}
~Treap()
{
free(root);
}
void insert(const int &key)
{
insert(root,key);
}
void remove(const int &key)
{
remove(root,key);
}
bool find(const int &key)
{
find(root,key);
}
friend std::ostream & operator <<(ostream & os,const Treap &t)
{
os<<t.root;
return os;
}
};
int main()
{
Treap t;
for(int i=0;i<10;i++)
t.insert(i);
std::cout<<t;
t.remove(3);
cout<<"after remove 3"<<endl;
std::cout<<t;
t.remove(5);
cout<<"after remove 5"<<endl;
std::cout<<t;
system("pause");
}
posted on 2009-08-12 21:57
kuramawzw 阅读(931)
评论(0) 编辑 收藏 引用 所属分类:
数据结构