永远也不完美的程序

不断学习，不断实践，不断的重构……

常用链接

统计

积分与排名

好友链接

最新评论

Frustum culling

by  Dion Picco

Introduction


I always amazed by the fact that most neophyte 3D engine programmers still do not realize the simple principal and benefits of frustum culling. I often frequent the forums on flipcode and I find that there are a ton of questions regarding this subject despite the plethora of information freely available. So I抳e decided to put together this simple document outlining my frustum culling procedures that I use in my current quad-tree culled engine. There are variations and perhaps much better ways of doing some of the culling techniques but the methods presented here should suffice for learning. Before I start I want to mention one thing. I previously have used the term frustrum but I was constantly beleaguered by the denizens of the forums for this incorrect moniker. As it turns out, frustum is the correct term. I apologize to anyone whom I抳e offended... you nit-picky twits.

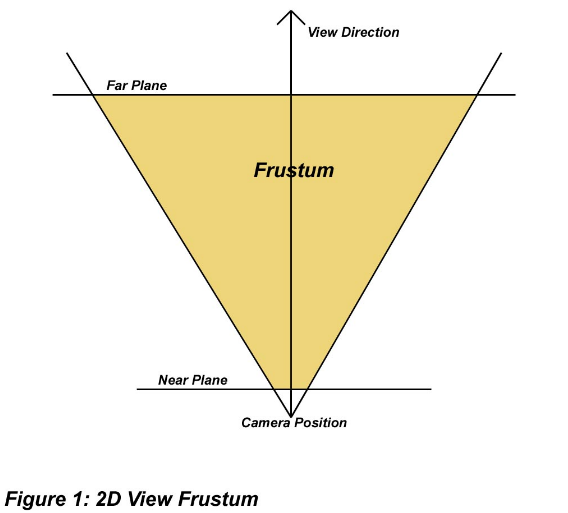
Most people already know what the viewing frustum is. For those who don抰, it抯 simply the area of your world visible to your current camera. The shape of the frustum is a pyramid with the nearest peak truncated at what is deemed the 憂ear?clipping plane (see Figure 1). In fact the frustum itself is (or can be) defined by 6 planes. These planes are named (surprise, surprise) the near plane, the far plane, the left plane, the right plane, the top plane and the bottom plane. Frustum culling is simply the process of determining whether or not objects are visible in this area. Since frustum culling is essentially a 3D world-space procedure, it can be processed long before we even deal with individual polygons in our pipeline. Hence, we can quickly reject on the object level, unlike backface culling for example which takes place much later in the rendering pipeline and works on a per-polygon basis. This means that we don抰 even have to send the data to the video card once the object is frustum culled which of course makes quite a difference in rendering speed. It is simply very, very fast to render nothing.



The maximum benefit of frustum culling comes from a hierarchy culling method. This means that our world is broken down into a tree-like structure. Once we cull a top level node, we don抰 have to cull lower level nodes since they cannot be visible anyway. This means that we don抰 frustum cull ALL the objects in our world. We simply process them in a hierarchal fashion, which greatly reduces the number of frustum culls. Without a hierarchal method, frustum culling still has a good advantage over not doing it at all but it also means that it scales linearly with the number of objects in our world. In other words, 100 objects require 100 frustum culls. 1,000,000 objects require 1,000,000 culls. At some point we end up spending so much time doing the culling anyway that we are not going to notice an increase in speed. In designing a fast game, we NEVER EVER want any of our algorithms working on a linear scale unless there are only 2 or 3 items to process or there is no better way of doing it. I refuse to accept the latter. This means that a hierarchal culling method is necessary. Consider the case where we have 100 objects, with only 1 visible, and we are going to cull them in a binary fashion (very simplistic for this example). Normally in a linear method, we would simply test every single object (all 100) and check whether or not they are visible. This of course results in 100 cull checks, although it抯 possible that we could encounter an early out. Now consider a binary case. In the first check we can reduce our number to 50... the next check reduces our number to 25... the next to 13... the next to 7... the next to 4... the next to 2 and finally to 1. Six checks in total! That抯 quite a far cry from the 100. And it gets much better relative to the linear method as the number of items increases. In fact in this case, the linear method has to check N items whereas the binary method has to only check log N items (log base 2). Type some numbers into a calculator and see the difference for yourself.

For this example I am going to use a quad-tree for my hierarchal culling method. An octree or binary tree or any other structure could be used. In fact, most of the code will easily carry over. I choose a quad-tree since it抯 inherently easy to visualize. A quad-tree is essentially a 2-dimensional area constructed using a tree structure where each node has 4 children (see Figure 2). In this case, the children each occupy one quarter of the area of the parent quad-tree. This can be defined then again (recursively) for each of the children nodes. What this then forms is a hierarchy where the children nodes are contained entirely within the parent node. When we decide the parent node isn抰 visible, we can safely assume that the child nodes are also not visible. By setting our world up this way we can quickly cull LARGE amounts of our world with just a simple few culling checks. This works great for a terrain engine for example. And it抯 extendable as well. We can add our trees or bushes or rocks into this quad-tree into the smallest nodes which they entirely fit. Then when we perform our hierarchal culling and determine that a node isn抰 visible, we can also assume that any objects (trees, rocks, etc) are also not visible. It becomes a beautiful system capable of handling large worlds with lots of objects and still running very fast. And to make the best of it, it抯 very simple!


Fundamental Methods 1


The first step in planning a system like this is making sure you have the basic methods of culling up and running. This means that we want to be able to construct the 6 planes of the frustum from our view/projection matrices as well as check whether a sphere is outside the frustum and whether a bounding box is outside the frustum. To be more concise, we want to know whether a sphere and box either is contained entirely within the frustum, entirely outside or intersecting the frustum. This will allow us to make more 憈weaks?to our hierarchal culling system later on. These are the methods we will look at in this section.

First let抯 try to define our frustum. The 6 planes of the frustum can be defined from the view/projection matrix which form our camera system in our rendering API. Constructing these are a bit different for Direct3D and OpenGL. I could try to explain both or even one but I would probably just confuse you more. Luckily a friend of mine wrote a great pdf covering this. I met Gil when I visited Raven Software back in 1996. I was actually hired by them to work with Gil but NAFTA regulations would not allow me to cross the border without a university degree. Damn you NAFTA! Damn you all to hell! But anyway, that抯 another story for another time. The important part is this great pdf document that very simply explains the process of extracting the planes from the matrices. I suggest you read this and understand it. Here is the link:

http://www2.ravensoft.com/users/ggribb/plane%20extraction.pdf

Now I assume that you have a frustum class built that simply contains the 6 planes that define it. Make sure that you reconstruct this frustum and store it in your camera class each time the view or projection matrix changes and NOT each time you perform an intersection test. Our next step is to determine whether or not a sphere is contained within the frustum, outside the frustum or intersecting the frustum. This is actually a very simple process and breaks down like this: Determine whether the sphere is on the front side of a plane, the back side of a plane or intersecting a plane?do this for all 6 planes. This process itself is very simple indeed. What we need to do is to calculate the distance from the center of the sphere to the plane. If the absolute value of the distance is less than the radius of the sphere, then we are intersecting the plane. If the distance is greater than 0 then we are on the front side of the plane (and possibly inside the frustum). If it is less than 0 we are on the backside of the plane and definitely outside the frustum. Calculating the distance from the center of the sphere to the plane is as follows:

C = center of sphere
N = normal of plane
D = distance of plane along normal from origin

Distance = DotProduct(C, N) + D

So like I said previously, all we need to do now is to compare this distance to the radius of the sphere to determine the status of the intersection of the sphere in regards to the frustum. Here is the code that I use to perform this action:


                        // tests if a sphere is within the frustrum
                        int Frustrum::ContainsSphere(const Sphere& refSphere) const
                        {
                        // various distances
                        	float fDistance;

	// calculate our distances to each of the planes
                        	for(int i = 0; i < 6; ++i) {

		// find the distance to this plane
                        		fDistance = m_plane[i].Normal().dotProduct(refSphere.Center())+m_plane[i].Distance();

		// if this distance is < -sphere.radius, we are outside
                        		if(fDistance < -refSphere.Radius())
                        return(OUT);

		// else if the distance is between +- radius, then we intersect
                        		if((float)fabs(fDistance) < refSphere.Radius())
                        return(INTERSECT);
                        }

	// otherwise we are fully in view
                        	return(IN);
                        }


Our next step is to determine (in the case of a quad-tree) the status of an axis-aligned bounding box in regards to the frustum. There are a few ways of going about this operation. In this case I simply define my bounding box as a series of 3 minimum values and 3 maximum values and then compare all 8 vertices of the box against the frustum. While this isn抰 the quickest way, it is certainly the easiest for the beginner to understand. The method for doing this is to test each and every vertex (corner) of the box against the frustum to see where they lie in relation to it. If all the points are inside the frustum, then the box is fully contained. If at least 1 point is inside the box but not all of them, then it intersects the frustum. If all the points are on the backside of a particular plane, then the box is outside. Otherwise, the box is considered intersecting. Why? Well, it is possible that none of the corners are inside the frustum itself but yet intersecting. In fact, consider the case where the frustum is contained entirely within the box. In this case, none of the points are inside the frustum but yet the box would still be considered visible.

Testing if a point is within the frustum is a simple procedure. All we need to do is to compare it to all 6 planes to make sure that it is on the front side of all of them (remember, all our planes face inwards into the frustum). Classifying a point relative to a plane is the same procedure we used in the sphere intersection method. We simply dot the point with the normal of the plane and then add the D component of the plane to that. If the value is greater than 0, then we are on the front of the plane. If it is less than 0, we are behind the plane. A value of 0 means that we are on the plane. Unless you have a specific purpose for classifying a point as on the plane or not, I wouldn抰 worry about it. I would simply use greater or equal to 0 when checking if we are on the front of the plane. (If you do have a reason for classifying a point as on the plane, then remember to NOT compare floats for equality but rather subtract them and check if the absolute value of that is less than some epsilon value). I won抰 bother to rewrite the method that I used in the sphere code but rest assured it抯 the same. Here is my method for comparing if a box is within the frustum or not:


                        // tests if a AaBox is within the frustrum
                        int Frustrum::ContainsAaBox(const AaBox& refBox) const
                        {
                        Vector3f vCorner[8];
                        int iTotalIn = 0;

	// get the corners of the box into the vCorner array
                        	refBox.GetVertices(vCorner);

	// test all 8 corners against the 6 sides
                        	// if all points are behind 1 specific plane, we are out
                        	// if we are in with all points, then we are fully in
                        	for(int p = 0; p < 6; ++p) {
                        int iInCount = 8;
                        int iPtIn = 1;

		for(int i = 0; i < 8; ++i) {

			// test this point against the planes
                        			if(m_plane[p].SideOfPlane(vCorner[i]) == BEHIND) {
                        iPtIn = 0;
                        --iInCount;
                        }
                        }

		// were all the points outside of plane p?
                        		If(iInCount == 0)
                        return(OUT);

		// check if they were all on the right side of the plane
                        		iTotalIn += iPtIn;
                        }

	// so if iTotalIn is 6, then all are inside the view
                        	if(iTotalIn == 6)
                        return(IN);

	// we must be partly in then otherwise
                        	return(INTERSECT);
                        }


We now have all the tools necessary to do frustum culling. So far so good right?


Optimizations 1


The first optimization for the above methods is very straightforward. If you study the two intersection methods you will most unquestionably notice that the sphere intersection method is significantly faster than the box intersection method. What this means is that we should perform sphere checks either instead of the box methods or at least before we check the box methods. In certain cases having a box as a bounding volume around our object can be much better since it will fit it more tightly. In these cases I would first check the bounding sphere of the object and then the bounding box. In fact, in my current engine each of my objects contains both a bounding sphere and a bounding box. The same goes for each node of my quad-tree. This way I can quickly reject objects/nodes using the sphere first and only if it passes that test do I check the box method. This is a very undemanding optimization and worth doing. All it requires is storing both a bounding sphere and box in each node/object that will be frustum culled.

The next optimization has to do with correctly traversing your hierarchal structure. In the case of the quad-tree the general method is to start at the top node and check if it抯 visible. If it is, then we then proceed to check each of the children of that node. If it is not visible, then we can stop processing. This is a recursive process for each node of the box. Once we reach the end of the tree and determine that this particular end node is visible, we send its contents to the video card for rendering. Now consider a non-terminating node (a node that contains children). If this node is completely visible, then what is the purpose of checking if the children are visible? It will only be wasted cpu cycles spent determining something you already know and that is that they are certainly visible! It is basically the opposite of not proceeding any further once you realize that the node isn抰 visible. In these cases, do not check further nodes but simply add them for rendering. The only case where you need to cull children nodes/objects is when the parent node is intersecting the frustum. This can significantly reduce your culling tests and eliminate trivial and redundant work.

The third optimization is to not check for an intersection if the camera is within the bound volume. In a case such as this we know that the bound volume intersects the frustum. We should check this node抯 children however since as I抳e said previously. For this check I merely check if the camera position is within the bounding box of this node, and if so treat it exactly as if the node is intersecting the viewing frustum. Using these optimizations, this is basically how your recursive processing method of your quad-tree should look:


                        // recursively process the node for objects to farm out to it抯 managers
                        void QuadTree::RecurseProcess(Camera* pPovCamera, QuadNode* pNode, bool bTestChildren)
                        {
                        // do we need to check for clipping?
                        	If(bTestChildren) {

		// check if we are inside this box first?		if(pNode->m_bbox.ContainsPoint(pPovCamera->Position()) == NOT_INSIDE) {

			// test the sphere first
                        			switch(pPovCamera->Frustrum().ContainsSphere(pNode->m_sphere)) {
                        case OUT:
                        return;
                        case IN:
                        bTestChildren = false;
                        break;
                        case INTERSECT:
                        // check if the box is in view
                        				switch(pPovCamera->Frustrum().ContainsAaBox(pNode->m_bbox)) {
                        case IN:
                        bTestChildren = false;
                        break;
                        case OUT:
                        return;
                        }
                        break;
                        }
                        }
                        }
                        // we can now check the children or render this node? Etc
                        }


Fundamental Methods 2


If you抳e already implemented all the previously mentioned material and profiled you application you may have noticed that the intersection code is still occupying a fairly large percentage of your cpu. Of course this depends on your application as well as the number of objects, the depth of your quad-tree, and various other factors. Even without profiling you have probably noticed that the intersection methods are fairly intensive. Even the fastest method of testing the sphere against the frustum requires testing each and every sphere against the 6 planes of the frustum, assuming no quick-outs. There are some improvements to be made. Before I get into them lets check out the methods that we will need in order to perform them.

The first is a sphere-sphere intersection test. This is a very easy and fast method to implement. Basically the code computes the distance between the centers of the spheres and if this distance is less than the sum of the radii of the spheres, then we have an intersection. Otherwise we don抰. Here is the method that I use for determining if two spheres intersect. Notice how I use the squared radius values instead of computing the squared root for the length between the centers? This speeds up this method appreciably.


                        // tests if 憈his?sphere intersects refSphere
                        bool Sphere::Intersects(const Sphere& refSphere) const
                        {
                        // get the separating axis
                        	Vector3f vSepAxis = this->Center() - refSphere.Center();

	// get the sum of the radii
                        	float fRadiiSum = this->Radius() + refSphere.Radius();

	// if the distance between the centers is less than the sum
                        	// of the radii, then we have an intersection
                        	// we calculate this using the squared lengths for speed
                        	if(vSepAxis.getSqLength() < (fRadiiSum * fRadiiSum))
                        return(true);

	// otherwise they are separated
                        	return(false);
                        }


The next method is to determine if a sphere and a cone intersect. This is a bit more involved method than the sphere-sphere check. Again, I could explain it but luckily for us both there is a great document by Dave Eberly explaining it on his site Magic-Software.com. The link to this article is:

http://www.magic-software.com/Documentation/IntersectionSphereCone.pdf

I find this site to be a great source of information, both on documents and on code. I highly recommend it to everyone. While the information in this article is more involved than what I presented so far, it surely isn抰 hard to understand and it抯 very easy and quick to implement. In fact, if you are math deprived then you can simply skip the end of the document and use the method provided as is. I don抰 recommend this but some people have a thing against math. So now we have these two dandy methods just sitting there... but what the heck are they used for you may ask? Well, that抯 the next section...


Optimizations 2


Yep, you guessed it. Those last two methods are used for a couple supplementary optimizations. As I mentioned at the beginning of the last section, doing checks against the frustum can be quite costly so it抯 best to avoid them if possible. You抣l notice that the sphere-sphere intersection test and the sphere-cone intersection tests are quite a bit zippier than the frustum intersection methods. So we can put those to use as a first level culling method to reduce the number of cull calls sent to the slower methods. What we need to do is to construct both a sphere and a cone around the current frustum. Then we can check our bounding spheres against this frustum sphere and then the frustum cone to grossly reject objects that are just plainly out of view. This is a very fast method (or methods) and depending on the layout of your world can result in some nice speed improvements.



Constructing a sphere around the frustum isn抰 that hard but it is more work than constructing the cone oddly enough. What we want with the sphere is to have it situated in the middle of the frustum with a radius that extends from the center of the sphere to a far corner of the frustum. Why the far corner? Well, the frustum 憇preads out?as you get further away from the camera and occupies more world space. The greatest distance then from the center of the sphere is to this far corner (there are 4 of them). We need to use this greatest distance as the radius of the sphere in order to correctly bound the frustum (see Figure 3). Calculating the center of the sphere is a effortless procedure. It is simply half way between the near and far clipping planes along the view vector of the camera starting at the camera position. Calculating the radius of this sphere is a little more involved. Usually a frustum is specified with a field of view (FOV) in radians. Using a bit of trigonometry and given the fact that we should know the distance from the far clipping plane to the near clipping plane, we can calculate the spread of the view frustum at it抯 maximum distance from the camera. We do this for both the x and y extents and use the far clipping distance as our z coordinate, calling this point Q. We then calculate the length from this point Q to the point P which is defined as (0, 0, nearClip + ((farClip ?nearClip) / 2)). This forms the radius of the sphere. Here is the code that I use to calculate this:


                        // calculate the radius of the frustum sphere
                        float fViewLen = m_fFarPlane - m_fNearPlane;

// use some trig to find the height of the frustum at the far plane
                        float fHeight = fViewLen * tan(m_fFovRadians * 0.5f);

// with an aspect ratio of 1, the width will be the same
                        float fWidth = fHeight;

// halfway point between near/far planes starting at the origin and extending along the z axis
                        Vector3f P(0.0f, 0.0f, m_fNearPlane + fViewLen * 0.5f);

// the calculate far corner of the frustum
                        Vector3f Q(fWidth, fHeight, fViewLen);

// the vector between P and Q
                        Vector3f vDiff(P - Q);

// the radius becomes the length of this vector
                        m_frusSphere.Radius() = vDiff.getLength();

// get the look vector of the camera from the view matrix
                        Vector3f vLookVector;
                        m_mxView.LookVector(&vLookVector);

// calculate the center of the sphere
                        m_frusSphere.Center() = m_vCameraPosition + (vLookVector * (fViewLen * 0.5f) + m_fNearPlane);


Constructing the cone that surrounds the frustum is much simpler. If you read the previous paper then you understand that the cone is basically defined by a vertex (origin of the cone), an axis ray (facing direction of the cone) and an angle that defines the expansion of the cone. The vertex of the cone is the position of the camera. The axis ray of the cone is the facing direction of the camera. The only consideration with the cone is the calculation of the cone angle. If we choose the cone angle to be the same as the field of view of the frustum, then we create a cone that cuts off the corners of the frustum. Picture the biggest circle that fits inside a box. So we need to create the cone angle such that it encompasses the corners of the frustum instead of just the sides. Using a bit of trigonometry we can calculate this new FOV. Since we have the FOV for the frustum, we can use this (and the dimensions of the screen) to calculate the adjacent side of the triangle. Then we can calculate the distance from the center of the screen to a corner. Using these two sides of a right triangle, we can then calculate the new FOV. Simple! Constructing the cone then is purely a matter of copying these properties into the cone itself. Here is my code for doing just that:


                        // set the properties of the frustum cone?vLookVector is the look vector from the view matrix in the
                        // camera.  Position() returns the position of the camera.
                        // fWidth is half the width of the screen (in pixels).
                        // fHeight is half the height of the screen in pixels.
                        // m_fFovRadians is the FOV of the frustum.
                        
                        // calculate the length of the fov triangle
                        float fDepth  = fHeight / tan(m_fFovRadians * 0.5f);

// calculate the corner of the screen
                        float fCorner = sqrt(fWidth * fWidth + fHeight * fHeight);

// now calculate the new fov
                        float fFov = atan(fCorner / fDepth);

// apply to the cone
                        m_frusCone.Axis() = vLookVector;
                        m_frusCone.Vertex() = Position();
                        m_frusCone.SetConeAngle(fFov);


Having constructed this sphere and cone we can use these to quickly reject objects/nodes based on the intersection (or lack thereof) between their bounding spheres and this frustum sphere/cone. (You抣l notice that I don抰 bother to cull nodes that are beyond the end of the cone. The reason is that these nodes are culled by the sphere stage itself. The cone serves the purpose of better culling nodes that lie to the sides of the frustum.) These checks are so quick that I always perform them as the first step in my culling. Incorporating them into the quad-tree traversal method of Part 3 leads us to this new process:


                        // recursively process the nodes of the quad tree
                        void QuadTree::RecurseProcess(Camera* pPovCamera, QuadNode* pNode, bool bTestChildren) {
                        // do we need to check for clipping?
                        	if(bTestChildren) {
                        // check if we are inside this box first...
                        		if(pNode->m_bbox.ContainsPoint(pPovCamera->Position()) == NOT_INSIDE) {

			// check if we are in the sphere of the frustum
                        			if(!pPovCamera->FrustrumSphere().Intersects(pNode->m_sphere))
                        return;
                        // check if we are in the cone of the frustum
                        			if(!TestConeSphereIntersect(pPovCamera->FrustumCone(), pNode->m_sphere))
                        return;

			// test the bounding sphere first
                        			switch(pPovCamera->Frustrum().ContainsSphere(pNode->m_sphere)) {
                        case OUT:
                        return;
                        case IN:
                        bTestChildren = false;
                        break;
                        case INTERSECT:
                        // check if the bound box is in view
                        				switch(pPovCamera->Frustrum().ContainsAaBox(pNode->m_bbox)) {
                        case IN:
                        bTestChildren = false;
                        break;
                        case OUT:
                        return;
                        }
                        break;

			}
                        }

	}

// we can now check the children or render this node? Etc
                        }


Conclusion


This pretty much sums up a good introduction to frustum culling that I hope many newbie engine programmers will find practical and helpful. As you can see by reading this, none of the concepts are hard and the math is very simple. There are of course many more optimizations that can be done to further enhance the culling procedure but this should serve as a good starting point. If anything sounds vague in the document, please let me know and I抣l try to write an update to clarify.

I would like to thank Gil Gribb and Klaus Hartmann for their excellent article on plane extraction. I would also like to thank Dave Eberly for his excellent resources for this cone/sphere intersection description as well as the full site he maintains. It has been an invaluable resource to me as I抦 sure it has been for many other programmers as well. I would also like to thank Charles Bloom for his web page that first inspired me to try enclosing the frustum in both a sphere and a cone. I feel really dumb for not thinking of it myself but that抯 the beauty of sharing information.

And remember... Go vegan and exercise like hell - it WILL make you smarter or your money back. I guarantee it (not a guarantee).

posted on 2009-03-26 10:57 狂烂球 阅读(3644) 评论(0)  编辑 收藏 引用 所属分类: 图形编程


只有注册用户登录后才能发表评论。
网站导航: 博客园   IT新闻   BlogJava   博问   Chat2DB   管理