感觉以前很少接触到这种划分的问题,但是它又好像很经典的样子。
本题要求划分的 k 块之间尽量一样。使他们的平均偏差最小。 可以很容易想到o(n^2)的dp。然后经队友提醒,采用单调队列优化到o(n)。o(n^2)的dp可以这样考虑:当第 i 根划分线紧跟在坐标 j 之后时, 枚举第 i-1 根划分线在前面的哪个位置然后转移。 要把这个dp降一维,首先要去掉绝对值。可以通过分类讨论来去掉绝对值。
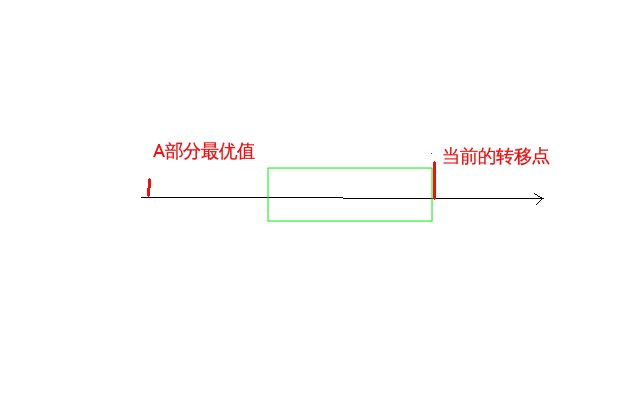
可以想像有一个滑动窗口(绿色),窗口内的转移项始终保持最后一项小于平均值。那么窗口左边的就始终大于平均值。这样绝对值就去掉了。然后维护一个滑动窗口里的单调队列就可以了。
1 #include <string>
2 #include <vector>
3 #include <map>
4 #include <cstdlib>
5 #include <cstring>
6 #include <cassert>
7 #include <set>
8 #include <iostream>
9 #include <sstream>
10 #include <cstddef>
11 #include <algorithm>
12 #include <utility>
13 #include <iterator>
14 #include <numeric>
15 #include <list>
16 #include <complex>
17 #include <cstdio>
18 #include <climits>
19 #include <cassert>
20
21
22 using namespace std;
23
24 const int maxn = 100100;
25
26 int gcd(int a, int b){return b ? gcd(b, a%b) : a; }
27
28 int X[maxn], Y[maxn], V[maxn];
29 int dp[12][maxn];
30
31 int N, K;
32
33 int que[maxn], bb, ee;
34 int minx, nowx;
35
36 void init()
37 {
38 minx = -1;
39 nowx = 0;//最小的当前仍然满足和 < N的下标
40 bb = 0;
41 ee = 0;
42 }
43
44 int solve(int X[])
45 {
46 sort(X, X + N);
47
48 V[0] = 0;
49 int cnt = 1, pre = -1;
50 for(int i = 0; i < N; i++)
51 {
52 if(X[i] == pre)
53 V[cnt-1]++;
54 else
55 {
56 V[cnt++] = 1;
57 pre = X[i];
58 }
59 }
60
61 //V[0]不是实际的点,是临时加的点
62 for(int i = 1; i < cnt; i++)
63 {
64 V[i] += V[i-1];
65 }
66
67 for(int i = 0; i < cnt; i++)
68 {
69 V[i] *= K; // 扩大倍数,没有分母
70 }
71
72 for(int i = 0; i < cnt; i++)
73 {
74 dp[1][i] = abs(V[i] - N);
75 }
76
77
78 for(int i = 2; i <= K; i++)
79 {
80 init();
81 for(int j = 0; j < cnt; j++)
82 {
83 while(V[j] - V[nowx] >= N)
84 {
85 if(minx==-1 || dp[i-1][minx] + V[nowx] - V[minx]> dp[i-1][nowx])
86 minx = nowx;
87 nowx++;
88 }
89
90 while(bb != ee && que[bb] < nowx)bb = (bb+1)%maxn;
91
92 while(bb != ee)
93 {
94 int lastid = ( ee - 1 + maxn ) % maxn;
95 int last = que[lastid];
96 if(dp[i-1][last] - ( V[j] - V[last]) < dp[i-1][j] )break;
97 ee = lastid;
98 }
99 que[ee] = j;
100 ee = ( ee + 1 ) % maxn;
101
102 assert(bb != ee);
103
104 dp[i][j] = dp[i-1][que[bb]] + N - ( V[j] - V[que[bb]] );
105
106 if(minx != -1)
107 dp[i][j] = min( dp[i][j], dp[i-1][minx] + V[j] - V[minx] - N );
108 }
109 }
110
111 return dp[K][cnt-1];
112 }
113
114 int main()
115 {
116 int cas = 1;
117 while(scanf("%d %d",&N, &K) != EOF)
118 {
119 if(N == 0 && K == 0)break;
120 for(int i = 0; i < N; i++)
121 {
122 scanf("%d %d",&X[i], &Y[i]);
123 }
124
125 int n = min( solve(X), solve(Y) );
126 int d = K*K;
127 int g = gcd(n, d);
128 printf("%d. %d/%d\n",cas++, n / g, d / g);
129 }
130 }
posted on 2010-07-18 16:21
wangzhihao 阅读(261)
评论(0) 编辑 收藏 引用 所属分类:
单调队列