一般来说,投影意味着降维操作,有一种投影方法是在某个方向上用0作为缩放因子。这种情况下,所有点都被拉平至垂直的轴(2D)或平面(3D)上。这种类型的投影称作正交投影(或者平行投影),因为从原来的点到投影点的直线相互平行。
向坐标轴或平面投影
最简单的投影方式是向坐标轴(2D)或平面(3D)投影,如图8.15所示:
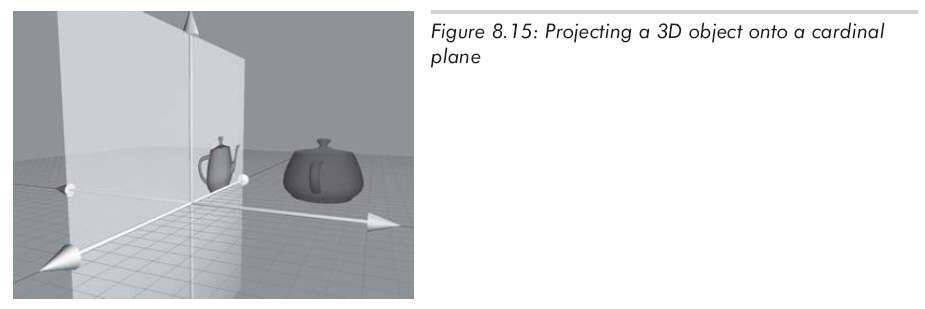
向坐标轴或平面投影在实际变换中不常发生,大多数情况是向低维的变换赋值,且要抛弃维数时。例如,将3D点赋值给2D点,抛弃z分量,只复制x和y。
通过使垂直方向上的缩放因子为零,就能向坐标轴或平面投影。考虑到完整性,下面列出这些变换矩阵,见公式8.10 -
8.14。

向任意直线或平面投影
也能向任意直线或平面投影,像往常一样,由于不考虑平移,这些直线或平面必须通过原点。投影由垂直于直线或平面的单位向量n定义。
通过使该方向的缩放因子为0能够导出向任意方向投影的矩阵,2D中的情况如公式8.15所示:
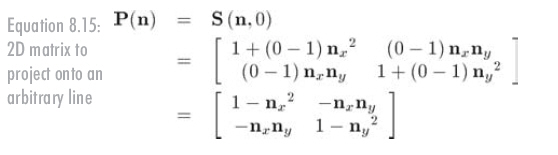
记住这里n垂直于投影直线,而不是平行。3D中,向垂直于n的平面投影的矩阵如公式8.16所示:
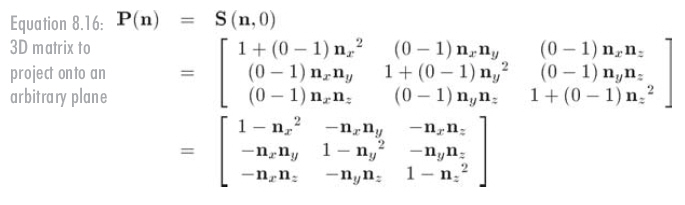
镜像
镜像(也叫做反射)是一种变换,其作用是将物体沿直线(2D中)或平面(3D中)“翻折”,图8.16展示了镜像的效果。
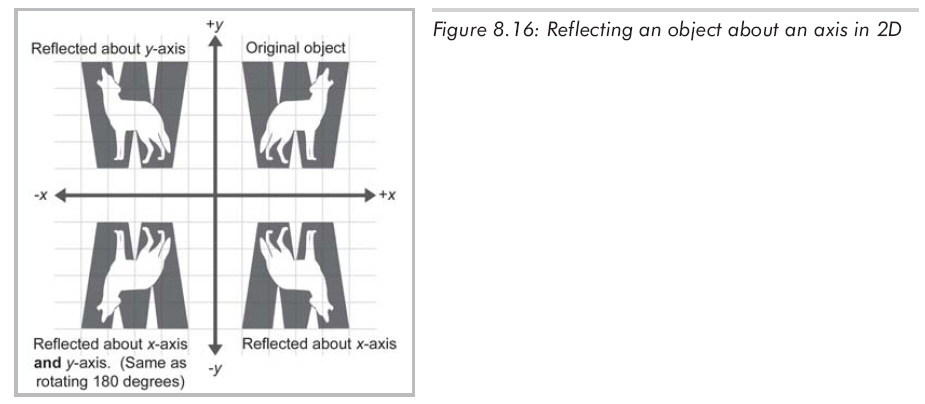
使缩放因子为-1能够很容易地实现镜像变换,设n为2D单位向量,公式8.17所示的矩阵将沿通过原点且垂直于n的反射轴来进行镜像变换。
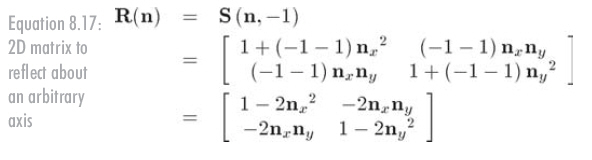
3D中,用反射平面代替直线。公式8.18中的矩阵将沿通过原点且垂直于n的平面来进行镜像变换:
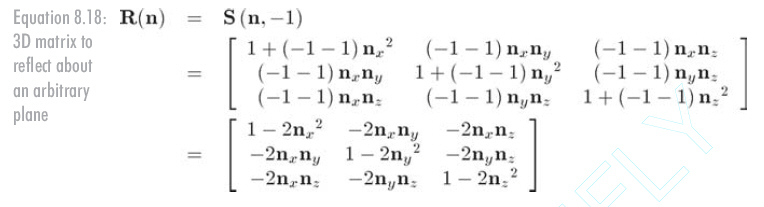
注意一个物体只能“镜像”一次,如果再次镜像(当沿不同的轴或平面的时候),物体将翻回“正面”(用一张纸来想象),这和在原位置旋转物体的效果一样。
切变
切变是一种坐标系“扭曲”变换,非均匀地拉伸它。切变的时候角度会发生变化,但令人惊奇的是面积和体积却保持不变。基本思想是将某一坐标的乘积加到另一个上。例如,2D中将y乘以某个因子然后加到x上,得到
x' = x + sy,如图8.17所示:
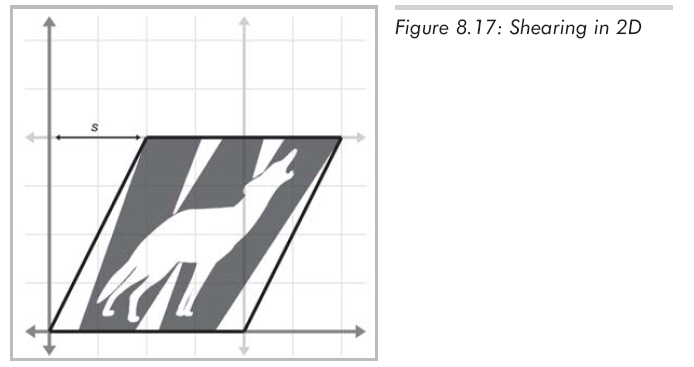
实现这个切变变换的矩阵为:
