4D向量和4x4矩阵不过是对3D运算的一种方便的记忆而已。
4D齐次空间
4D向量有4个分量,前3个是标准的x,y和z分量,第4个是w,有时称作齐次坐标。
为了理解标准3D坐标是怎样扩展到4D坐标的,让我们先看一下2D中的齐次坐标,它的形式为(x, y, w)。想象在3D中w=1处的标准2D平面,实际的2D点(x,
y)用齐次坐标表示为(x, y, 1),对于那些不在w=1平面上的点,则将它们投影到w=1平面上。所以齐次坐标(x,
y, w) 映射的实际2D点为(x/w, y/w)。如图9.2所示:

因此,给定一个2D点(x, y),齐次空间中有无数多个点与之对应。所有点的形式都为(kx, ky,
k),k≠0。这些点构成一条穿过齐次原点的直线。
当w=0时,除法未定义,因此不存在实际的2D点。然而,可以将2D齐次点(x, y, 0)解释为"位于无穷远的点",它描述了一个方向而不是一个位置。
4D坐标的基本思想相同,实际的3D点被认为是在4D中w=1"平面"上。4D点的形式为(x,
y, z, w),将4D点投影到这个"平面"上得到相应的实际3D点(x/w,
y/w, z/w)。w=0时4D点表示"无限远点",它描述了一个方向而不是一个位置。
4 X 4 平移矩阵
3x3变换矩阵表示的是线性变换,不包括平移。因为矩阵乘法的性质,零向量总是变换成零向量。因此,任何能用矩阵乘法表达的变换都不包含平移。这很不幸,因为矩阵乘法和它的逆是一种非常方便的工具,不仅可以用来将复杂的变换组合成简单的单一变换,还可以操纵嵌入式坐标系间的关系。如果能找到一种方法将3x3变换矩阵进行扩展,使它能处理平移,这将是一件多么美妙的事情啊。4x4矩阵恰好提供了一种数学上的"技巧",使我们能够做到这一点。
暂时假设w总是等于1。那么,标准3D向量[x, y, z]对应的4D向量为[x, y, z, 1]。任意3x3变换矩阵在4D中表示为:
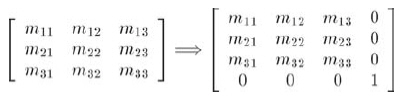
任意一个形如[x, y, z, 1]的向量乘以上面形式的矩阵,其结果和标准的3x3情况相同,只是结果是用w=1的4D向量表示的:
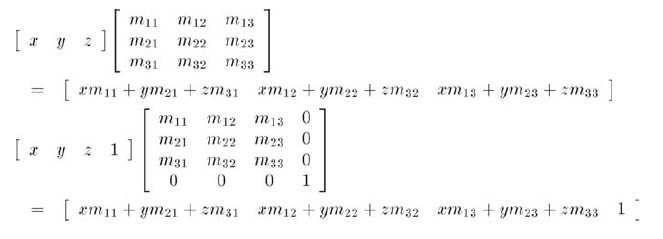
现在,到了最有趣的部分。在4D中,仍然可以用矩阵乘法来表达平移,如公式9.10所示,而在3D中是不可能的:
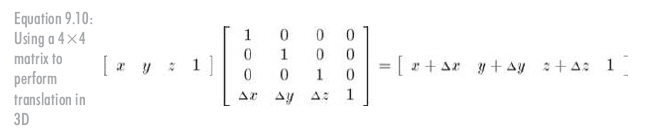
记住,即使是在4D中,矩阵乘法仍然是线性变换。矩阵乘法不能表达4D中的"平移",4D零向量也将总是被变换成零向量。这个技巧之所以能在3D中平移点是因为我们实际上是在切变4D空间。与实际3D空间相对应的4D中的"平面"并没有穿过4D中的原点。因此,我们能通过切变4D空间来实现3D中的平移。
设想没有平移的变换后接一个有平移的变换会发生什么情况呢?设R为旋转矩阵(实际上,R还能包含其他的3D线性变换,但现在假设R只包含旋转),T为形如公式9.10的变换矩阵:
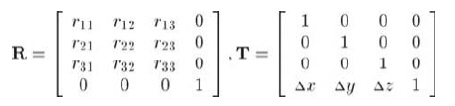
将向量v先旋转再平移,新的向量v'计算如下:
v' = vRT
注意,变换的顺序是非常重要的。因为我们使用的是行向量,变换的顺序必须和矩阵乘法的顺序相吻合(从左到右),先旋转后平移。
和3x3矩阵一样,能将两个矩阵连接成单个矩阵,记作矩阵M,如下:
M = RT
v' = vRT = v(RT) = vM
观察M的内容:
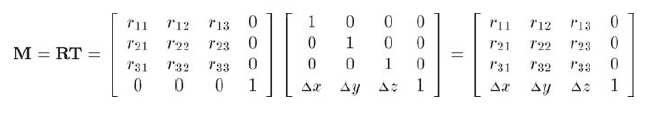
注意到,M的上边3x3部分是旋转部分,最下一行是平移部分。最右一列为[0, 0, 0,
1]T。逆向利用这些信息,能将任意4x4矩阵分解为线性变换部分和平移部分。将平移向量[△x,
△y, △z]记作t,则M可简写为:
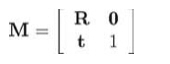
接下来看w=0所表示的 "无穷远点"。它乘以一个由"标准"3x3变换矩阵扩展成的4x4矩阵(不包含平移),得到:
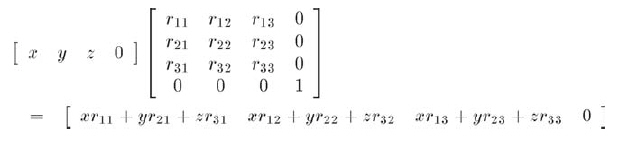
换句话说,当一个形如[x, y, z,
0]的无穷远点乘以一个包含旋转、缩放等的变换矩阵,将会发生预期的变换。结果仍是一个无穷远点,形式为[x, y, z, 0]。
一个无穷远点经过包含平移的变换可得到:
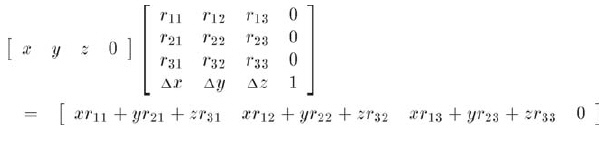
注意到结果是一样的(和没有平移的情况相比)。换句话说,4D向量中的w分量能够"开关"
4x4 矩阵的平移部分。这个现象是非常有用的,因为有些向量代表“位置”,应当平移,而有些向量代表“方向”,如表面的法向量,不应该平移。从几何意义上说,能将第一类数据当作"点",第二类数据当作"向量".
使用4x4矩阵的一个原因是4x4变换矩阵能包含平移。当我们仅为这个目的使用4x4矩阵时,矩阵的最后一列总是[0,
0, 0, 1]T。既然是这样,为什么不去掉最后一列而改用4x3矩阵呢?根据线性代数法则,由于多种原因,4x3矩阵不符合我们的需求,如下:
(1)不能用一个4x3矩阵乘以另一个4x3矩阵。
(2)4x3矩阵没有逆矩阵,因为它不是一个方阵。
(3)一个4D向量乘以4x3矩阵时,结果是一个3D向量。
为了严格遵守线性代数法则,我们加上了第4列。当然在代码中,可以不受代数法则的约束。