特殊的2D直线表示方法
2D中,可以使用公式12.3隐式表示直线:
ax + by = d
公式12.3 2D直线的隐式定义
另一种表示方法为,设向量n = [a, b],用向量记法将公式12.3写为公式12.4的形式:
p . n = d
公式12.4 用向量记法的2D直线的隐式定义
当等式两边同乘以常数k时,n和d会发生变化但这并不会改变直线的定义。如果n为单位向量,大多数情况下计算会很方便。
再换一种表示方法,变换等式,将直线表示为斜截式,见公式12.5:
y = mx + b
公式12.5 斜截式
m是直线的"斜率",等于rise和run的比值:每向上移动rise单位,就会向右移动run单位。b是y截距(不同于第一种隐式法中的b)。b之所以称为y截距,是因为直线和y轴相交于此。将x=0代入上述等式,就可以清楚地看出直线和y轴交于y=b。如图12.5所示:
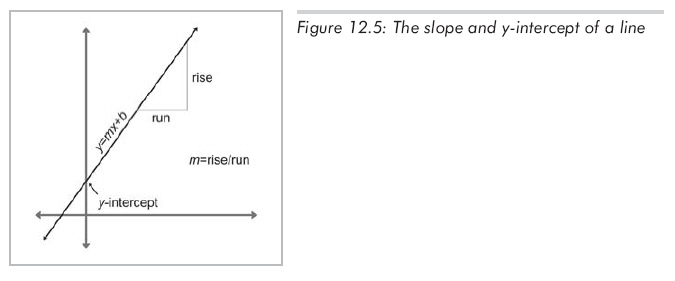
水平直线的斜率为0,竖直直线的斜率为无穷大,不能用斜截式表示。竖直直线的隐式表示为:
x = k
另一种描述直线的方法是给出垂直于直线的标准向量n和原点到直线的垂直距离d。标准向量描述了直线的方向,距离则描述了直线的位置。如图12.6所示:

注意,这只是公式12.4的一种特殊情况。n是垂直于直线的单位向量,d给出了原点到直线的有符号距离。这个距离是在垂直于直线的方向(平行于n)上度量的。有符号距离的意思是如果直线和标准向量n代表的点在原点的同一侧,则d为正。当d增大时,直线沿方向n移动。
一种变形是用直线上的点来描述直线的位置而不是用原点到直线的距离。当然,直线上的任意点都可以。直线的方向仍然用垂直于直线的标准向量n表示,如图12.7所示:
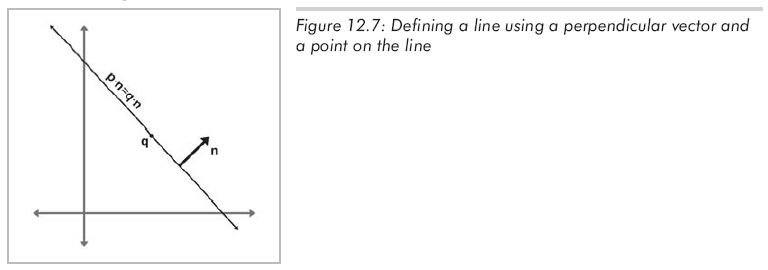
最后一种定义是将直线作为两个点q和r的垂直平分线,如图12.8所示。事实上,这也是直线最早的一种定义:到两个给定点距离相等的点的集合。
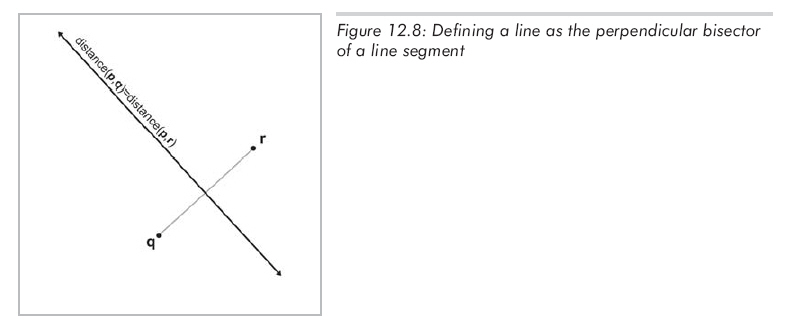
在不同表示方法间转换
注意,直线的表示方法仅适用于2D。
从射线的两点定义式转换到参数形式:
p0 = porg
d = pend - porg
相反的转换,从参数形式转换到两点定义的形式:
porg = p0
pend = p0 + d
如果给定一条射线的参数形式,就能够从中计算出包含该射线的直线的隐式表示:
a = dy
b = -dx
d = porgdy - porgdx
直线的隐式转换到斜截式:
m = -a/b,b = d/b
注意,等号左边的b是斜截式 ---- y = mx + b中的b;等号右边的b则是隐式ax
+ by = d中y的系数。
从直线的隐格式转换到"标准向量 + 距离"形式:
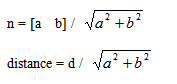
从"标准向量 + 直线上的点"形式转换到"标准向量
+ 距离"形式(设n为标准向量):
n = n
distance = n . q
最后,从垂直平分线形式转换到隐格式:
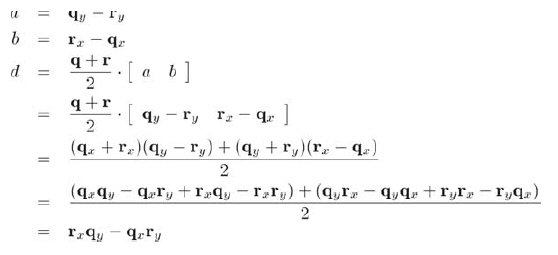
球和圆
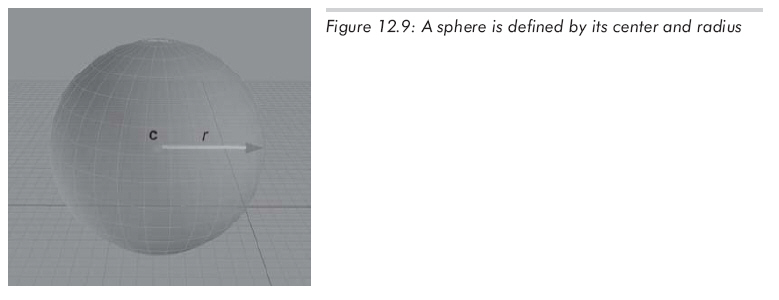
球是一种3D物体,定义为到给定点的距离为给定长度的所有点的集合。球面上某点到球心的距离称作球的半径,球的直接表示形式能描述出球心c和半径r,如图12.9所示:
球的简单性使它在计算几何和图形学中几乎无处不在。"边界球"经常用于相交性测试中,因为检验与一个球是否相交是非常简单的。而且由于旋转一个球时并不会改变它的形状,所以使用边界球时不必考虑物体的方向。
由球的定义可以直接导出它的隐式表示形式:到球心的距离为给定距离的点的集合。球心为c,半径为r的球的隐式表示形式为:
|| p - c || = r
公式12.6 向量记法的球的隐式表示
注意p是球表面上的任意一点。如果要让球内部的点p也满足这个式子,就必须将等号换为"≤"。公式12.6也是2D圆的隐式表示,将公式12.6在3D中展开,两边同时平方得到公式12.7:
(x - cx)2 + (y - cy)2
+ (z - cz)2 = r2
公式12.7 球的隐式定义
我们能计算圆和球的直径(经过圆心的直线与圆有两个交点,这两个交点间的距离称作直径)和周长(绕圆一周的长度即为周长),见公式12.8:
D = 2r
C = 2πr = πD
公式12.8 圆的直径和周长
公式12.9为圆的面积:
A = πr2
公式12.9 圆面积
球的表面积S及体积V的计算方式如公式12.10所示:
S = 4πr2
V = 4/3 πr3
公式12.10 球的表面积和体积
如果学过微积分,你会发现一个非常有趣的现象:圆面积的微分是圆周长,球体积的微分是球表面积。