相交性测试的目的是检测两个几何图元是否相交,在某些情况下还要求出相交部分,这些基本测试构成了碰撞检测系统的基础。碰撞检测用来防止物体互相穿越,或者使物体看起来好像互相被弹开。
我们将讨论两种不同类型的相交性测试:
(1)静态测试检测两个静止图元是否相交。它是一种布尔型测试----也就是说,测试结果只有真(相交时)或假(不相交时)。如果两个图元相交,则可以获取更多的信息。但一般来说,这种测试的目的只是返回一个布尔值。
(2)动态测试针对的是两个运动图元,检测它们是否相交,及相交的时间点,运动值通常以参数形式来表达。因此,这种测试返回的结果不仅仅是一个布尔型的真/假值,还会返回一个指明相交时间点的值(参数t的值)。对于这里我们要讨论的测试,运动值是一个简单的线性位移---当t从0变化到1时原向量的偏移值。每个图元都可以有自己的运动值,然而,从单个图元的角度来考虑问题会比较简单。也就是说,一个图元被认为是静止的,同时另一个图元做了所有的运动。很容易做到这一点,只要将两个位移向量组合成一个相对位移向量,它描述了两个图元间的相对移动关系。因此,所有动态测试总是涉及一个静态图元和一个动态图元。
注意,包含射线在内的许多重要的测试实际上都是动态测试,因为射线能被看作一个运动的图元。
在2D中两条隐式直线的相交性检测
在2D中,要检测用隐式定义的两条直线是否相交是非常简单的,通过解线性方程组就能解决问题。
我们有两个方程(两条直线的隐式方程)和两个未知数(交点的x、y坐标)。两个方程分别为:
a1x + b1y = d1
a2x + b2y = d2
解此方程组得公式13.5:
x = (b2d1 - b1d2) / (a1b2
- a2b1)
y = (a1d2 - a2d1) / (a1b2
- a2b1)
公式13.5 计算2D中两直线的交点
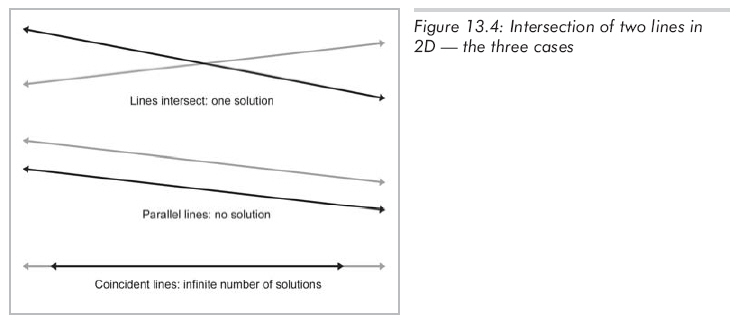
和其他方程组一样,存在3中可能性(如图13.4所示):
(1)只有一个解,这种情况下,公式13.5中的分母为非0值。
(2)无解,意味着直线是平行的,永远不会相交,分母为0。
(3)无穷多解,意味着两条直线重合,分母为0。
在3D中两条射线的相交性检测
考虑3D中两条以参数形式定义的射线:
r1(t1) = p1 + t1d1
r2(t2) = p2 + t2d2
我们能够解得它们的交点。暂时先不考虑t1、t2的取值范围。因此我们考虑的是无限长的射线,同样向量d1、d2也不必是单位向量。如果这两条射线在一个平面中,那么也存在三种可能性:
(1)两条射线交于一点。
(2)两条射线平行,没有交点。
(3)两条射线重合,有无限多交点。
在3D中,还有第四种可能性,两条射线不在一个平面中,如图13.5所示:
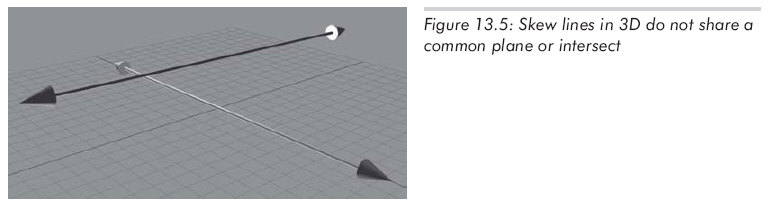
下面演示如何解得交点处的t1、t2:

如果两条射线平行或重合,d1、d2的叉乘为0,所以上面两个等式的分母为0。如果两条射线不在一个平面内,那么p1(t1)和p2(t2)是相距最近的点。通过检查p1(t1)和p2(t2)间的距离即可确定两条射线相交的情况。当然在实践中因为浮点数的精度问题,精确的相交很少出现,这时就需要用到一个偏差值。
上面的讨论假设没有限定t1、t2的取值范围,如果射线的长度有限(或只沿一个方向延伸),在计算出t1、t2后还应做适当的边界检测。
射线和平面的相交性检测
在3D中射线与平面相交于一点,射线的参数定义为:
p(t) = p0 + td
平面以标准方式来定义,即对于平面上的所有点p,都满足:
p . n = d
尽管n和d都被限制为单位向量,但这里是没有必要加上这些限制条件的(如图13.6):
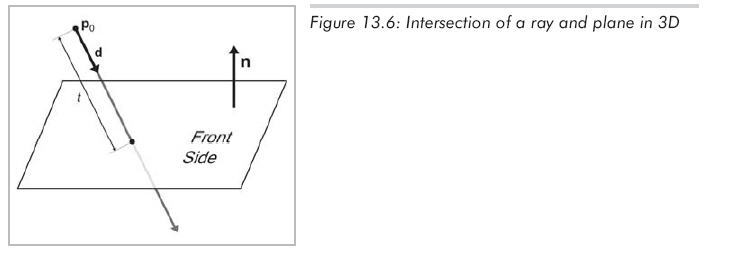
解得相交点的t值,暂时假设射线的长度是无限的(公式13.6):
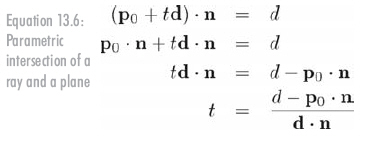
如果射线和平面互相平行,分母d . n
为0,则它们之间没有交点。(我们仅讨论与平面的正面相交的情况,在这种情况下,仅当射线的方向和平面的法向量相反时才有交点,此时d .
n < 0)。如果t超出了取值范围,说明射线和平面不相交。